人教版八年级数学 下册 16.3 二次根的加减 课件(2课时,共38张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 16.3 二次根的加减 课件(2课时,共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 15:39:00 | ||
图片预览










文档简介
(共38张PPT)
强者能同命运的风暴抗争。
—— 爱迪生
16.3 二次根式的加减
人教版八年级数学 下册
目标导航
1.探索二次根式加减运算的法则。
2.会进行二次根式的加减运算。
3.能根据运算律和相关法则进行二次根式的四则运算。
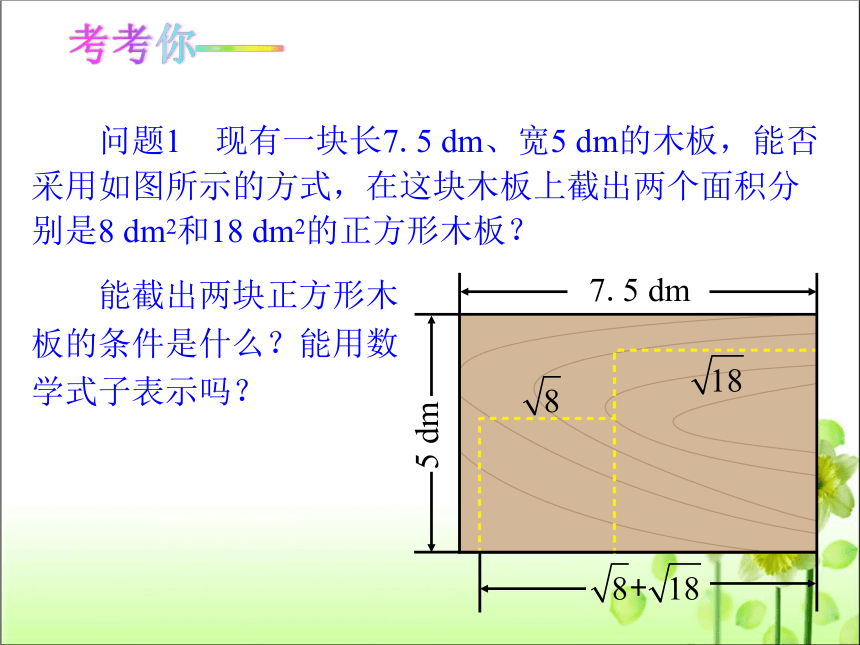
问题1 现有一块长7.5 dm、宽5 dm的木板,能否
采用如图所示的方式,在这块木板上截出两个面积分
别是8 dm2和18 dm2的正方形木板?
能截出两块正方形木
板的条件是什么?能用数
学式子表示吗?
5 dm
7.5 dm
考考你——
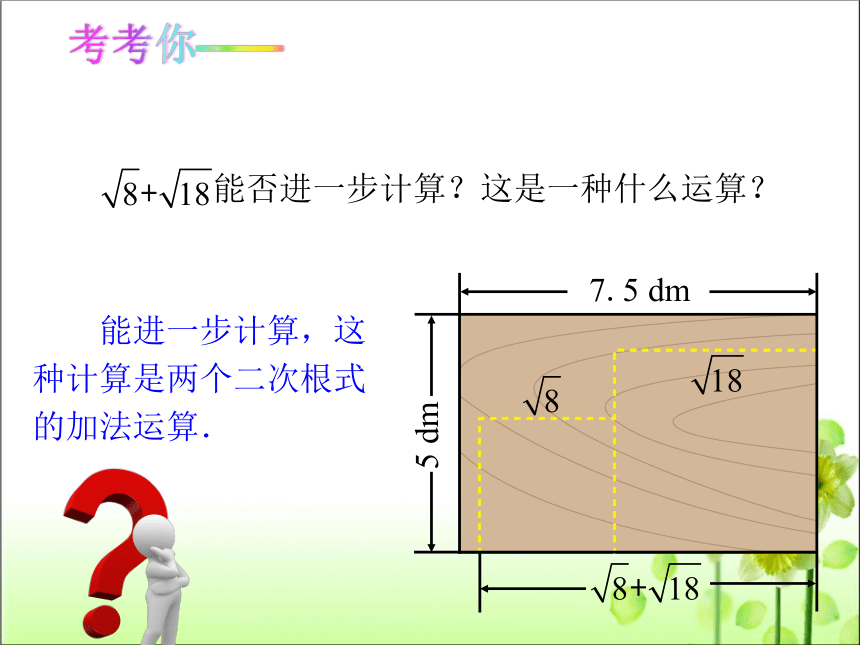
能否进一步计算?这是一种什么运算?
能进一步计算,这
种计算是两个二次根式
的加法运算.
5 dm
7.5 dm
考考你——
认真阅读课本第12至13页的内容,完成下面练习并体验知识点的形成过程.
自主学习
问题 怎样计算 ?
如果看不出 能否化简,我们不妨把问题简
化,先看算式 能否化简.
用分配
律合并
整式
加减
你能得到这样的两个二次根式加减的方法吗?
将同类二次根式用分配律合并.
合作探究
算式 与算式 有什么相同点与不同
点?
请化简算式 ,并说出每一步化简的理由.
化为最简
二次根式
用分配
律合并
整式
加减
合作探究
二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
合作探究
二次根式加减法法则:
√
√
×
×
1. 判断下列计算是否正确?为什么?
(1)
(3)
(2)
(4)
即学即练
2.下面与 是同类二次根式的是( )
A. B.
C. D.
C
你答对了吗
即学即练
知识点二 二次根式的加减法法则和运算
上面的问题中,利用________律将 和 进行合并.由此得,二次根式的加减法法则:二次根式加减时,可以先将二次根式化成______________ ,再将 ____________的二次根式进行_______.
分配
最简二次根式
被开方数相同
合并
合作探究
例1 计算:
⑴ ; ⑵
解:⑴ 原式=
(化成______ 二次根式)
= ( 律)
= (合并)
最简
分配
4
3
⑵
解:(2)原式=
=
=
计算(1) ;
(2) .
解:⑴原式= =
⑵原式=
=
=
例2 计算:(1) ;
(2) .
解:⑴ 原式=
= (化简二次根式)
= (合并)
22
3
42
化简后被开方数_______的二次根式(同类二次根式)才能合并,因此
______合并(填能或不能)
相同
不能
1、下列计算是否正确?为什么?
⑴ ;
⑵ ;
⑶ ;
⑷ .
解:⑴⑵不正确,
不能化简.
⑶正确.
⑷不正确,2
与 不能合并.
即学即练
2、计算:
(1)
解:⑴原式=
=
(2)
解:原式=
=
(3)
解:原式=
=
=
3、如图,两个圆的圆心相同,它们的面积分别是12.56和25.12.求圆环的宽度d( 取3.14,
结果保留小
数点后两位).
解:
答:圆环的宽度d约为0.83.
d=
=
=
=
≈0.83
你答对了吗
1、二次根式加减时,可以先将二次根式化成_______________,再将____________
的二次根式进行________ .
2、化简后被开方数_______的二次根式(同类二次根式)才能合并,否则不能合并.
最简二次根式
被开方数相同
合并
相同
归纳小结
例1 计算:
(1)
(2)
思考:(1)中,先计算什么?后计算什么,最后
的目标是什么?(2)呢?
合作探究
与有理数、实数运算一样,在混合运算中先乘除,
后加减;
对于(1):先算乘,再化简,若有相同的二次根
式进行合并,最后的目标是二次根式是最简二次根式;
对于(2):先算除,再化简,若有相同的二次根
式进行合并,把所有的二次根式化成最简二次根式.
合作探究
例1 计算:
解:
(1)
思考:(1)中,每一步的依据是什么?
第一步的依据是:分配律或多项式乘单项式;
第二步的依据是:二次根式乘法法则;
第三步的依据是:二次根式化简.
(1)
(2)
合作探究
解:
例1 计算:
(2)
思考:(2)中,每一步的依据是什么?
第一步的依据是:多项式除以单项式法则;
第二步的依据是:二次根式除法法则.
(1)
(2)
合作探究
例2 计算:
解:
(1)
思考:(1)中,每一步的依据是什么?
第一步的依据是:多项式乘多项式法则;
第二步的依据是:二次根式化简,合并被开方数
相同的二次根式(依据是:分配律);
第三步的依据是:合并同类项.
(1)
(2)
合作探究
解:
例2 计算:
(2)
思考1:(2)中,每一步的依据是什么?
每一步的依据是:平方差公式.
思考2:为什么二次根式运算中可以用运算律?
乘法公式使计算准确、简便,因此能用运算公式
的,尽可能用运算公式.因为二次根式表示数,二次
根式的运算也是实数的运算.
(1)
(2)
合作探究
解:原式=
= - = __
5
3
2
以上运用了 公式.
平方差
温馨提示:
在二次根式的运
算中,
__________
法则和
公式仍然适用.
多项式乘以多项式
乘法公式
6
练习1 计算:
(1)
(2)
练习2 计算 的结果是
( ).
A
A.
B.
C.
D.
即学即练
练习3 化简: .
解:原式
即学即练
多项式乘除法法则和乘法公式在 运算中同样适用.
二次根式的混合
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教材中相关练习题。
强者能同命运的风暴抗争。
—— 爱迪生
16.3 二次根式的加减
人教版八年级数学 下册
目标导航
1.探索二次根式加减运算的法则。
2.会进行二次根式的加减运算。
3.能根据运算律和相关法则进行二次根式的四则运算。
问题1 现有一块长7.5 dm、宽5 dm的木板,能否
采用如图所示的方式,在这块木板上截出两个面积分
别是8 dm2和18 dm2的正方形木板?
能截出两块正方形木
板的条件是什么?能用数
学式子表示吗?
5 dm
7.5 dm
考考你——
能否进一步计算?这是一种什么运算?
能进一步计算,这
种计算是两个二次根式
的加法运算.
5 dm
7.5 dm
考考你——
认真阅读课本第12至13页的内容,完成下面练习并体验知识点的形成过程.
自主学习
问题 怎样计算 ?
如果看不出 能否化简,我们不妨把问题简
化,先看算式 能否化简.
用分配
律合并
整式
加减
你能得到这样的两个二次根式加减的方法吗?
将同类二次根式用分配律合并.
合作探究
算式 与算式 有什么相同点与不同
点?
请化简算式 ,并说出每一步化简的理由.
化为最简
二次根式
用分配
律合并
整式
加减
合作探究
二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
合作探究
二次根式加减法法则:
√
√
×
×
1. 判断下列计算是否正确?为什么?
(1)
(3)
(2)
(4)
即学即练
2.下面与 是同类二次根式的是( )
A. B.
C. D.
C
你答对了吗
即学即练
知识点二 二次根式的加减法法则和运算
上面的问题中,利用________律将 和 进行合并.由此得,二次根式的加减法法则:二次根式加减时,可以先将二次根式化成______________ ,再将 ____________的二次根式进行_______.
分配
最简二次根式
被开方数相同
合并
合作探究
例1 计算:
⑴ ; ⑵
解:⑴ 原式=
(化成______ 二次根式)
= ( 律)
= (合并)
最简
分配
4
3
⑵
解:(2)原式=
=
=
计算(1) ;
(2) .
解:⑴原式= =
⑵原式=
=
=
例2 计算:(1) ;
(2) .
解:⑴ 原式=
= (化简二次根式)
= (合并)
22
3
42
化简后被开方数_______的二次根式(同类二次根式)才能合并,因此
______合并(填能或不能)
相同
不能
1、下列计算是否正确?为什么?
⑴ ;
⑵ ;
⑶ ;
⑷ .
解:⑴⑵不正确,
不能化简.
⑶正确.
⑷不正确,2
与 不能合并.
即学即练
2、计算:
(1)
解:⑴原式=
=
(2)
解:原式=
=
(3)
解:原式=
=
=
3、如图,两个圆的圆心相同,它们的面积分别是12.56和25.12.求圆环的宽度d( 取3.14,
结果保留小
数点后两位).
解:
答:圆环的宽度d约为0.83.
d=
=
=
=
≈0.83
你答对了吗
1、二次根式加减时,可以先将二次根式化成_______________,再将____________
的二次根式进行________ .
2、化简后被开方数_______的二次根式(同类二次根式)才能合并,否则不能合并.
最简二次根式
被开方数相同
合并
相同
归纳小结
例1 计算:
(1)
(2)
思考:(1)中,先计算什么?后计算什么,最后
的目标是什么?(2)呢?
合作探究
与有理数、实数运算一样,在混合运算中先乘除,
后加减;
对于(1):先算乘,再化简,若有相同的二次根
式进行合并,最后的目标是二次根式是最简二次根式;
对于(2):先算除,再化简,若有相同的二次根
式进行合并,把所有的二次根式化成最简二次根式.
合作探究
例1 计算:
解:
(1)
思考:(1)中,每一步的依据是什么?
第一步的依据是:分配律或多项式乘单项式;
第二步的依据是:二次根式乘法法则;
第三步的依据是:二次根式化简.
(1)
(2)
合作探究
解:
例1 计算:
(2)
思考:(2)中,每一步的依据是什么?
第一步的依据是:多项式除以单项式法则;
第二步的依据是:二次根式除法法则.
(1)
(2)
合作探究
例2 计算:
解:
(1)
思考:(1)中,每一步的依据是什么?
第一步的依据是:多项式乘多项式法则;
第二步的依据是:二次根式化简,合并被开方数
相同的二次根式(依据是:分配律);
第三步的依据是:合并同类项.
(1)
(2)
合作探究
解:
例2 计算:
(2)
思考1:(2)中,每一步的依据是什么?
每一步的依据是:平方差公式.
思考2:为什么二次根式运算中可以用运算律?
乘法公式使计算准确、简便,因此能用运算公式
的,尽可能用运算公式.因为二次根式表示数,二次
根式的运算也是实数的运算.
(1)
(2)
合作探究
解:原式=
= - = __
5
3
2
以上运用了 公式.
平方差
温馨提示:
在二次根式的运
算中,
__________
法则和
公式仍然适用.
多项式乘以多项式
乘法公式
6
练习1 计算:
(1)
(2)
练习2 计算 的结果是
( ).
A
A.
B.
C.
D.
即学即练
练习3 化简: .
解:原式
即学即练
多项式乘除法法则和乘法公式在 运算中同样适用.
二次根式的混合
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教材中相关练习题。
