人教版八年级数学 下册 17.1 勾股定理 课件(3课时,共54张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 17.1 勾股定理 课件(3课时,共54张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 15:42:54 | ||
图片预览








文档简介
(共54张PPT)
没有哪门学科能比数学更为清晰地阐明自然界的和-谐性。
——卡罗斯
17.1 勾股定理
人教版八年级数学 下册
目标导航
1.经历勾股定理的探究过程,归纳勾股定理内容。
2.能用勾股定理解决一些简单问题,证明直角三角形全等的“斜边、直角边”判定定理。
3.体会勾股定理在数学中的地位和作用。
目标导航一
认 识勾 股 定 理
国际数学家大会是最高水平的全球性数学科学学术
会议.2002年在北京召开了第24届国际数学家大会.如
图就是大会的会徽的图案.
问题1 你见过这个图案吗?
它由哪些基本图形组成?
趣味数学
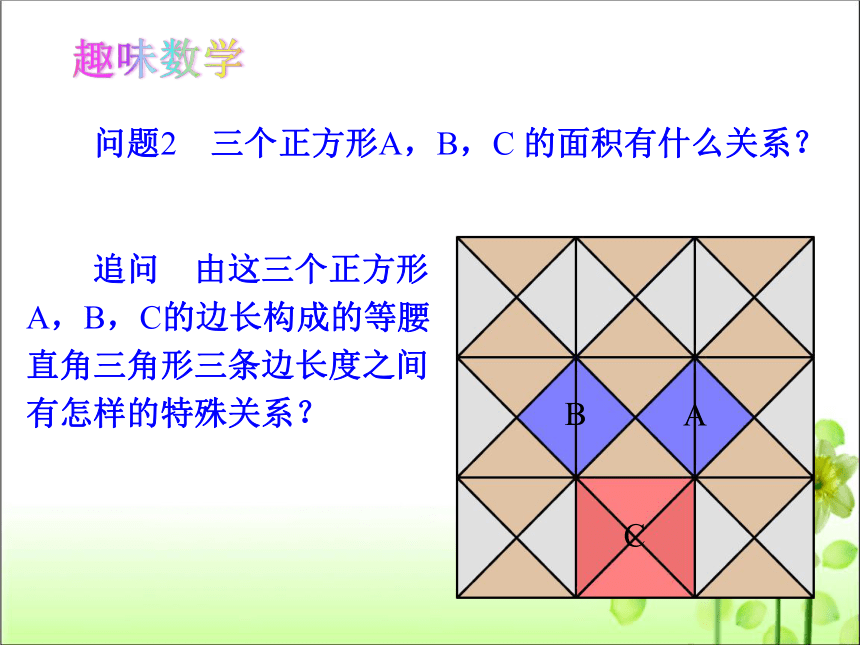
追问 由这三个正方形
A,B,C的边长构成的等腰
直角三角形三条边长度之间
有怎样的特殊关系?
问题2 三个正方形A,B,C 的面积有什么关系?
A
B
C
趣味数学
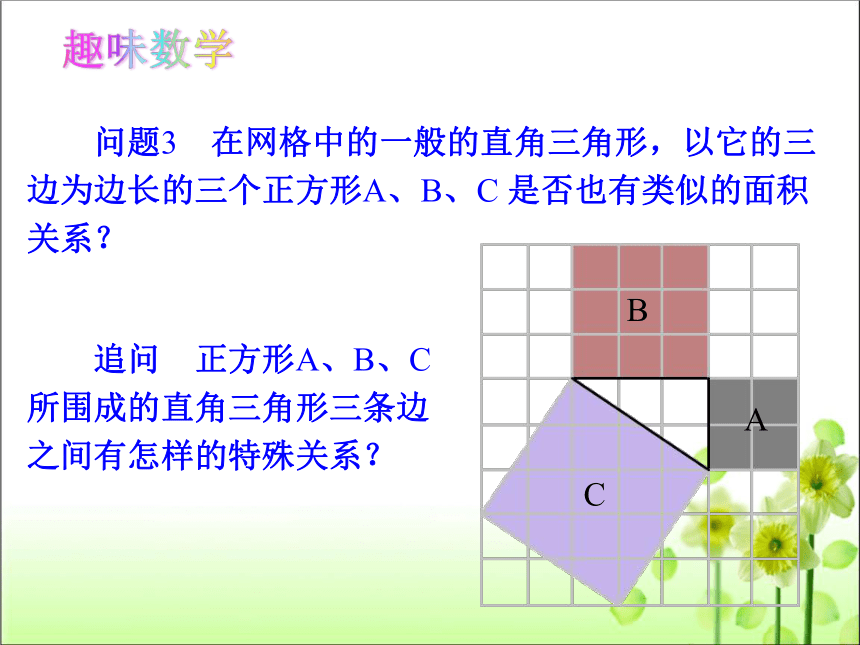
追问 正方形A、B、C
所围成的直角三角形三条边
之间有怎样的特殊关系?
问题3 在网格中的一般的直角三角形,以它的三
边为边长的三个正方形A、B、C 是否也有类似的面积
关系?
A
B
C
趣味数学
问题4 通过前面的探究活动,猜一猜,直角三角形三边之间应该有什么关系?
趣味数学
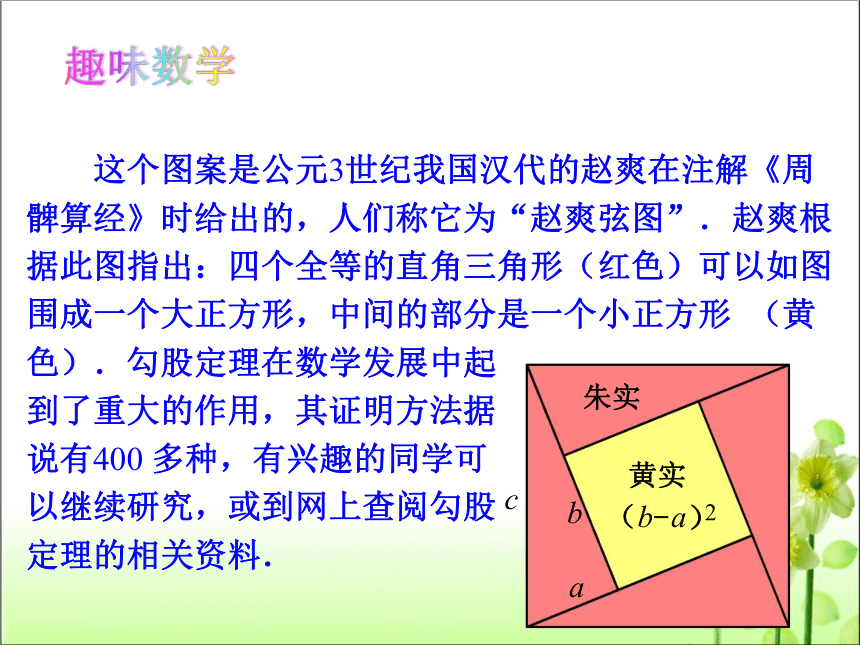
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究,或到网上查阅勾股
定理的相关资料.
c
b
a
(
b
-
a
)
2
黄实
朱实
趣味数学
认真阅读课本第22页到第24页的内容,完成下面练习并体验知识点的形成过程。
广东省怀集县马宁镇初级中学 徐志才
自主研学
知识点一 勾股定理的探究
1、如图,邮票图案的三个
正方形小方格中间是一个直
角三角形,如果1个小方格
为1个单位面积,那么直角
三角形的两直角边长分别是
____和____,
斜边长是____;
三个正方形的面积分别是_____、_____和____.
4
3
5
16
9
25
合作探究
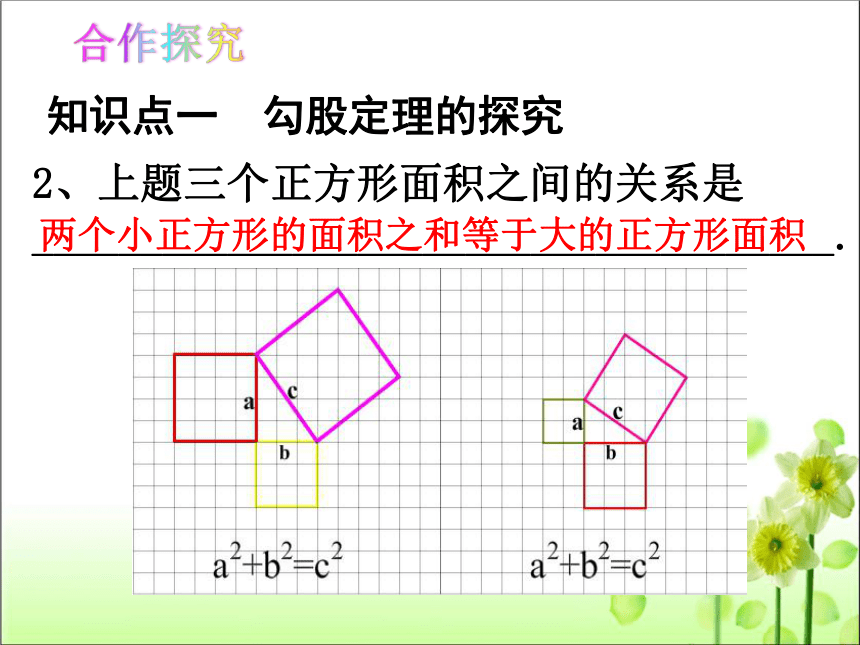
2、上题三个正方形面积之间的关系是
_____________________________________.
两个小正方形的面积之和等于大的正方形面积
知识点一 勾股定理的探究
合作探究
知识点一 勾股定理的探究
3、把上题三个正方形的面积关系,转化为直角三角形三边的关系,则得到什么结论?
结论:直角三角形两直角边的 __ _____
等于 .
?
命题1(勾股定理) 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
平方和
斜边的平方
a2+b2=c2
合作探究
1、判断题
(1)若a、b、c是三角形的三边,则 . ( )
(2)直角三角形中,两边的平方和等于第三边 的平方. ( )
×
×
即学即练
2、 求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
知识点二 勾股定理的证明
1、赵爽弦图利用了_______关系进行勾股定理的证明.
2、剪4个全等的直角三角形,拼成如图图形,其中直角三角形的两直角边分别是a、b,则中间的小正方形的边长为________,利用面积证明勾股定理.
面积
b-a
合作探究
∵ S大正方形
=4S直角三角形+S小正方形
=4×_______+(____)2
=___________________
=___________________
又∵S大正方形=C2
∴______2+______2=_______2
b-a
2ab+b2-2ab+a2
a2 +b2
a
b
C
知识点二 勾股定理的证明
合作探究
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A、B、C、D的边长分别是12,16,9,12,求最大正方形E的面积.
A
B
C
D
E
H
F
K
G
即学即练
解:如图所示
正方形A、B、C、D的边长分别是12,16,9,12,
设直角三角形的斜边长为c ,由勾股定理知
122+162=c2,c=20 ,即正方形F边长为20.
同理可得, 正方形G的边长为15
故直角三角形的两直角边分别为20,15.设它的斜边长为k,由勾股定理知
202+152=k2,k=25
正方形E的边长为25,S正方形E=25×25=625
1、勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
2、赵爽弦图利用了___ ____关系进行勾股定理的证明.
a2+b2=c2
面积
归纳小结
目标导航二
应用勾股定理求距离
已知一个直角三角形的两边,应用勾股定理可以求
出第三边,这在求距离时有重要作用.
勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边
长为c,那么a2+b2=c2.
认真阅读课本第25页的内容,完成下面练习并体验知识点的形成过程。
自主研学
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以
木板能从门框内通过.
将实际问题转化为数学问
题,建立几何模型,画出图形,分
析已知量、待求量,让学生掌握解
决实际问题的一般套路.
A
B
C
D
1 m
2 m
合作探究
1、如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A、B两点间的距离(结果取整数).
解:在Rt△ABC中,根据勾股定理得:
答:A、B两点间的距离约为57m
即时练习
例2.今有池方一丈,芦苇生其中央,出水一尺,引芦苇赴岸,适与岸齐.问水深、芦苇长各几何?
A
B
C
分析:
可设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52= ,
通过解方程可得.
合作探究
利用勾股定理解决实际问题
的一般思路:
(1)重视对实际问题题意的
正确理解;
(2)建立对应的数学模型,
运用相应的数学知识;
(3)方程思想在本题中的运
用.
A
B
C
例2.今有池方一丈,芦苇生其中央,出水一尺,引芦苇赴岸,适与岸齐.问水深、芦苇长各几何?
合作探究
株树之间的垂直距离是____米,水平距离是 米.
2、如图,山坡的坡角为30°,山坡上两株树木之间的坡面距离是
米,
则这两
6
即时练习
例3 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m.如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
O
B
D
CC
A
C
A
O
B
O
D
合作探究
解:在Rt△AOB中,根据勾股定理,
OB2=________=__________=___
OB=____=___
在Rt△COD中,根据勾股定理,
OD2=________=_______________=______
OD=_____≈______
BD=OD-OB≈_______=______.
所以______________________
____________________________________
3.15
1.77
1
AB2-OA2
2.62-2.42
1
CD2-OC2
2.62-(2.4-0.5)2
1.77-1
0.77
梯子的顶端下滑0.5m时,梯子底端
并不是也外移0.5m,而是外移0.77m.
3、一木杆在离地面3米处折断,木杆顶端落在离木杆底端4米处.木杆折断之前有多高?
解:依题意得,PR=3,PQ=4
在Rt△RPQ中,根据勾股定理,
RQ=
所以木杆折断之前高度为PR+RQ=3+5=8m
即时练习
4、如图,在平面直角坐标系中有两点(5,0)和B(0,4).求这两点之间的距离.
解:依题意得,OA=5,OB=4
在Rt△AOB中,根据勾股定理,
AB=
所以这两点之间的距离为
广东省怀集县永固镇初级中学 方慧吾
如果直角三形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
1、勾股定理:
__________________________________
_____________________
2、勾股定理有广泛的应用.
归纳小结
目标导航三
应用勾股定理证“HL”
问题1 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.
学习了勾股定理后,你能证明这一结论吗?
认真阅读课本第26至27页的内容,完成下面练习并体验知识点的形成过程.
知识点一 勾股定理的应用
已知:如图,在Rt△ABC和Rt△A'B'C' 中,∠C=∠C'=90°,AB=A'B',AC=A'C'.
求证:△ABC≌△A'B'C'.
自主研学
′
′
′
′
′
′
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
证明:在Rt△ABC 和
Rt△A B C 中,∠C=∠C′
=90°,根据勾股定理,得
′
′
′
A
B
C
A
B
C′
′
′
合作探究
A
B
C
A
B
C′
′
′
′
′
′
∴ △ABC≌△A B C
(SSS).
′
′
′
′
′
′
证明:
∵ AB=A B ,
AC=A C ,
∴ BC=B C .
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
合作探究
1、如图,等边三角形的边长是6,
求:(1)高AD的长;
(2)这个三角形的面积
解:(1)∵AD是等边三角形
ABC的高
∴AD平分∠BAC,∠BAC=30°
BD= AB=3
根据勾股定理:AD2=AB2-BD2
=62-32=27 ∴AD=
即学即练
(2)这个三角形的面积
解:
= AB.AD
= ×6×3
=9
2、如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2.
证明:∵ ∠ACB =∠ECD,
∴ ∠ACD +∠BCD=∠ACD +∠ACE ,
∴ ∠BCD =∠ACE.
又 BC=AC, DC=EC,
∴ △ACE≌△BCD.
A
B
C
D
E
即学即练
A
B
C
D
E
证明:∴ AE=DB,∠B =∠CAE=45°,
∠DAE =∠CAE+∠BAC
=45°+45°=90°.
∴ AD2 +AE2 =DE2.
∵ AE=DB ,
∴ AD2 +DB2 =DE2.
3、如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2.
即学即练
知识点二 在数轴上作出表示无理数的点
1、两条直角边都是1的直角三角形的斜边长=____;
2、直角三角形一直角边长是3,另一直角边长是2,那么它的斜边长=_______.
合作探究
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
作法:
(1)在数轴上找到点A,使OA=3;
(2)过点A作直线l垂直于OA,在l上取点B,使AB=2,那么OB=________;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC=________.
如图,在数轴上,点C为表示_______的点.
2、在数轴上作出表示 点
A
l
B
C
合作探究
4、利用勾股定理,可以作出长为 、 、
…的点.
作法与提示:
A
(1)在数轴上标记点A,经过点A作OA的垂线m
m
(2)在m上取点K,使AG=1,连接OG
G
(3)以O为圆心OG为半径作弧,弧与数轴交于点B,
则点B的坐标就是
B
(4)类似于作 的步骤,标出 和 的点
“数学海螺”
类比迁移
1、在数轴上作出表示 的点(不写作法).
作法与提示:
(1)在数轴上标记点4为点A,经过点A作OA的
垂线n
A
n
(2)在直线n上取一点B使得AB=1,连接OB
B
(3)以O为原点OB为半径作弧,弧与数轴交于点C,
则点C的坐标就是
C
即学即练
2、如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点,在图中画一个三角形,使它的三边分别为3, , .
作法与提示:
(1)在网格中,分别画出长度为3, , 的线
段,并如图标记点A、B、C、D
A
B
3
C
D
(2)以B为圆心,BC为半径作弧
以A为圆心,AD为半径作弧
(3)两弧交于点O,连接AO,BO
则△ABO就是所求三角形
O
即学即练
1、勾股定理的应用(HL);
2、如何在数轴上作出表示无理数的点.
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
没有哪门学科能比数学更为清晰地阐明自然界的和-谐性。
——卡罗斯
17.1 勾股定理
人教版八年级数学 下册
目标导航
1.经历勾股定理的探究过程,归纳勾股定理内容。
2.能用勾股定理解决一些简单问题,证明直角三角形全等的“斜边、直角边”判定定理。
3.体会勾股定理在数学中的地位和作用。
目标导航一
认 识勾 股 定 理
国际数学家大会是最高水平的全球性数学科学学术
会议.2002年在北京召开了第24届国际数学家大会.如
图就是大会的会徽的图案.
问题1 你见过这个图案吗?
它由哪些基本图形组成?
趣味数学
追问 由这三个正方形
A,B,C的边长构成的等腰
直角三角形三条边长度之间
有怎样的特殊关系?
问题2 三个正方形A,B,C 的面积有什么关系?
A
B
C
趣味数学
追问 正方形A、B、C
所围成的直角三角形三条边
之间有怎样的特殊关系?
问题3 在网格中的一般的直角三角形,以它的三
边为边长的三个正方形A、B、C 是否也有类似的面积
关系?
A
B
C
趣味数学
问题4 通过前面的探究活动,猜一猜,直角三角形三边之间应该有什么关系?
趣味数学
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究,或到网上查阅勾股
定理的相关资料.
c
b
a
(
b
-
a
)
2
黄实
朱实
趣味数学
认真阅读课本第22页到第24页的内容,完成下面练习并体验知识点的形成过程。
广东省怀集县马宁镇初级中学 徐志才
自主研学
知识点一 勾股定理的探究
1、如图,邮票图案的三个
正方形小方格中间是一个直
角三角形,如果1个小方格
为1个单位面积,那么直角
三角形的两直角边长分别是
____和____,
斜边长是____;
三个正方形的面积分别是_____、_____和____.
4
3
5
16
9
25
合作探究
2、上题三个正方形面积之间的关系是
_____________________________________.
两个小正方形的面积之和等于大的正方形面积
知识点一 勾股定理的探究
合作探究
知识点一 勾股定理的探究
3、把上题三个正方形的面积关系,转化为直角三角形三边的关系,则得到什么结论?
结论:直角三角形两直角边的 __ _____
等于 .
?
命题1(勾股定理) 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
平方和
斜边的平方
a2+b2=c2
合作探究
1、判断题
(1)若a、b、c是三角形的三边,则 . ( )
(2)直角三角形中,两边的平方和等于第三边 的平方. ( )
×
×
即学即练
2、 求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
知识点二 勾股定理的证明
1、赵爽弦图利用了_______关系进行勾股定理的证明.
2、剪4个全等的直角三角形,拼成如图图形,其中直角三角形的两直角边分别是a、b,则中间的小正方形的边长为________,利用面积证明勾股定理.
面积
b-a
合作探究
∵ S大正方形
=4S直角三角形+S小正方形
=4×_______+(____)2
=___________________
=___________________
又∵S大正方形=C2
∴______2+______2=_______2
b-a
2ab+b2-2ab+a2
a2 +b2
a
b
C
知识点二 勾股定理的证明
合作探究
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A、B、C、D的边长分别是12,16,9,12,求最大正方形E的面积.
A
B
C
D
E
H
F
K
G
即学即练
解:如图所示
正方形A、B、C、D的边长分别是12,16,9,12,
设直角三角形的斜边长为c ,由勾股定理知
122+162=c2,c=20 ,即正方形F边长为20.
同理可得, 正方形G的边长为15
故直角三角形的两直角边分别为20,15.设它的斜边长为k,由勾股定理知
202+152=k2,k=25
正方形E的边长为25,S正方形E=25×25=625
1、勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
2、赵爽弦图利用了___ ____关系进行勾股定理的证明.
a2+b2=c2
面积
归纳小结
目标导航二
应用勾股定理求距离
已知一个直角三角形的两边,应用勾股定理可以求
出第三边,这在求距离时有重要作用.
勾股定理:
如果直角三角形的两条直角边长分别为a,b,斜边
长为c,那么a2+b2=c2.
认真阅读课本第25页的内容,完成下面练习并体验知识点的形成过程。
自主研学
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以
木板能从门框内通过.
将实际问题转化为数学问
题,建立几何模型,画出图形,分
析已知量、待求量,让学生掌握解
决实际问题的一般套路.
A
B
C
D
1 m
2 m
合作探究
1、如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m.求A、B两点间的距离(结果取整数).
解:在Rt△ABC中,根据勾股定理得:
答:A、B两点间的距离约为57m
即时练习
例2.今有池方一丈,芦苇生其中央,出水一尺,引芦苇赴岸,适与岸齐.问水深、芦苇长各几何?
A
B
C
分析:
可设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52= ,
通过解方程可得.
合作探究
利用勾股定理解决实际问题
的一般思路:
(1)重视对实际问题题意的
正确理解;
(2)建立对应的数学模型,
运用相应的数学知识;
(3)方程思想在本题中的运
用.
A
B
C
例2.今有池方一丈,芦苇生其中央,出水一尺,引芦苇赴岸,适与岸齐.问水深、芦苇长各几何?
合作探究
株树之间的垂直距离是____米,水平距离是 米.
2、如图,山坡的坡角为30°,山坡上两株树木之间的坡面距离是
米,
则这两
6
即时练习
例3 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m.如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
O
B
D
CC
A
C
A
O
B
O
D
合作探究
解:在Rt△AOB中,根据勾股定理,
OB2=________=__________=___
OB=____=___
在Rt△COD中,根据勾股定理,
OD2=________=_______________=______
OD=_____≈______
BD=OD-OB≈_______=______.
所以______________________
____________________________________
3.15
1.77
1
AB2-OA2
2.62-2.42
1
CD2-OC2
2.62-(2.4-0.5)2
1.77-1
0.77
梯子的顶端下滑0.5m时,梯子底端
并不是也外移0.5m,而是外移0.77m.
3、一木杆在离地面3米处折断,木杆顶端落在离木杆底端4米处.木杆折断之前有多高?
解:依题意得,PR=3,PQ=4
在Rt△RPQ中,根据勾股定理,
RQ=
所以木杆折断之前高度为PR+RQ=3+5=8m
即时练习
4、如图,在平面直角坐标系中有两点(5,0)和B(0,4).求这两点之间的距离.
解:依题意得,OA=5,OB=4
在Rt△AOB中,根据勾股定理,
AB=
所以这两点之间的距离为
广东省怀集县永固镇初级中学 方慧吾
如果直角三形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
1、勾股定理:
__________________________________
_____________________
2、勾股定理有广泛的应用.
归纳小结
目标导航三
应用勾股定理证“HL”
问题1 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.
学习了勾股定理后,你能证明这一结论吗?
认真阅读课本第26至27页的内容,完成下面练习并体验知识点的形成过程.
知识点一 勾股定理的应用
已知:如图,在Rt△ABC和Rt△A'B'C' 中,∠C=∠C'=90°,AB=A'B',AC=A'C'.
求证:△ABC≌△A'B'C'.
自主研学
′
′
′
′
′
′
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
证明:在Rt△ABC 和
Rt△A B C 中,∠C=∠C′
=90°,根据勾股定理,得
′
′
′
A
B
C
A
B
C′
′
′
合作探究
A
B
C
A
B
C′
′
′
′
′
′
∴ △ABC≌△A B C
(SSS).
′
′
′
′
′
′
证明:
∵ AB=A B ,
AC=A C ,
∴ BC=B C .
已知:如图,在Rt△ABC 和Rt△A B C 中,∠C=
∠C =90°,AB=A B ,AC=A C .
求证:△ABC≌△A B C .
′
′
′
′
′
′
′
′
′
′
′
合作探究
1、如图,等边三角形的边长是6,
求:(1)高AD的长;
(2)这个三角形的面积
解:(1)∵AD是等边三角形
ABC的高
∴AD平分∠BAC,∠BAC=30°
BD= AB=3
根据勾股定理:AD2=AB2-BD2
=62-32=27 ∴AD=
即学即练
(2)这个三角形的面积
解:
= AB.AD
= ×6×3
=9
2、如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2.
证明:∵ ∠ACB =∠ECD,
∴ ∠ACD +∠BCD=∠ACD +∠ACE ,
∴ ∠BCD =∠ACE.
又 BC=AC, DC=EC,
∴ △ACE≌△BCD.
A
B
C
D
E
即学即练
A
B
C
D
E
证明:∴ AE=DB,∠B =∠CAE=45°,
∠DAE =∠CAE+∠BAC
=45°+45°=90°.
∴ AD2 +AE2 =DE2.
∵ AE=DB ,
∴ AD2 +DB2 =DE2.
3、如图,△ACB和△ECD都是等腰直角三角形,
∠ACB =∠ECD =90°,D为AB边上一点.求证:AD2 +
DB2 =DE2.
即学即练
知识点二 在数轴上作出表示无理数的点
1、两条直角边都是1的直角三角形的斜边长=____;
2、直角三角形一直角边长是3,另一直角边长是2,那么它的斜边长=_______.
合作探究
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
作法:
(1)在数轴上找到点A,使OA=3;
(2)过点A作直线l垂直于OA,在l上取点B,使AB=2,那么OB=________;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC=________.
如图,在数轴上,点C为表示_______的点.
2、在数轴上作出表示 点
A
l
B
C
合作探究
4、利用勾股定理,可以作出长为 、 、
…的点.
作法与提示:
A
(1)在数轴上标记点A,经过点A作OA的垂线m
m
(2)在m上取点K,使AG=1,连接OG
G
(3)以O为圆心OG为半径作弧,弧与数轴交于点B,
则点B的坐标就是
B
(4)类似于作 的步骤,标出 和 的点
“数学海螺”
类比迁移
1、在数轴上作出表示 的点(不写作法).
作法与提示:
(1)在数轴上标记点4为点A,经过点A作OA的
垂线n
A
n
(2)在直线n上取一点B使得AB=1,连接OB
B
(3)以O为原点OB为半径作弧,弧与数轴交于点C,
则点C的坐标就是
C
即学即练
2、如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点,在图中画一个三角形,使它的三边分别为3, , .
作法与提示:
(1)在网格中,分别画出长度为3, , 的线
段,并如图标记点A、B、C、D
A
B
3
C
D
(2)以B为圆心,BC为半径作弧
以A为圆心,AD为半径作弧
(3)两弧交于点O,连接AO,BO
则△ABO就是所求三角形
O
即学即练
1、勾股定理的应用(HL);
2、如何在数轴上作出表示无理数的点.
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
