人教版八年级数学 下册 17.2 勾股定理逆定理 课件(2课时,共45张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 17.2 勾股定理逆定理 课件(2课时,共45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 843.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 15:45:15 | ||
图片预览











文档简介
(共45张PPT)
社会犹如一条船,每个人都要有掌舵的准备.
—— 易卜生
17.2 勾股定理逆定理
人教版八年级数学 下册
目标导航
1.探究勾股定理的逆定理及二者关系。
2.得出逆命题的概念,知道原命题为真命题,它的逆命题不一定为真命题。
3.应用勾股定理的逆定理解决实际问题。
目标导航一
勾股定理逆定理
勾股定理 如果直角三角形的两条直角边长分别为
a,b,斜边长为c,那么a2+b2=c2.
题设(条件):直角三角形的
两直角边长为a,b,斜边长为c .
结论:a2+b2=c2.
问题1 回忆勾股定理的内容.
形
数
复习回顾
思考 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是否是直角三角形?
逆向思考
据说,古埃及人曾用下面的方法画直角:把一根长
绳打上等距离的13 个结,然后以3 个结间距,4 个结间
距、5 个结间距的长度为边长,用木桩钉成一个三角形,
其中一个角便是直角.你认为结论正确吗?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
如果三角形的三边分别
为3,4,5,这些数满足
关系:32+42=52,围成的
三角形是直角三角形.
逆向思考
(1)画一画:下列各组数中的两数平方和等于第三数的 平方,分别以这些数为边长画出三角形(单位:cm), 它们是直角三角形吗?
① 2.5,6,6.5; ② 6,8,10.
(2)量一量:用量角器分别测量上述各三角形的最大角 的度数.
(3)想一想:请判断这些三角形的形状,并提出猜想.
实验操作
A1
B1
C1
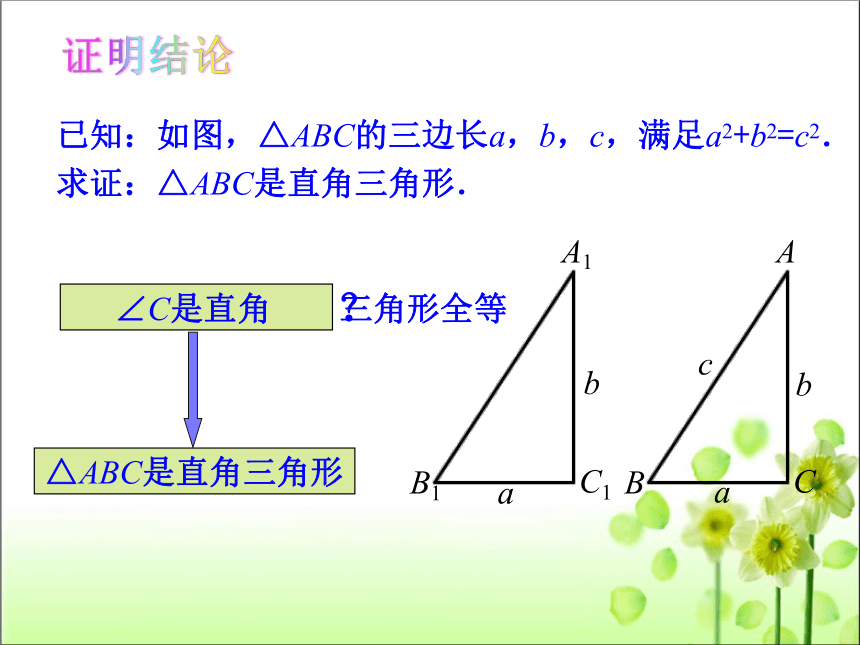
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
?
三角形全等
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
a
证明结论
作用:判定一个三角形三边满足什么条件时为直角三角形.
定理:如果三角形的三边长a,b,c 满足a2+b2=c2,
那么这个三角形是直角三角形.
形成定理
知识点一 勾股定理的逆定理
画△ABC,使①a=3cm,b=4cm,c=5cm;
②a=2.5cm,b=6cm,c=6.5cm;
③a=4cm,b=7.5cm,c=8.5cm.
以上a、b、c的关系都满足__________;
△ABC是________ 三角形.
a2+b2=c2
直角
认真阅读课本第31至32页的内容,完成下面练习并体验知识点的形成过程.
自主研学
知识点一 勾股定理的逆定理
结论:命题2(勾股定理的逆定理)
如果三角形的三边长a、b、c,满足 ,
那么这个三角形是 三角形.
直角
自主研学
如果三条线段长a、b、c满足 ,这三条线段组成的三角形是不是直角三角形?为什么?
解:
根据题意,因为三角形的三边长度a、b、c满足a2+b2=c2 ,则根据勾股定理的逆定理,这个三角形是直角三角形.
即学即练
知识点二 证明勾股定理的逆定理
已知:△ABC的三边长分别为a、b、c,且a2+b2=c2. 求证:∠C=90°.
合作探究
知识点二 证明勾股定理的逆定理
证明:作Rt△A′B′C′,使∠C′= 90°,B′C′= BC = a, A′C′= AC = b.
∵A'B'2=B'C'2+A'C'2= ________=____
∴A'B' =_______
在△ABC和△A'B'C'中
________________________
________________________
________________________
AB=A'B'
AC=A'C'
BC=B'C'
∴_________≌________(SSS)
∴∠C=_______=90°.
BC2+AC2
AB2
AB
∠ C'
△ABC
△ A'B'C'
合作探究
知识点三 勾股定理的逆定理的运用
例1 判断由线段a、b、c组成的三角形是不是直角三角形:(1)a=15,b=8,c=17.
(2)a=13,b=14,c=15.
解:(1)因为152+82= __________= _____
172=_____
所以 + = ,
根据________________,这三角形是直角三角形.注:像8,15,17这样能够成为_____________ ________的三个__ ____,称为勾股数
225+64
289
289
152
82
172
勾股定理的逆定理
直角三角形三
条边长
正整数
合作探究
知识点三 勾股定理的逆定理的运用
例1 判断由线段a、b、c组成的三角形是不是直角三角形:(1)a=15,b=8,c=17.
(2)a=13,b=14,c=15.
(2)因为132+142= ___________= _____
152=_____
所以 + ≠ ,
根据_______ _______,这个三角形不是直角三角形.
169+16
185
225
132
42
152
勾股定理的逆定理
合作探究
1、下列四组数中:
①1、、2;②32,42,52 ;③9,40,41;④3k、4k、5k(k为正整数).
属于勾股数的有__________(填序号).
③④
即学即练
(1)a=7,b=24,c=25(2)a= ,b=4,c=5
(3)a= ,b=1,c= (4)a=40,b=50,c=60.
解:(1)因为a2+b2=49+576=625,
c2=252=625 a2+b2=c2
所以,根据勾股定理的逆定理,
a、b、c组成的三角形是直角三角形
即学即练
2、判断由线段a、b、c组成的三角形是不是直角三角形:
(2)因为b2+c2=16+25=41, a2=41
b2+c2=a2
所以,根据勾股定理的逆定理,a、b、c组成的三角形是直角三角形
解:(3)因为c2+b2=
a2= , c2+b2=a2
所以,根据勾股定理的逆定理,a、b、c组成的三角形是直角三角形
解:(4)因为a2+b2=1600+2500=4100, c2=3600 , a2+b2≠c2
所以,根据勾股定理的逆定理,a、b、c组成的三角形不是直角三角形
勾股定理的逆定理:
定理:如果三角形的三边长a,b,c 满足a2+b2=c2,
那么这个三角形是直角三角形.
勾股定理:如果直角三角形两直角边分别为a,b,
斜边为c,那么a2+b2=c2.
归纳小结
正整数
能够成为直角三角形三条边长的三个____________,称为勾股数.
目标导航二
勾股定理逆定理的应用
1、命题1(勾股定理) 如果直角三角形的两
条直角边长分别为a,b,斜边长为c,那么
__________.
a2+b2=c2
2、命题2(勾股定理的逆定理)
如果三角形的三边长a、b、c,满足
那么这个三角形是 ___________ 三角形.
a2+b2=c2
直角
理论梳理
认真阅读课本第31至33页的内容,完成下面练习并体验知识点的形成过程.
原命题、逆命题和逆定理
自主研学
1、上面命题1与命题2的题设和结论正好______.像这样的两个命题叫做_____,命题;如果把其中一个叫做原命题,那么另一个叫做它的__________.
相反
互逆
逆命题
2、一般地,原命题成立时,它的逆命题
既可能成立,也可能不成立.如果一个定理
的逆命题经过证明是_______________,
那么它也是一个定理,我们称这两个定理
互为逆定理.
正确的
合作探究
定理与逆定理
我们已经学习过哪些互逆的定理?
(1)任何一个命题都有逆命题;
原命题与逆命题的关系是题设和结论相互转换
(2)原命题正确,逆命题不一定正确;原命题不正确,逆命题可能正确。
(3)一个定理未必有逆定理。
(1)等腰三角形的两底角相等
原命题:如果一个三角形是等腰三角形,那么这个三角形的两底角相等。
逆命题:如果一个三角形的两底角相等,那么这个三角形是等腰三角形。
写出下列命题的逆命题并判断它们是否成立:
(2)两直线平行,同位角相等
原命题:如果两条直线平行,那么同位角相等。
逆命题:如果同位角相等,那么两直线平行。
(3)三内角之比为1:2:3的三角形为
直角三角形
原命题:如果一个三角形三内角之比为1:2:3,
那么这个三角形是直角三角形。
逆命题:如果一个三角形是直角三角形,
那么这个三角形三内角之比为1:2:3。
1、说出下列命题的逆命题.这些逆命题
成立吗?
⑶全等三角形的对应角相等;
⑷在角的内部,到角的两边距离相等的点
在角的平分线上.
答:逆命题为:对应角相等的三角形全等 。
不成立
答:逆命题为:在角平分线上的点到角的两
边距离相等。 成立
即学即练
说出下列命题的逆命题.这些命题的逆命题是真命
题吗?
(1)两条直线平行,内错角相等;
逆命题:内错角相等,两直线平行.真命题.
(2)对顶角相等;
逆命题:相等的角是对顶角.假命题.
(3)线段垂直平分线上的点到线段两端点的距离相等.
逆命题:到线段两端点的距离相等的点在线段的
垂直平分线上.真命题.
任何一个命题都有逆
命题;原命题是真命题,其
逆命题不一定是真命题.
即学即练
例1 如图,在四边形ABCD中,AB=3,BC=4,
CD=12,AD=13,∠B=90°,求四边形ABCD的面积.
解:∵ AB=3,BC=4,∠B=90°,
∴ AC=5.又∵ CD=12,AD=13,
∴ AC2+CD2=52+122=169.
又∵ AD2=132=169,
即 AC2+CD2=AD2,
∴ △ACD是直角三角形.
∴ 四边形ABCD的面积为 .
A
B
C
D
合作探究
1、已知2条线段的长分别为3cm的长为_______cm时,这3条线段能组成一个直角三角形.
即学即练
2、A、B、C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
即学即练
3、小明向东走80米后,沿另一方向
又走了60米,再沿第三个方向走100
米回到原地.小明向东走80米后是向哪
个方向走的?
解:根据题意得: ∵802+602=1002
∴小明行走的轨迹,是直角三角形.
∴小明向东走80米后是向南或向北走的。
即学即练
4、一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图所示,你说这个零件符合要求吗?
即学即练
解:∵32+42=52,52+122=132;
即AD2+AB2=BD2,BD2+BC2=DC2;
∴∠A和∠DBC都是直角
∴这个零件符合要求.
即学即练
问题 通过例1及例2的学习,我们进一步学习了
像18,24,30;3,4,5;5,12,13这样的勾股数,大
家有没有发现18,24,30;3,4,5 这两组勾股数有什
么关系?
追问1 类似这样的关系6,8,10;9,12,15是否
也是勾股数?如何验证?
追问2 通过对以上勾股数的研究,你有什么样的
猜想?
即学即练
问题 通过例1及例2的学习,我们进一步学习了
像18,24,30;3,4,5;5,12,13这样的勾股数,大
家有没有发现18,24,30;3,4,5 这两组勾股数有什
么关系?
结论:若a,b,c是一组勾股数,那么ak,bk,ck
(k为正整数)也是一组勾股数.
拓展练习
1、勾股定理的逆定理是判定
______________________的一个依据.
一个三角形是不是直角三角形
2、互逆命题:两个命题的题设和结论正
好相反.像这样的叫做 _________.如果把
其中一个叫做原题,那么另一个叫做它的
__________.
互逆命题
逆命题
3、如果一个定理的逆命题经过证明是正
确的,那么它也是一个定理,我们称这
两个定理_________
互为逆命题
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
社会犹如一条船,每个人都要有掌舵的准备.
—— 易卜生
17.2 勾股定理逆定理
人教版八年级数学 下册
目标导航
1.探究勾股定理的逆定理及二者关系。
2.得出逆命题的概念,知道原命题为真命题,它的逆命题不一定为真命题。
3.应用勾股定理的逆定理解决实际问题。
目标导航一
勾股定理逆定理
勾股定理 如果直角三角形的两条直角边长分别为
a,b,斜边长为c,那么a2+b2=c2.
题设(条件):直角三角形的
两直角边长为a,b,斜边长为c .
结论:a2+b2=c2.
问题1 回忆勾股定理的内容.
形
数
复习回顾
思考 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是否是直角三角形?
逆向思考
据说,古埃及人曾用下面的方法画直角:把一根长
绳打上等距离的13 个结,然后以3 个结间距,4 个结间
距、5 个结间距的长度为边长,用木桩钉成一个三角形,
其中一个角便是直角.你认为结论正确吗?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
如果三角形的三边分别
为3,4,5,这些数满足
关系:32+42=52,围成的
三角形是直角三角形.
逆向思考
(1)画一画:下列各组数中的两数平方和等于第三数的 平方,分别以这些数为边长画出三角形(单位:cm), 它们是直角三角形吗?
① 2.5,6,6.5; ② 6,8,10.
(2)量一量:用量角器分别测量上述各三角形的最大角 的度数.
(3)想一想:请判断这些三角形的形状,并提出猜想.
实验操作
A1
B1
C1
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
?
三角形全等
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
a
证明结论
作用:判定一个三角形三边满足什么条件时为直角三角形.
定理:如果三角形的三边长a,b,c 满足a2+b2=c2,
那么这个三角形是直角三角形.
形成定理
知识点一 勾股定理的逆定理
画△ABC,使①a=3cm,b=4cm,c=5cm;
②a=2.5cm,b=6cm,c=6.5cm;
③a=4cm,b=7.5cm,c=8.5cm.
以上a、b、c的关系都满足__________;
△ABC是________ 三角形.
a2+b2=c2
直角
认真阅读课本第31至32页的内容,完成下面练习并体验知识点的形成过程.
自主研学
知识点一 勾股定理的逆定理
结论:命题2(勾股定理的逆定理)
如果三角形的三边长a、b、c,满足 ,
那么这个三角形是 三角形.
直角
自主研学
如果三条线段长a、b、c满足 ,这三条线段组成的三角形是不是直角三角形?为什么?
解:
根据题意,因为三角形的三边长度a、b、c满足a2+b2=c2 ,则根据勾股定理的逆定理,这个三角形是直角三角形.
即学即练
知识点二 证明勾股定理的逆定理
已知:△ABC的三边长分别为a、b、c,且a2+b2=c2. 求证:∠C=90°.
合作探究
知识点二 证明勾股定理的逆定理
证明:作Rt△A′B′C′,使∠C′= 90°,B′C′= BC = a, A′C′= AC = b.
∵A'B'2=B'C'2+A'C'2= ________=____
∴A'B' =_______
在△ABC和△A'B'C'中
________________________
________________________
________________________
AB=A'B'
AC=A'C'
BC=B'C'
∴_________≌________(SSS)
∴∠C=_______=90°.
BC2+AC2
AB2
AB
∠ C'
△ABC
△ A'B'C'
合作探究
知识点三 勾股定理的逆定理的运用
例1 判断由线段a、b、c组成的三角形是不是直角三角形:(1)a=15,b=8,c=17.
(2)a=13,b=14,c=15.
解:(1)因为152+82= __________= _____
172=_____
所以 + = ,
根据________________,这三角形是直角三角形.注:像8,15,17这样能够成为_____________ ________的三个__ ____,称为勾股数
225+64
289
289
152
82
172
勾股定理的逆定理
直角三角形三
条边长
正整数
合作探究
知识点三 勾股定理的逆定理的运用
例1 判断由线段a、b、c组成的三角形是不是直角三角形:(1)a=15,b=8,c=17.
(2)a=13,b=14,c=15.
(2)因为132+142= ___________= _____
152=_____
所以 + ≠ ,
根据_______ _______,这个三角形不是直角三角形.
169+16
185
225
132
42
152
勾股定理的逆定理
合作探究
1、下列四组数中:
①1、、2;②32,42,52 ;③9,40,41;④3k、4k、5k(k为正整数).
属于勾股数的有__________(填序号).
③④
即学即练
(1)a=7,b=24,c=25(2)a= ,b=4,c=5
(3)a= ,b=1,c= (4)a=40,b=50,c=60.
解:(1)因为a2+b2=49+576=625,
c2=252=625 a2+b2=c2
所以,根据勾股定理的逆定理,
a、b、c组成的三角形是直角三角形
即学即练
2、判断由线段a、b、c组成的三角形是不是直角三角形:
(2)因为b2+c2=16+25=41, a2=41
b2+c2=a2
所以,根据勾股定理的逆定理,a、b、c组成的三角形是直角三角形
解:(3)因为c2+b2=
a2= , c2+b2=a2
所以,根据勾股定理的逆定理,a、b、c组成的三角形是直角三角形
解:(4)因为a2+b2=1600+2500=4100, c2=3600 , a2+b2≠c2
所以,根据勾股定理的逆定理,a、b、c组成的三角形不是直角三角形
勾股定理的逆定理:
定理:如果三角形的三边长a,b,c 满足a2+b2=c2,
那么这个三角形是直角三角形.
勾股定理:如果直角三角形两直角边分别为a,b,
斜边为c,那么a2+b2=c2.
归纳小结
正整数
能够成为直角三角形三条边长的三个____________,称为勾股数.
目标导航二
勾股定理逆定理的应用
1、命题1(勾股定理) 如果直角三角形的两
条直角边长分别为a,b,斜边长为c,那么
__________.
a2+b2=c2
2、命题2(勾股定理的逆定理)
如果三角形的三边长a、b、c,满足
那么这个三角形是 ___________ 三角形.
a2+b2=c2
直角
理论梳理
认真阅读课本第31至33页的内容,完成下面练习并体验知识点的形成过程.
原命题、逆命题和逆定理
自主研学
1、上面命题1与命题2的题设和结论正好______.像这样的两个命题叫做_____,命题;如果把其中一个叫做原命题,那么另一个叫做它的__________.
相反
互逆
逆命题
2、一般地,原命题成立时,它的逆命题
既可能成立,也可能不成立.如果一个定理
的逆命题经过证明是_______________,
那么它也是一个定理,我们称这两个定理
互为逆定理.
正确的
合作探究
定理与逆定理
我们已经学习过哪些互逆的定理?
(1)任何一个命题都有逆命题;
原命题与逆命题的关系是题设和结论相互转换
(2)原命题正确,逆命题不一定正确;原命题不正确,逆命题可能正确。
(3)一个定理未必有逆定理。
(1)等腰三角形的两底角相等
原命题:如果一个三角形是等腰三角形,那么这个三角形的两底角相等。
逆命题:如果一个三角形的两底角相等,那么这个三角形是等腰三角形。
写出下列命题的逆命题并判断它们是否成立:
(2)两直线平行,同位角相等
原命题:如果两条直线平行,那么同位角相等。
逆命题:如果同位角相等,那么两直线平行。
(3)三内角之比为1:2:3的三角形为
直角三角形
原命题:如果一个三角形三内角之比为1:2:3,
那么这个三角形是直角三角形。
逆命题:如果一个三角形是直角三角形,
那么这个三角形三内角之比为1:2:3。
1、说出下列命题的逆命题.这些逆命题
成立吗?
⑶全等三角形的对应角相等;
⑷在角的内部,到角的两边距离相等的点
在角的平分线上.
答:逆命题为:对应角相等的三角形全等 。
不成立
答:逆命题为:在角平分线上的点到角的两
边距离相等。 成立
即学即练
说出下列命题的逆命题.这些命题的逆命题是真命
题吗?
(1)两条直线平行,内错角相等;
逆命题:内错角相等,两直线平行.真命题.
(2)对顶角相等;
逆命题:相等的角是对顶角.假命题.
(3)线段垂直平分线上的点到线段两端点的距离相等.
逆命题:到线段两端点的距离相等的点在线段的
垂直平分线上.真命题.
任何一个命题都有逆
命题;原命题是真命题,其
逆命题不一定是真命题.
即学即练
例1 如图,在四边形ABCD中,AB=3,BC=4,
CD=12,AD=13,∠B=90°,求四边形ABCD的面积.
解:∵ AB=3,BC=4,∠B=90°,
∴ AC=5.又∵ CD=12,AD=13,
∴ AC2+CD2=52+122=169.
又∵ AD2=132=169,
即 AC2+CD2=AD2,
∴ △ACD是直角三角形.
∴ 四边形ABCD的面积为 .
A
B
C
D
合作探究
1、已知2条线段的长分别为3cm的长为_______cm时,这3条线段能组成一个直角三角形.
即学即练
2、A、B、C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
即学即练
3、小明向东走80米后,沿另一方向
又走了60米,再沿第三个方向走100
米回到原地.小明向东走80米后是向哪
个方向走的?
解:根据题意得: ∵802+602=1002
∴小明行走的轨迹,是直角三角形.
∴小明向东走80米后是向南或向北走的。
即学即练
4、一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图所示,你说这个零件符合要求吗?
即学即练
解:∵32+42=52,52+122=132;
即AD2+AB2=BD2,BD2+BC2=DC2;
∴∠A和∠DBC都是直角
∴这个零件符合要求.
即学即练
问题 通过例1及例2的学习,我们进一步学习了
像18,24,30;3,4,5;5,12,13这样的勾股数,大
家有没有发现18,24,30;3,4,5 这两组勾股数有什
么关系?
追问1 类似这样的关系6,8,10;9,12,15是否
也是勾股数?如何验证?
追问2 通过对以上勾股数的研究,你有什么样的
猜想?
即学即练
问题 通过例1及例2的学习,我们进一步学习了
像18,24,30;3,4,5;5,12,13这样的勾股数,大
家有没有发现18,24,30;3,4,5 这两组勾股数有什
么关系?
结论:若a,b,c是一组勾股数,那么ak,bk,ck
(k为正整数)也是一组勾股数.
拓展练习
1、勾股定理的逆定理是判定
______________________的一个依据.
一个三角形是不是直角三角形
2、互逆命题:两个命题的题设和结论正
好相反.像这样的叫做 _________.如果把
其中一个叫做原题,那么另一个叫做它的
__________.
互逆命题
逆命题
3、如果一个定理的逆命题经过证明是正
确的,那么它也是一个定理,我们称这
两个定理_________
互为逆命题
归纳小结
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
