人教版小学五年级数学(下)第5章 图形的运动(三) 单元测试题(有答案)
文档属性
| 名称 | 人教版小学五年级数学(下)第5章 图形的运动(三) 单元测试题(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 00:00:00 | ||
图片预览



文档简介
人教版小学五年级数学(下)第5章 图形的运动(三) 单元测试题
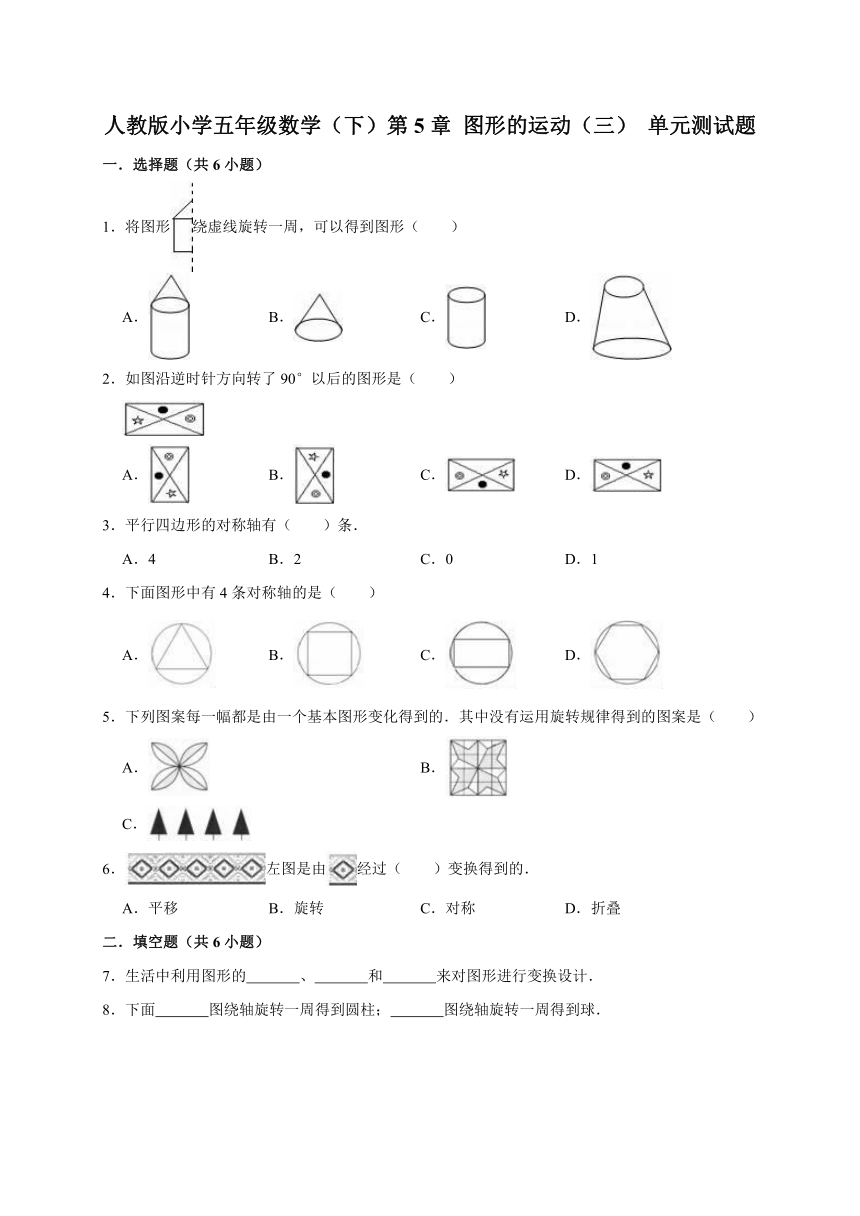
一.选择题(共6小题)
1.将图形绕虚线旋转一周,可以得到图形( )
A. B. C. D.
2.如图沿逆时针方向转了90°以后的图形是( )
A. B. C. D.
3.平行四边形的对称轴有( )条.
A.4 B.2 C.0 D.1
4.下面图形中有4条对称轴的是( )
A. B. C. D.
5.下列图案每一幅都是由一个基本图形变化得到的.其中没有运用旋转规律得到的图案是( )
A. B.
C.
6.左图是由经过( )变换得到的.
A.平移 B.旋转 C.对称 D.折叠
二.填空题(共6小题)
7.生活中利用图形的 、 和 来对图形进行变换设计.
8.下面 图绕轴旋转一周得到圆柱; 图绕轴旋转一周得到球.
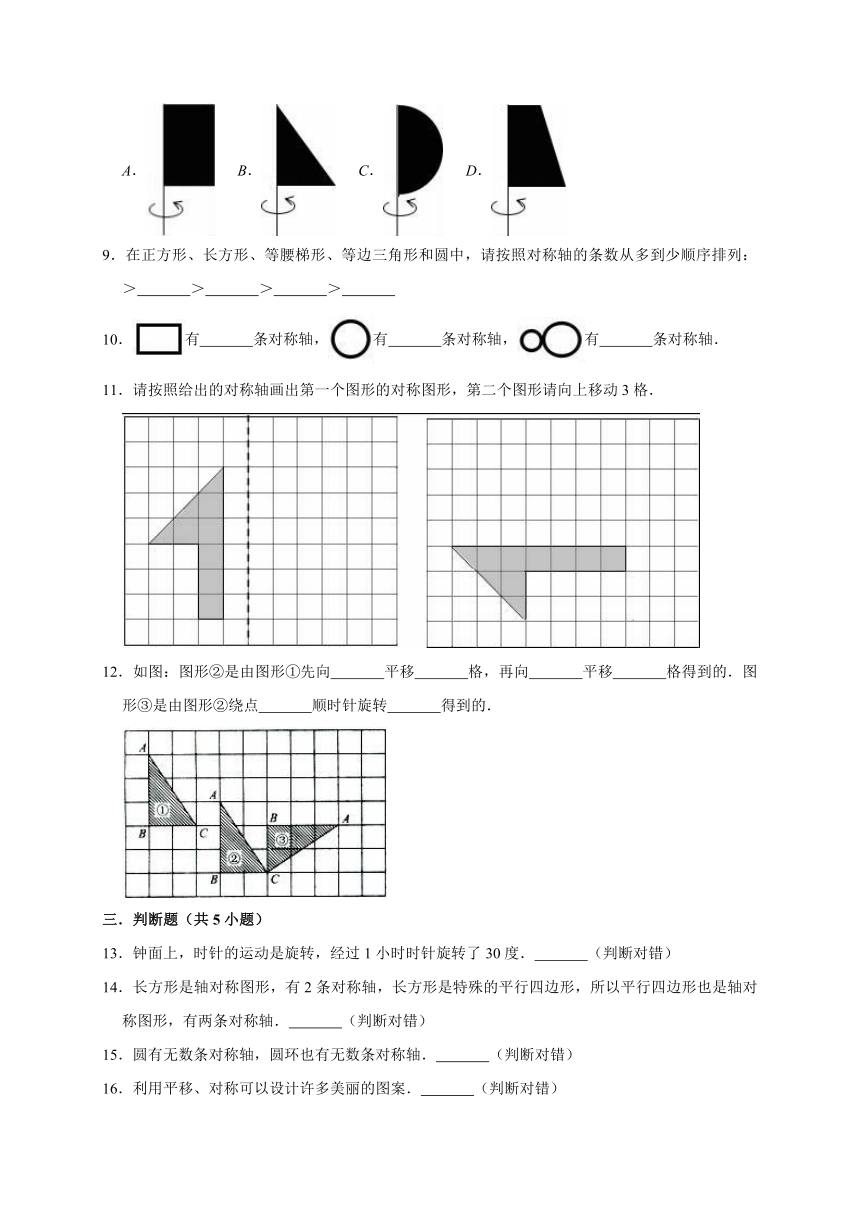
A. B. C. D.
9.在正方形、长方形、等腰梯形、等边三角形和圆中,请按照对称轴的条数从多到少顺序排列: > > > >
10.有 条对称轴,有 条对称轴,有 条对称轴.
11.请按照给出的对称轴画出第一个图形的对称图形,第二个图形请向上移动3格.
12.如图:图形②是由图形①先向 平移 格,再向 平移 格得到的.图形③是由图形②绕点 顺时针旋转 得到的.
三.判断题(共5小题)
13.钟面上,时针的运动是旋转,经过1小时时针旋转了30度. (判断对错)
14.长方形是轴对称图形,有2条对称轴,长方形是特殊的平行四边形,所以平行四边形也是轴对称图形,有两条对称轴. (判断对错)
15.圆有无数条对称轴,圆环也有无数条对称轴. (判断对错)
16.利用平移、对称可以设计许多美丽的图案. (判断对错)
17.如图,将等边三角形图形绕着点O旋转120°后与原来图形重合. (判断对错)
四.操作题(共2小题)
18.请你在下面的方格纸上设计出面积为10平方厘米的图案,你能画出几种?(至少设计出2种图案,每个□
代表1平方厘米)
19.如图哪些图形是对称图形?是的请在□里画“√”.
五.解答题(共3小题)
20.一个正三角形绕其一顶点按同一方向连续旋转五次,每次转过的角数为60°,旋转前后所有的图形共同组成的图案是什么?请你在方格纸中画出来.
21.画出下面各图的一条对称轴.
22.请你用轴对称或平移的方法,设计一幅美丽的图案.
参考答案与试题解析
一.选择题(共6小题)
1.解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,
所以旋转得出的图形上部是一个圆锥体,下部是一个圆柱体.
故选:A.
2.解根据旋转的定义可得,将翻转后的图形按逆时针方向旋转90°得到的图形是:
故选:A.
3.解:根据轴对称图形的意义可知:平行四边形不是轴对称图形,没有对称轴.
故选:C.
4.解:A,有3条对称轴;
B,有4条对称轴;
C,有2条对称轴;
D,有6条对称轴,
故选:B.
5.解:图形1可由一个基本“花瓣”绕其中心经过4次旋转,每次旋转90°得到;
图形2可由一个基本“不规则5边形”绕其中心经过4次旋转,每次旋转90°得到;
图形3可由一个基本图形三角形经过平移得到;
其中没有运用旋转规律得到的图案是C;
故选:C.
6.解:采用平移的方法,平移4次,复制下图案,即可得到左图.
故选:A.
二.填空题(共6小题)
7.解:生活中利用图形的平移、旋转和轴对称来对图形进行变换设计.
故答案为:平移、旋转、轴对称.
8.解:根据题干分析可得,圆柱是由一个长方形绕着一条边旋转得到的,球体是由一个半圆绕直径旋转一周得到的;
故选:A;C.
9.解:据轴对称图形的特点和定义可知:正方形由四条对称轴,长方形有两条对称轴,等边三角形有三条对称轴,圆形有无数条对称轴,等腰梯形有一条对称轴;
答:这几种图形按对称轴的多少排列是这样的:圆形>正方形>等边三角形>长方形>等腰梯形.
故答案为:圆形、正方形、等边三角形、长方形、等腰梯形.
10.解:有2条对称轴,有无数条对称轴,有1条对称轴.
故答案为:2,无数,1.
11.解:作图如下:
12.解:如图,
图形②是由图形①先向右(下)平移3(或2)格,再向下(右)平移2(或3)格得到的.图形③是由图形②绕点点C顺时针旋转90°得到的.
故答案为:右(下),3(或2),下(右),2(或3),点C,90°.
三.判断题(共5小题)
13.解:因为时钟上的时针匀速旋转一周的度数为360°,时钟上的时针匀速旋转一周需要12小时,
则时钟上的时针匀速旋转一小时的度数为:360÷12=30(度),
故答案为:√.
14.解:长方形是轴对称图形,有2条对称轴,长方形是特殊的平行四边形,这些说法都是正确的;
但一般的平行四边形不是轴对称图形,所以原题说法错误.
故答案为:×.
15.解:根据轴对称图形的意义可知:圆有无数条对称轴,圆环也有无数条对称轴,所以说法正确;
故答案为:√.
16.解:根据分析画图如下:
故答案为:√.
17.解:360°÷3=120°,
该图形绕中心至少旋转120度后能和原来的图案互相重合,所以本题说法正确;
故答案为:√.
四.操作题(共2小题)
18.解:
19.解:根据轴对称图形的意义可知:
五.解答题(共3小题)
20.解:因为当一个正三角形绕其顶点按同一方向连续旋转5次,每次转过的角度都是60°时,其中心角恰为360°,组成的图形每个角为120°,
所以此多边形为正六边形.
画图如下:
21.解:
22.解:用轴对称或平移的方法,设计一幅美丽的图案:
一.选择题(共6小题)
1.将图形绕虚线旋转一周,可以得到图形( )
A. B. C. D.
2.如图沿逆时针方向转了90°以后的图形是( )
A. B. C. D.
3.平行四边形的对称轴有( )条.
A.4 B.2 C.0 D.1
4.下面图形中有4条对称轴的是( )
A. B. C. D.
5.下列图案每一幅都是由一个基本图形变化得到的.其中没有运用旋转规律得到的图案是( )
A. B.
C.
6.左图是由经过( )变换得到的.
A.平移 B.旋转 C.对称 D.折叠
二.填空题(共6小题)
7.生活中利用图形的 、 和 来对图形进行变换设计.
8.下面 图绕轴旋转一周得到圆柱; 图绕轴旋转一周得到球.
A. B. C. D.
9.在正方形、长方形、等腰梯形、等边三角形和圆中,请按照对称轴的条数从多到少顺序排列: > > > >
10.有 条对称轴,有 条对称轴,有 条对称轴.
11.请按照给出的对称轴画出第一个图形的对称图形,第二个图形请向上移动3格.
12.如图:图形②是由图形①先向 平移 格,再向 平移 格得到的.图形③是由图形②绕点 顺时针旋转 得到的.
三.判断题(共5小题)
13.钟面上,时针的运动是旋转,经过1小时时针旋转了30度. (判断对错)
14.长方形是轴对称图形,有2条对称轴,长方形是特殊的平行四边形,所以平行四边形也是轴对称图形,有两条对称轴. (判断对错)
15.圆有无数条对称轴,圆环也有无数条对称轴. (判断对错)
16.利用平移、对称可以设计许多美丽的图案. (判断对错)
17.如图,将等边三角形图形绕着点O旋转120°后与原来图形重合. (判断对错)
四.操作题(共2小题)
18.请你在下面的方格纸上设计出面积为10平方厘米的图案,你能画出几种?(至少设计出2种图案,每个□
代表1平方厘米)
19.如图哪些图形是对称图形?是的请在□里画“√”.
五.解答题(共3小题)
20.一个正三角形绕其一顶点按同一方向连续旋转五次,每次转过的角数为60°,旋转前后所有的图形共同组成的图案是什么?请你在方格纸中画出来.
21.画出下面各图的一条对称轴.
22.请你用轴对称或平移的方法,设计一幅美丽的图案.
参考答案与试题解析
一.选择题(共6小题)
1.解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,
所以旋转得出的图形上部是一个圆锥体,下部是一个圆柱体.
故选:A.
2.解根据旋转的定义可得,将翻转后的图形按逆时针方向旋转90°得到的图形是:
故选:A.
3.解:根据轴对称图形的意义可知:平行四边形不是轴对称图形,没有对称轴.
故选:C.
4.解:A,有3条对称轴;
B,有4条对称轴;
C,有2条对称轴;
D,有6条对称轴,
故选:B.
5.解:图形1可由一个基本“花瓣”绕其中心经过4次旋转,每次旋转90°得到;
图形2可由一个基本“不规则5边形”绕其中心经过4次旋转,每次旋转90°得到;
图形3可由一个基本图形三角形经过平移得到;
其中没有运用旋转规律得到的图案是C;
故选:C.
6.解:采用平移的方法,平移4次,复制下图案,即可得到左图.
故选:A.
二.填空题(共6小题)
7.解:生活中利用图形的平移、旋转和轴对称来对图形进行变换设计.
故答案为:平移、旋转、轴对称.
8.解:根据题干分析可得,圆柱是由一个长方形绕着一条边旋转得到的,球体是由一个半圆绕直径旋转一周得到的;
故选:A;C.
9.解:据轴对称图形的特点和定义可知:正方形由四条对称轴,长方形有两条对称轴,等边三角形有三条对称轴,圆形有无数条对称轴,等腰梯形有一条对称轴;
答:这几种图形按对称轴的多少排列是这样的:圆形>正方形>等边三角形>长方形>等腰梯形.
故答案为:圆形、正方形、等边三角形、长方形、等腰梯形.
10.解:有2条对称轴,有无数条对称轴,有1条对称轴.
故答案为:2,无数,1.
11.解:作图如下:
12.解:如图,
图形②是由图形①先向右(下)平移3(或2)格,再向下(右)平移2(或3)格得到的.图形③是由图形②绕点点C顺时针旋转90°得到的.
故答案为:右(下),3(或2),下(右),2(或3),点C,90°.
三.判断题(共5小题)
13.解:因为时钟上的时针匀速旋转一周的度数为360°,时钟上的时针匀速旋转一周需要12小时,
则时钟上的时针匀速旋转一小时的度数为:360÷12=30(度),
故答案为:√.
14.解:长方形是轴对称图形,有2条对称轴,长方形是特殊的平行四边形,这些说法都是正确的;
但一般的平行四边形不是轴对称图形,所以原题说法错误.
故答案为:×.
15.解:根据轴对称图形的意义可知:圆有无数条对称轴,圆环也有无数条对称轴,所以说法正确;
故答案为:√.
16.解:根据分析画图如下:
故答案为:√.
17.解:360°÷3=120°,
该图形绕中心至少旋转120度后能和原来的图案互相重合,所以本题说法正确;
故答案为:√.
四.操作题(共2小题)
18.解:
19.解:根据轴对称图形的意义可知:
五.解答题(共3小题)
20.解:因为当一个正三角形绕其顶点按同一方向连续旋转5次,每次转过的角度都是60°时,其中心角恰为360°,组成的图形每个角为120°,
所以此多边形为正六边形.
画图如下:
21.解:
22.解:用轴对称或平移的方法,设计一幅美丽的图案:
