五年级下册数学课件-第7单元 第1课时 解决问题的策略——转化 苏教版(共29张PPT)
文档属性
| 名称 | 五年级下册数学课件-第7单元 第1课时 解决问题的策略——转化 苏教版(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览



文档简介
(共29张PPT)
用转化的策略解决
问题(1)
司马光砸缸
人离开水
转化
水离开人
导入新课
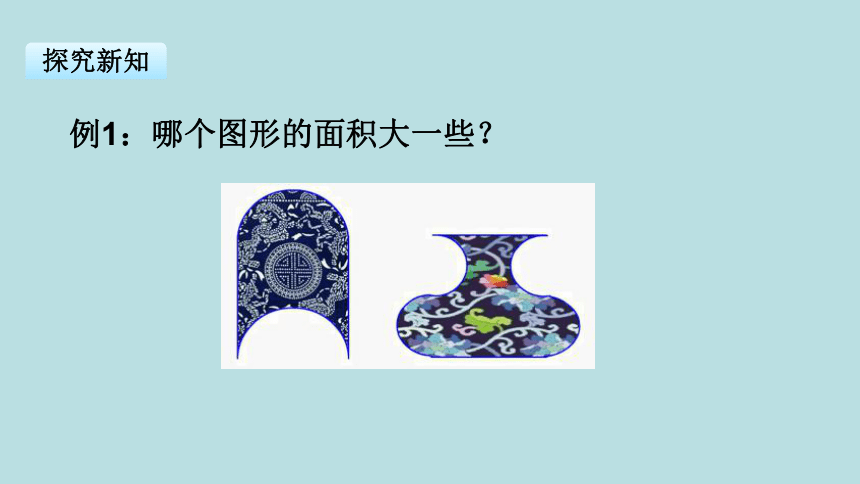
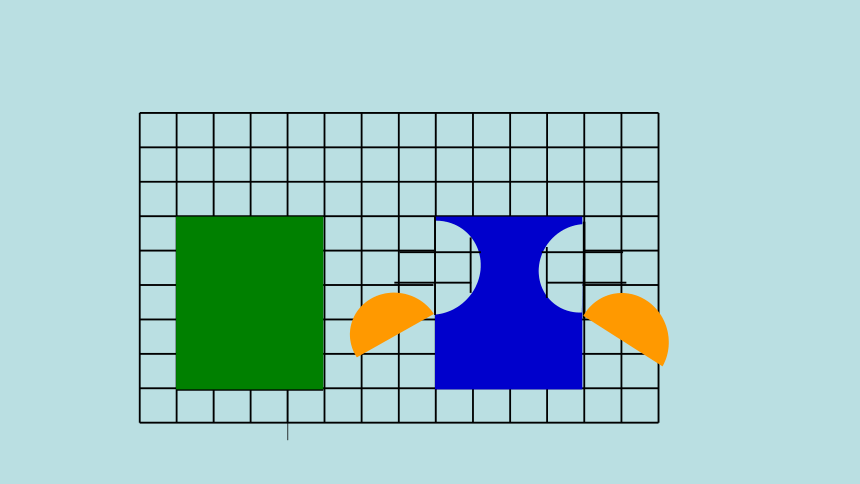
例1:哪个图形的面积大一些?
探究新知
探究新知
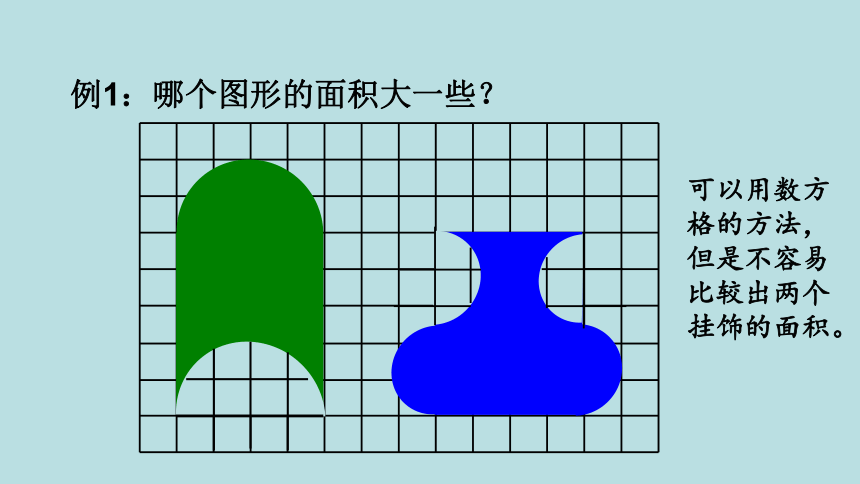
例1:哪个图形的面积大一些?
可以用数方格的方法,但是不容易比较出两个挂饰的面积。
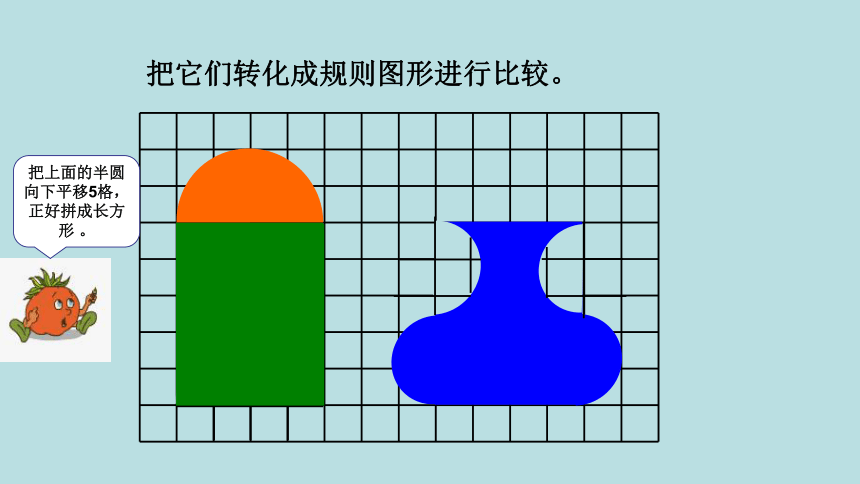
把它们转化成规则图形进行比较。
把上面的半圆向下平移5格,正好拼成长方形 。
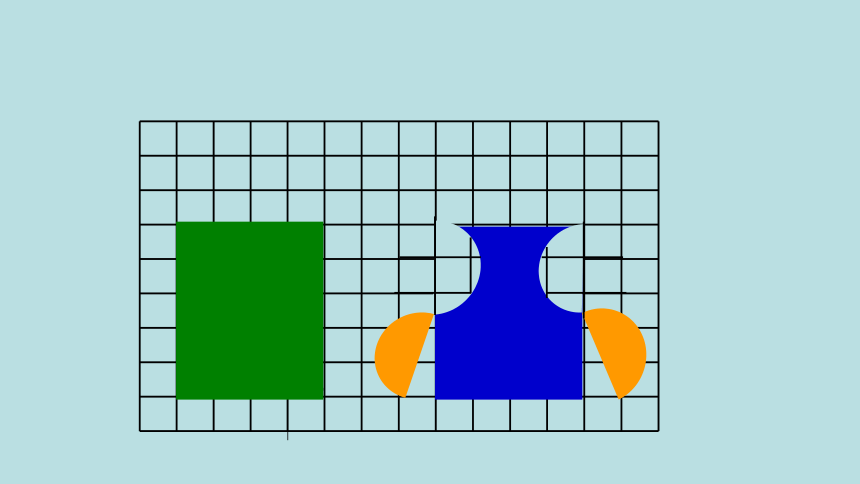
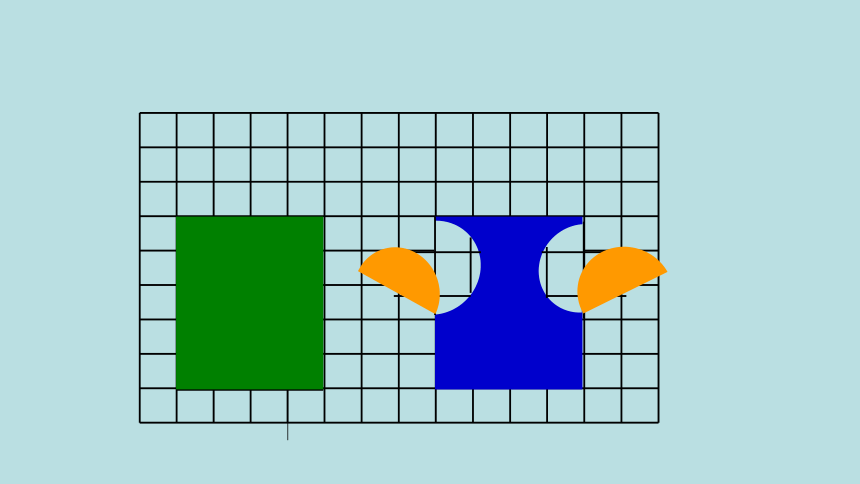
把它们转化成规则图形进行比较。
把2个半圆分别旋转180°,也拼成长方形。
因为两个长方形面积相等,所以原来两个图形面积相等。
复杂
简单
转化
回顾解决问题的过程,你有什么体会?
有些不规则的图形可以转化成熟悉的简单的图形。
图形转化时可以运用平移、旋转等方法。
转化后的图形与转化前相比,形状变了,大小没有变。
a
h
a
h
图形中的转化
回顾反思
我们在以前的学习中曾运用转化的策略解决过哪些问题?
a
h
h
a
a
图形中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
a
h
b
a
h
a
b
b
图形中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
图形中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
新知
旧知
转化
a
a
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
小数乘法
整数乘法
3.25×1.3
325×13
计算中的转化
我们在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
除数是小数的除法
除数是整数的除法
4.76÷ 2.4
47.6÷ 24
计算中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
异分母分数加减法
同分母分数加减法
+
2
1
3
1
+
6
3
6
2
计算中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
小 数 乘 法
整 数 乘 法
除数是小数的除法
除数是整数的除法
异分母分数加减法
同分母分数加减法
新知
旧知
转化
在以前的学习中曾运用转化的策略解决过哪些问题?
(5+3) ×2=16(厘米)
1.每个小方格的边长是1厘米,下面两个图形的周长相等吗?
巩固练习
1m
1×4=4(m)
r=4 cm
0
2.计算下面图形的周长。
大圆周长的一半:4×2×3.14÷2=12.56(cm)
小圆的周长:3.14×4=12.56(cm)
12.56+12.56=25.12(cm)
r=4 cm
0
3.用分数表示各图中的涂色部分。
(1)
(4)
(1)
(2)
(12)
(16)
拓展练习
4.
课堂总结
新知转化为旧知
复杂转化为简单
解决问题的策略
——转化
数学阅读
一天,爱迪生要他的助手帮忙测量一个灯泡的容积,这个助手不简单,他是爱迪生在大学里千挑万选的,助手拿着这只梨形的灯泡,看了量,量了看,还画出了各种示意图,列出了一道道算式。一个钟头过去了,他才算了一半。
爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是灯泡的容积。”助手恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。
用转化的策略解决
问题(1)
司马光砸缸
人离开水
转化
水离开人
导入新课
例1:哪个图形的面积大一些?
探究新知
探究新知
例1:哪个图形的面积大一些?
可以用数方格的方法,但是不容易比较出两个挂饰的面积。
把它们转化成规则图形进行比较。
把上面的半圆向下平移5格,正好拼成长方形 。
把它们转化成规则图形进行比较。
把2个半圆分别旋转180°,也拼成长方形。
因为两个长方形面积相等,所以原来两个图形面积相等。
复杂
简单
转化
回顾解决问题的过程,你有什么体会?
有些不规则的图形可以转化成熟悉的简单的图形。
图形转化时可以运用平移、旋转等方法。
转化后的图形与转化前相比,形状变了,大小没有变。
a
h
a
h
图形中的转化
回顾反思
我们在以前的学习中曾运用转化的策略解决过哪些问题?
a
h
h
a
a
图形中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
a
h
b
a
h
a
b
b
图形中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
图形中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
新知
旧知
转化
a
a
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
小数乘法
整数乘法
3.25×1.3
325×13
计算中的转化
我们在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
除数是小数的除法
除数是整数的除法
4.76÷ 2.4
47.6÷ 24
计算中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
异分母分数加减法
同分母分数加减法
+
2
1
3
1
+
6
3
6
2
计算中的转化
在以前的学习中曾运用转化的策略解决过哪些问题?
回顾反思
小 数 乘 法
整 数 乘 法
除数是小数的除法
除数是整数的除法
异分母分数加减法
同分母分数加减法
新知
旧知
转化
在以前的学习中曾运用转化的策略解决过哪些问题?
(5+3) ×2=16(厘米)
1.每个小方格的边长是1厘米,下面两个图形的周长相等吗?
巩固练习
1m
1×4=4(m)
r=4 cm
0
2.计算下面图形的周长。
大圆周长的一半:4×2×3.14÷2=12.56(cm)
小圆的周长:3.14×4=12.56(cm)
12.56+12.56=25.12(cm)
r=4 cm
0
3.用分数表示各图中的涂色部分。
(1)
(4)
(1)
(2)
(12)
(16)
拓展练习
4.
课堂总结
新知转化为旧知
复杂转化为简单
解决问题的策略
——转化
数学阅读
一天,爱迪生要他的助手帮忙测量一个灯泡的容积,这个助手不简单,他是爱迪生在大学里千挑万选的,助手拿着这只梨形的灯泡,看了量,量了看,还画出了各种示意图,列出了一道道算式。一个钟头过去了,他才算了一半。
爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是灯泡的容积。”助手恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。
