教新课标A版选修4-4第一章 坐标系 1.1.1平面直角坐标系(共26张PPT)
文档属性
| 名称 | 教新课标A版选修4-4第一章 坐标系 1.1.1平面直角坐标系(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 869.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 21:51:12 | ||
图片预览








文档简介
(共26张PPT)
1.1.1平面直角坐标系的建立
1.1.2平面直角坐标系中的伸缩变换
新课导入
仔细观察发电厂冷却塔的外部形状,如何在平面直角坐标系中建立合理的坐标系来表示该形状呢?
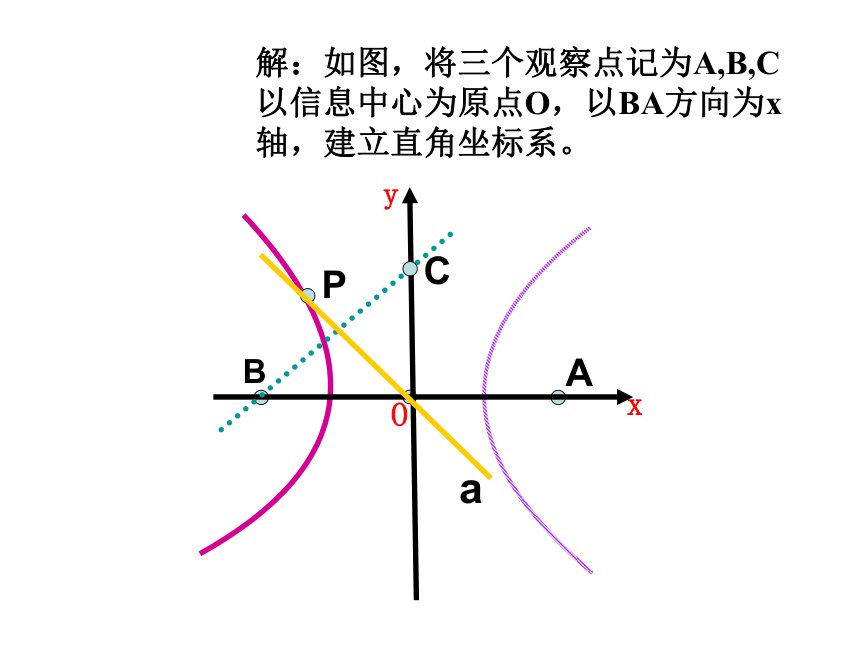
某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1024m,试确定该巨响的位置。 (假定当时声音传播的速度为340m/s,各相关点均在同一面上)
解:如图,将三个观察点记为A,B,C以信息中心为原点O,以BA方向为x轴,建立直角坐标系。
y
x
A
C
P
B
O
a
由题意得A,B,C的坐标分别为A(1020,0) B(-1020,0) C(0,1020)。
由于B,C同时听到点P发出的声音,因此|PB|=|PC|,说明点P在线段BC的垂直平分线上;由于A比B晚4S听到响声,故|PA|-|PB|=4×340=1360<|AB|,说明点P在以点A,B为焦点的双曲线上.所以点P就是直线a和双曲线的交点。
a
由题意得直线a的方程为:
设双曲线方程为:
又
用y=-x代入上式,得
由已知,|PA|>|PB|
因此响声在信息中心的西偏北45°方向,距离 处
解决此类应用题的关键:
1.建立平面直角坐标系
2.设点(点与坐标的对应)
3.列式(方程与坐标的对应)
4.化简
5.说明
坐 标 法
(1)怎样由正弦曲线
得到曲线 ?
(2)怎样由正弦曲线
得到曲线 ?
(3)怎样由正弦曲线
得到曲线 ?
x
O
?
2?
y=sin2x
(1)
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原的 ,就得到正弦曲线y=sin2x。
y=sinx
y
保持纵坐标y不变,将横坐标缩为原来的 的实质是什么?
新课导入
实际上这是一个坐标的压缩变换,即:
设P(x,y)是平面直角坐标系中任意一
点,保持纵坐标y不变,将横坐标x缩为原
来 ,得到点 坐标对应关
系为:
(1)
我们把(1)式叫做平面直角坐标系中的一个压缩变换。
(2)同理,在正弦曲线上任取一点P(x,y),保持横坐标x不变将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。
设点P变换后的点
则
(2)
我们把(2)式叫做平面直角坐标系中的一个伸长变换。
(3)同理,在正弦曲线上任取一点P(x,y),保持纵坐标y不变横坐标x缩为原来的 ;在此基础上再将纵坐标y变为原来的3倍,就得到曲线y=3sin2x。
设点P变换后的点
则
(3)
我们把(3)式叫做平面直角坐标系中的一个伸缩变换。
定义:设P(x,y)是平面直角坐标
系中任意一点,在变换
的作用下,点P(x,y)对应
称 为
平面直角坐标系中的坐标伸缩变换。
1.在同一平面直角坐标系中,求下列方程
所对应的图形经过伸缩变换
后的图形
(1)
(2)
解:由伸缩变换 得
将此式代入 ,
得到方程 ,因此经过伸缩变化
后,曲线
变成
体会坐标法思想,应用坐标法解决几何问题;
a.若图形有对称中心,可选对称中心为坐标原点;
b.若图形有对称轴,可以选对称轴为坐标轴;
c.图形上的特殊点尽可能多的在坐标轴上。
(2)掌握平面直角坐标系中的伸缩变换。
(1) 由正弦曲线 得到曲线
的过程,即 “在正弦曲线 上任
一点,保持纵坐标不变,横坐标缩为原来的 ”
(2)由正弦曲线 得到曲线
的过程,即“在正弦曲线
上任一点,保持横坐标不变,纵坐标伸长为原来的A倍”
由正弦曲线 得到曲线
的过程,即“在正弦曲线
上任一点保持纵坐标不变,
横坐标缩为原来的 ,再将纵坐标伸长
为原来的 倍”
(3)
1.求椭圆 上的点P到直线
的最大距离及此时P点坐标。
解:∵椭圆上的点
到直线的距离
当
(2018宁夏卷)已知曲线C1
( 为参数),曲线C2
( 为参数)
(1)指出C1,C2各为什么曲线,
并说明C1与C2公共点 的个数;
(2)若把C1,C2上各个点的纵坐标都
压缩为原来的一半,
分别得到曲线
写出 的参数方程。 与
公共点的个数和C1与C2公共点的个数
是否相同?说明你的理由.
解:(1)C1是圆,C2是直线
C1的普通方程为 圆心(0,0),
C2的普通方程为 ,
因为圆心C1到直线 的距离为1,
所以C1与C2只有一个公共点;
(2)压缩后的参数方程分别为( 和 均为参数)
化为普通方程为
联立消元得,
其判别式
所以压缩后的直线 与椭圆 仍然
只有一个公共点;和 与 公共点个数相同。
1.1.1平面直角坐标系的建立
1.1.2平面直角坐标系中的伸缩变换
新课导入
仔细观察发电厂冷却塔的外部形状,如何在平面直角坐标系中建立合理的坐标系来表示该形状呢?
某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1024m,试确定该巨响的位置。 (假定当时声音传播的速度为340m/s,各相关点均在同一面上)
解:如图,将三个观察点记为A,B,C以信息中心为原点O,以BA方向为x轴,建立直角坐标系。
y
x
A
C
P
B
O
a
由题意得A,B,C的坐标分别为A(1020,0) B(-1020,0) C(0,1020)。
由于B,C同时听到点P发出的声音,因此|PB|=|PC|,说明点P在线段BC的垂直平分线上;由于A比B晚4S听到响声,故|PA|-|PB|=4×340=1360<|AB|,说明点P在以点A,B为焦点的双曲线上.所以点P就是直线a和双曲线的交点。
a
由题意得直线a的方程为:
设双曲线方程为:
又
用y=-x代入上式,得
由已知,|PA|>|PB|
因此响声在信息中心的西偏北45°方向,距离 处
解决此类应用题的关键:
1.建立平面直角坐标系
2.设点(点与坐标的对应)
3.列式(方程与坐标的对应)
4.化简
5.说明
坐 标 法
(1)怎样由正弦曲线
得到曲线 ?
(2)怎样由正弦曲线
得到曲线 ?
(3)怎样由正弦曲线
得到曲线 ?
x
O
?
2?
y=sin2x
(1)
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原的 ,就得到正弦曲线y=sin2x。
y=sinx
y
保持纵坐标y不变,将横坐标缩为原来的 的实质是什么?
新课导入
实际上这是一个坐标的压缩变换,即:
设P(x,y)是平面直角坐标系中任意一
点,保持纵坐标y不变,将横坐标x缩为原
来 ,得到点 坐标对应关
系为:
(1)
我们把(1)式叫做平面直角坐标系中的一个压缩变换。
(2)同理,在正弦曲线上任取一点P(x,y),保持横坐标x不变将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。
设点P变换后的点
则
(2)
我们把(2)式叫做平面直角坐标系中的一个伸长变换。
(3)同理,在正弦曲线上任取一点P(x,y),保持纵坐标y不变横坐标x缩为原来的 ;在此基础上再将纵坐标y变为原来的3倍,就得到曲线y=3sin2x。
设点P变换后的点
则
(3)
我们把(3)式叫做平面直角坐标系中的一个伸缩变换。
定义:设P(x,y)是平面直角坐标
系中任意一点,在变换
的作用下,点P(x,y)对应
称 为
平面直角坐标系中的坐标伸缩变换。
1.在同一平面直角坐标系中,求下列方程
所对应的图形经过伸缩变换
后的图形
(1)
(2)
解:由伸缩变换 得
将此式代入 ,
得到方程 ,因此经过伸缩变化
后,曲线
变成
体会坐标法思想,应用坐标法解决几何问题;
a.若图形有对称中心,可选对称中心为坐标原点;
b.若图形有对称轴,可以选对称轴为坐标轴;
c.图形上的特殊点尽可能多的在坐标轴上。
(2)掌握平面直角坐标系中的伸缩变换。
(1) 由正弦曲线 得到曲线
的过程,即 “在正弦曲线 上任
一点,保持纵坐标不变,横坐标缩为原来的 ”
(2)由正弦曲线 得到曲线
的过程,即“在正弦曲线
上任一点,保持横坐标不变,纵坐标伸长为原来的A倍”
由正弦曲线 得到曲线
的过程,即“在正弦曲线
上任一点保持纵坐标不变,
横坐标缩为原来的 ,再将纵坐标伸长
为原来的 倍”
(3)
1.求椭圆 上的点P到直线
的最大距离及此时P点坐标。
解:∵椭圆上的点
到直线的距离
当
(2018宁夏卷)已知曲线C1
( 为参数),曲线C2
( 为参数)
(1)指出C1,C2各为什么曲线,
并说明C1与C2公共点 的个数;
(2)若把C1,C2上各个点的纵坐标都
压缩为原来的一半,
分别得到曲线
写出 的参数方程。 与
公共点的个数和C1与C2公共点的个数
是否相同?说明你的理由.
解:(1)C1是圆,C2是直线
C1的普通方程为 圆心(0,0),
C2的普通方程为 ,
因为圆心C1到直线 的距离为1,
所以C1与C2只有一个公共点;
(2)压缩后的参数方程分别为( 和 均为参数)
化为普通方程为
联立消元得,
其判别式
所以压缩后的直线 与椭圆 仍然
只有一个公共点;和 与 公共点个数相同。
