人教新课标A版选修4-4第一章 坐标系 1.3.1简单曲线的极坐标方程(共30张PPT)
文档属性
| 名称 | 人教新课标A版选修4-4第一章 坐标系 1.3.1简单曲线的极坐标方程(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 21:53:22 | ||
图片预览










文档简介
(共30张PPT)
1.3.1圆的极坐标方程
1.3.2直线的极坐标方程
在直角坐标系中,平面曲线C可以用
方程 表示,类似的,在极坐
标系中,是否也可以用方程表示?
新课导入
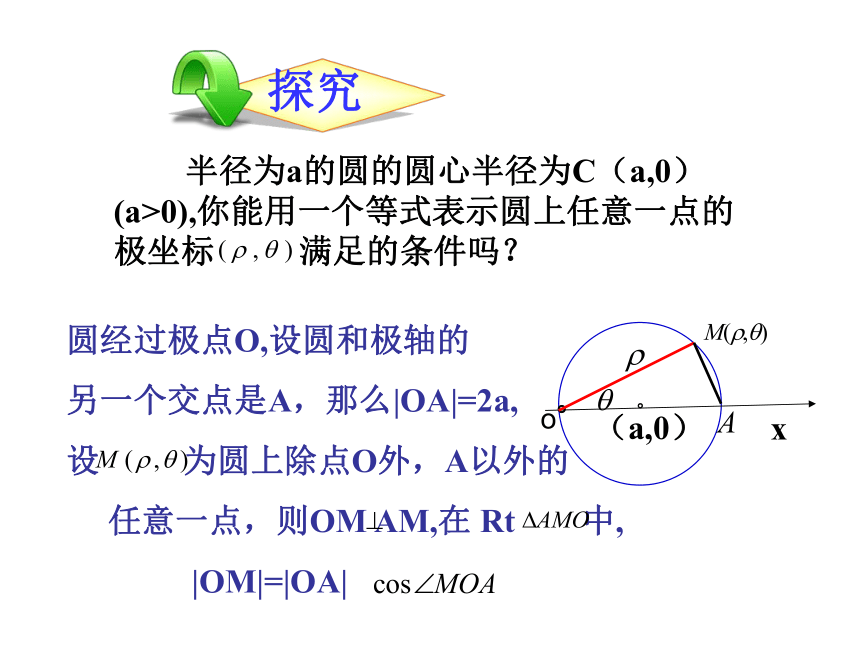
半径为a的圆的圆心半径为C(a,0)(a>0),你能用一个等式表示圆上任意一点的极坐标 满足的条件吗?
。
x
(a,0)
o
。
圆经过极点O,设圆和极轴的
另一个交点是A,那么|OA|=2a,
设 为圆上除点O外,A以外的
任意一点,则OM AM,在 Rt 中,
|OM|=|OA|
即
(1)
等式(1)是圆上任意一点的极坐标满足的条件
曲线的极坐标方程定义:
如果曲线C上的点与方程f(?,?)=0有如下关系
(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(?,?)=0 ;
(2)方程f(?,?)=0的所有解为坐标,的点都在曲线C上,则曲线C的方程是f(?,?)=0。
例1.已知圆O的半径为r,建立怎样的极坐标系,可以使圆的极坐标方程更简单?
解:如果以圆心O为极点,
从O出发的一条射线为极轴建立坐标系,
那么圆上各点的几何特征就是它们
的极径都等于半径r,设 为
圆上任意一点,则|MO|=r,即
1.求下列圆的极坐标方程
(1)圆的中心在极点,半径为3,
(2)中心在点A(a,0),半径为a,
(3)中心在点(b,?/2),半径为b,
(4)中心在点B(?1,?1),半径为r。
?=2
?=2acos ?
?=2bsin ?
2.以极坐标系中的点(1,1)为圆心,半径为1的圆的方程是
3.曲线 关于极轴对称的曲线是
( C )
( C )
4.极坐标方程分别是ρ=cosθ和
ρ=sinθ的两个圆的圆心距是( )
5.下列极坐标方程各表示什么图形?
表示圆心在极点,半径为4的圆;
表示过极点,圆心在 半径为1的圆
直线 经过极点,从极轴到直线
的角是 ,求直线 的极坐标
方程.
X
O
)
)
M
X
O
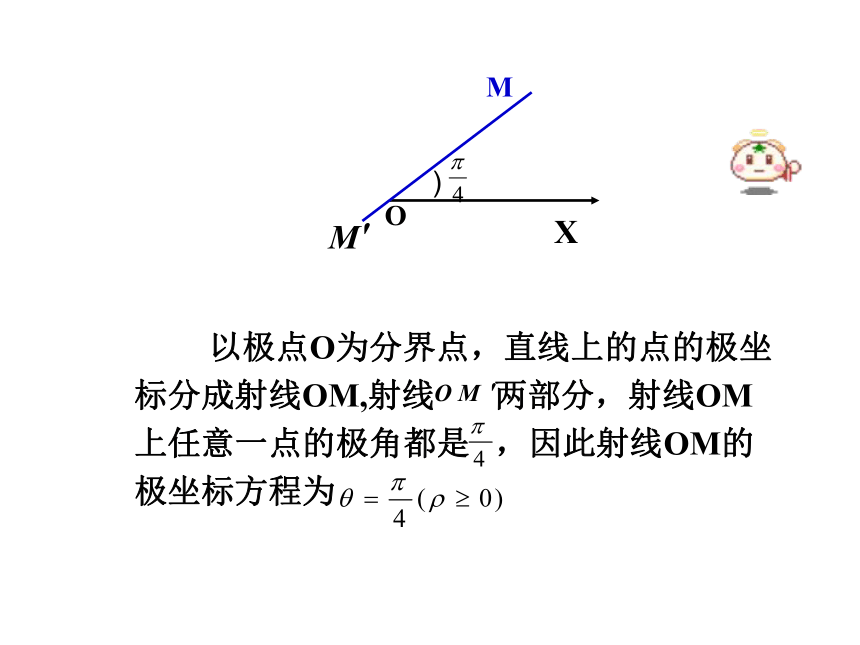
以极点O为分界点,直线上的点的极坐标分成射线OM,射线 两部分,射线OM上任意一点的极角都是 ,因此射线OM的极坐标方程为
)
M
X
O
射线OM上任意一点的极角为
即射线 的
极坐标方程为
即直线的极坐标方程为
或
例1.求过点A(a,0)(a>0),且垂直于极轴的直线的极坐标方程。
)
0
a
A
X
M
解:设M( , )为直线上
除A外的任意一点,连接 OM,在三角形MOA中,
即
(1)
式(1)就是所求直线的极坐标方程
解 题 基 本 步 骤
第一步:根据题意画出草图;
第二步:设M( ,)是直线上任意一点;
第三步:连接MO;
第四步:根据几何条件建立关于 ,
的方程,并化简;
第五步:检验并确认所得的方程即为所求。
例2.设点P的极坐标 直线
过点P且与极轴所成的角为 ,
求直线 的极坐标方程。
若 则 我们规定点 与点 关于极点对称
解:设 为直线上
除了点P 外的任意一点,
连接OM,|OM|= , =
由题意得,
|OP|= ,
设直线与极轴交于点A, 则
在 中, ,
X
M
O
)
)
由正弦定理得
即
因此直线的极坐标方程为
X
M
O
)
)
例3.把下列的直角坐标方程化为极坐标方程
(1)2x+6y-1=0 (2)x2 -y2=25
解:将公式 代入
所给的直角坐标方程中,得
化简得
1.将下列直角坐标方程化成极坐标方程系
2.将下列极坐标方程化为直角坐标方程
1.圆的极坐标方程的概念;
2.如何求圆的极坐标方程;
3.会将直角坐标方程化为极坐标方程;
4.直线的极坐标方程的几种情况:
(1)过极点
(2)过某个定点,且垂直于极轴
(3)过某个定点,且与极轴成一定的角度
1(2017年高考)线 ,所围成的图形面积是( )
和
D
2.解:
5.解:以极点为直角坐标原点,极轴为X轴正半轴建立平面直角坐标系,把直线的极坐标方程。
化为直角坐标方程,得
把点A 的极坐标化为
直角坐标,得
在平面直角坐标系中,由点到直线
的距离公式,得点A 到直线
的距离
所以点A到这条直线的距离为
6.解 :(1)以椭圆中心O为直角坐标原点,长轴所在的直线为X轴建立直角坐标系,则椭圆的直角坐标方程为
将椭圆的直角坐标方程化为极坐标方程,
得
由于 可设
则
于是
(2)依题意,得到
所以 为定值
当且仅当 时,即 或
时, 有最小值
当 ,即 或 时,
有最大值
1.3.1圆的极坐标方程
1.3.2直线的极坐标方程
在直角坐标系中,平面曲线C可以用
方程 表示,类似的,在极坐
标系中,是否也可以用方程表示?
新课导入
半径为a的圆的圆心半径为C(a,0)(a>0),你能用一个等式表示圆上任意一点的极坐标 满足的条件吗?
。
x
(a,0)
o
。
圆经过极点O,设圆和极轴的
另一个交点是A,那么|OA|=2a,
设 为圆上除点O外,A以外的
任意一点,则OM AM,在 Rt 中,
|OM|=|OA|
即
(1)
等式(1)是圆上任意一点的极坐标满足的条件
曲线的极坐标方程定义:
如果曲线C上的点与方程f(?,?)=0有如下关系
(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(?,?)=0 ;
(2)方程f(?,?)=0的所有解为坐标,的点都在曲线C上,则曲线C的方程是f(?,?)=0。
例1.已知圆O的半径为r,建立怎样的极坐标系,可以使圆的极坐标方程更简单?
解:如果以圆心O为极点,
从O出发的一条射线为极轴建立坐标系,
那么圆上各点的几何特征就是它们
的极径都等于半径r,设 为
圆上任意一点,则|MO|=r,即
1.求下列圆的极坐标方程
(1)圆的中心在极点,半径为3,
(2)中心在点A(a,0),半径为a,
(3)中心在点(b,?/2),半径为b,
(4)中心在点B(?1,?1),半径为r。
?=2
?=2acos ?
?=2bsin ?
2.以极坐标系中的点(1,1)为圆心,半径为1的圆的方程是
3.曲线 关于极轴对称的曲线是
( C )
( C )
4.极坐标方程分别是ρ=cosθ和
ρ=sinθ的两个圆的圆心距是( )
5.下列极坐标方程各表示什么图形?
表示圆心在极点,半径为4的圆;
表示过极点,圆心在 半径为1的圆
直线 经过极点,从极轴到直线
的角是 ,求直线 的极坐标
方程.
X
O
)
)
M
X
O
以极点O为分界点,直线上的点的极坐标分成射线OM,射线 两部分,射线OM上任意一点的极角都是 ,因此射线OM的极坐标方程为
)
M
X
O
射线OM上任意一点的极角为
即射线 的
极坐标方程为
即直线的极坐标方程为
或
例1.求过点A(a,0)(a>0),且垂直于极轴的直线的极坐标方程。
)
0
a
A
X
M
解:设M( , )为直线上
除A外的任意一点,连接 OM,在三角形MOA中,
即
(1)
式(1)就是所求直线的极坐标方程
解 题 基 本 步 骤
第一步:根据题意画出草图;
第二步:设M( ,)是直线上任意一点;
第三步:连接MO;
第四步:根据几何条件建立关于 ,
的方程,并化简;
第五步:检验并确认所得的方程即为所求。
例2.设点P的极坐标 直线
过点P且与极轴所成的角为 ,
求直线 的极坐标方程。
若 则 我们规定点 与点 关于极点对称
解:设 为直线上
除了点P 外的任意一点,
连接OM,|OM|= , =
由题意得,
|OP|= ,
设直线与极轴交于点A, 则
在 中, ,
X
M
O
)
)
由正弦定理得
即
因此直线的极坐标方程为
X
M
O
)
)
例3.把下列的直角坐标方程化为极坐标方程
(1)2x+6y-1=0 (2)x2 -y2=25
解:将公式 代入
所给的直角坐标方程中,得
化简得
1.将下列直角坐标方程化成极坐标方程系
2.将下列极坐标方程化为直角坐标方程
1.圆的极坐标方程的概念;
2.如何求圆的极坐标方程;
3.会将直角坐标方程化为极坐标方程;
4.直线的极坐标方程的几种情况:
(1)过极点
(2)过某个定点,且垂直于极轴
(3)过某个定点,且与极轴成一定的角度
1(2017年高考)线 ,所围成的图形面积是( )
和
D
2.解:
5.解:以极点为直角坐标原点,极轴为X轴正半轴建立平面直角坐标系,把直线的极坐标方程。
化为直角坐标方程,得
把点A 的极坐标化为
直角坐标,得
在平面直角坐标系中,由点到直线
的距离公式,得点A 到直线
的距离
所以点A到这条直线的距离为
6.解 :(1)以椭圆中心O为直角坐标原点,长轴所在的直线为X轴建立直角坐标系,则椭圆的直角坐标方程为
将椭圆的直角坐标方程化为极坐标方程,
得
由于 可设
则
于是
(2)依题意,得到
所以 为定值
当且仅当 时,即 或
时, 有最小值
当 ,即 或 时,
有最大值
