人教新课标A版选修4-4第二章 参数方程 圆锥曲线的参数方程(共35张PPT)
文档属性
| 名称 | 人教新课标A版选修4-4第二章 参数方程 圆锥曲线的参数方程(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 22:15:56 | ||
图片预览







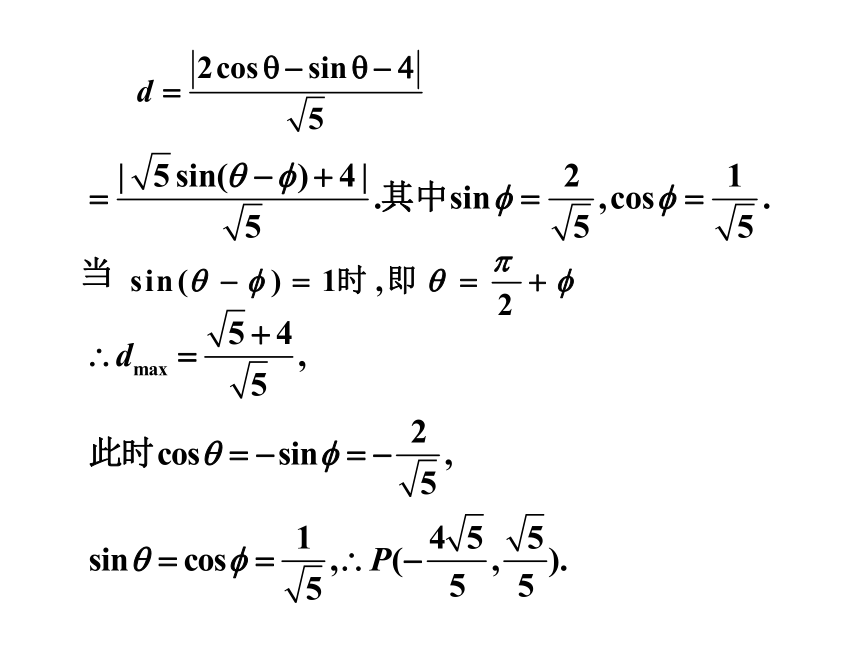




文档简介
(共35张PPT)
前几节课我们学习了圆
的参数方程是 那么,对于椭圆
,它的参数方程用什么来表示呢?
导入新课
从几何变换的角度看,通过伸缩变换
椭圆 可以变成
圆 ,利用圆的参数方程
可以得到椭圆的参数方程为:
1.如图,以原点O为圆心,
分别以a,b(a>b >0)为半径,作两个同心圆,
点B是大圆半径OA与小圆的交点,过点A作
,垂足为N.过点B作
,垂足为M,求当半径
OA绕点0旋转时,点M的
轨迹的参数方程.
解:设点M的坐标为(x,y), 是以
为始边,OA为终边的正角,取 为参数.
那么,
即所求点M的轨迹参数方程为.
这是中心在原点O,焦点在X轴上的椭圆
2.求椭圆 上的点P到直线
的最大距离及此时P点的坐标.
解:由已知,可得椭圆的参数方程为
∵椭圆上的点
到直线 的距离
当
1.在椭圆 上求一点P,使P
到直线 的距离最小.
课堂练习
P的坐标为
类似于探究椭圆参数方程的方法我们
来探究双曲线
的参数方程.
导入新课
如图,以原点O为圆心,a,b(a>0,b>0)为半径
分别作同心圆C1,C2.
设A为圆C1上任意
一点,作直线OA,
过点A作圆C1的
切线 与X轴交于
点 ,过圆C2与
x轴的交点B作切线 与直线OA交于点 .
过点 分别作y轴,x轴的平行线
交于点M.
设OX为始边,
OA为终边的角为
,点M的坐
标为(x,y),那么
点 的坐标为(x,0)
点 的坐标为(b,y).
因为点A在圆上,所以点A的坐标为
所以
因为
所以
从而
这是中心在原点,焦点在X轴上的双曲线,
通常规定参数 的范围是
且
1.设M为双曲线
上任意一点,O为原点,
过M作双曲线两渐渐线,
分别与两渐渐线交于A,B两点,
求平行四边形MAOB的面积,
由此得出什么结论?
y
解:双曲线的渐渐线方程为
设M为双曲线右支上一点,
其坐标为 ,
其直线MA的方程为
将 代入此方程,解得点A的横坐标为,
y
同理可得,点B的横坐标为
设 则
因此平行四边形MAOB的面积为
因此,平行四边形的面积恒为定值, 与点M在双曲线上的位置无关.
y
1.设双曲线 (a>0,b>0)
的渐近线与抛物线y=x2 +1相切,则该双曲线的
离心率等于( )
A、 B、2 C、 D、
C
课堂练习
2.求证:双曲线
上任一点P到两渐近线距离之积为定值
前面曾经得到以时刻t作参数的抛物线的参数方程:
( 为参数且 )
想想对于一般的抛物线,建立怎样相应的
参数方程呢?
导入新课
如图,设抛物线的普通方程
y=2px , P点表示焦点到
准线的距离,设M(x,y)为抛物线除顶点外的一点,以射线OM为终边的角记为
由三角函数 定义可得:
解得,
这就是抛物线的参数方程.
令 ,
则有,抛物线y2=2px的参数方程为
( 为参数)
当t=0,此参数方程表示抛物线的顶点(0,0),因此,当
此参数方程表示整条抛物线,参数t
表示抛物线上除顶点外的任意一点
与原点连线的斜率的倒数.
1.如图,
A,B是抛物
上异于顶点的两动点,
且 ,
并与AB相交于点M,
求点M的轨迹方程.
y
0
解:根据条件,设点M,A,B的坐标分别为
则
因为 所以
即
所以
(2019年全国)
1.已知椭圆 的右焦点为 ,
右准线为 ,点 ,线段 交C于点
若 ,则 =( )
A、 B、2
C、 D、3
A
解:过点B作 于M,并设右准线 与X轴的交点为N,易知FN=1.由题意,
故 .又由椭圆的第二定义,得:
,故选A
2.设双曲线 (a>0,b>0)的渐近
线与抛物线y=x2 +1相切,则该双曲线的离心率
等于( )
A、 B、2 C、 D、
C
(2019年辽宁)
解:设切点 ,则切线的斜率为
.由题意有
又
解得, .
3.已知直线
与抛物线 相交于A,B两点,F为C
的焦点,若 则 ( )
A、 B、 C、 D、
(2017年海南)
D
2017年(理工农医类)(北京卷)
4.已知双曲线 的离心率为
右准线方程为
(Ⅰ)求双曲线的方程;
(Ⅱ)设直线 是圆 上动点
处的切线,
与双曲线交于不同的两点 ,
证明的 大小为定值.
解:(Ⅰ)由题意,得,
解得,
∴ ,
∴所求双曲线的方程为
(Ⅱ)点 在圆 上,
圆在点 处的切线方程为
化简得
由
及
得,
∵切线 与双曲线C交于不同的两点A、B, 且,
∴ 且
设A、B两点的坐标分别为
则,
又
所以 的大小为90°
且
前几节课我们学习了圆
的参数方程是 那么,对于椭圆
,它的参数方程用什么来表示呢?
导入新课
从几何变换的角度看,通过伸缩变换
椭圆 可以变成
圆 ,利用圆的参数方程
可以得到椭圆的参数方程为:
1.如图,以原点O为圆心,
分别以a,b(a>b >0)为半径,作两个同心圆,
点B是大圆半径OA与小圆的交点,过点A作
,垂足为N.过点B作
,垂足为M,求当半径
OA绕点0旋转时,点M的
轨迹的参数方程.
解:设点M的坐标为(x,y), 是以
为始边,OA为终边的正角,取 为参数.
那么,
即所求点M的轨迹参数方程为.
这是中心在原点O,焦点在X轴上的椭圆
2.求椭圆 上的点P到直线
的最大距离及此时P点的坐标.
解:由已知,可得椭圆的参数方程为
∵椭圆上的点
到直线 的距离
当
1.在椭圆 上求一点P,使P
到直线 的距离最小.
课堂练习
P的坐标为
类似于探究椭圆参数方程的方法我们
来探究双曲线
的参数方程.
导入新课
如图,以原点O为圆心,a,b(a>0,b>0)为半径
分别作同心圆C1,C2.
设A为圆C1上任意
一点,作直线OA,
过点A作圆C1的
切线 与X轴交于
点 ,过圆C2与
x轴的交点B作切线 与直线OA交于点 .
过点 分别作y轴,x轴的平行线
交于点M.
设OX为始边,
OA为终边的角为
,点M的坐
标为(x,y),那么
点 的坐标为(x,0)
点 的坐标为(b,y).
因为点A在圆上,所以点A的坐标为
所以
因为
所以
从而
这是中心在原点,焦点在X轴上的双曲线,
通常规定参数 的范围是
且
1.设M为双曲线
上任意一点,O为原点,
过M作双曲线两渐渐线,
分别与两渐渐线交于A,B两点,
求平行四边形MAOB的面积,
由此得出什么结论?
y
解:双曲线的渐渐线方程为
设M为双曲线右支上一点,
其坐标为 ,
其直线MA的方程为
将 代入此方程,解得点A的横坐标为,
y
同理可得,点B的横坐标为
设 则
因此平行四边形MAOB的面积为
因此,平行四边形的面积恒为定值, 与点M在双曲线上的位置无关.
y
1.设双曲线 (a>0,b>0)
的渐近线与抛物线y=x2 +1相切,则该双曲线的
离心率等于( )
A、 B、2 C、 D、
C
课堂练习
2.求证:双曲线
上任一点P到两渐近线距离之积为定值
前面曾经得到以时刻t作参数的抛物线的参数方程:
( 为参数且 )
想想对于一般的抛物线,建立怎样相应的
参数方程呢?
导入新课
如图,设抛物线的普通方程
y=2px , P点表示焦点到
准线的距离,设M(x,y)为抛物线除顶点外的一点,以射线OM为终边的角记为
由三角函数 定义可得:
解得,
这就是抛物线的参数方程.
令 ,
则有,抛物线y2=2px的参数方程为
( 为参数)
当t=0,此参数方程表示抛物线的顶点(0,0),因此,当
此参数方程表示整条抛物线,参数t
表示抛物线上除顶点外的任意一点
与原点连线的斜率的倒数.
1.如图,
A,B是抛物
上异于顶点的两动点,
且 ,
并与AB相交于点M,
求点M的轨迹方程.
y
0
解:根据条件,设点M,A,B的坐标分别为
则
因为 所以
即
所以
(2019年全国)
1.已知椭圆 的右焦点为 ,
右准线为 ,点 ,线段 交C于点
若 ,则 =( )
A、 B、2
C、 D、3
A
解:过点B作 于M,并设右准线 与X轴的交点为N,易知FN=1.由题意,
故 .又由椭圆的第二定义,得:
,故选A
2.设双曲线 (a>0,b>0)的渐近
线与抛物线y=x2 +1相切,则该双曲线的离心率
等于( )
A、 B、2 C、 D、
C
(2019年辽宁)
解:设切点 ,则切线的斜率为
.由题意有
又
解得, .
3.已知直线
与抛物线 相交于A,B两点,F为C
的焦点,若 则 ( )
A、 B、 C、 D、
(2017年海南)
D
2017年(理工农医类)(北京卷)
4.已知双曲线 的离心率为
右准线方程为
(Ⅰ)求双曲线的方程;
(Ⅱ)设直线 是圆 上动点
处的切线,
与双曲线交于不同的两点 ,
证明的 大小为定值.
解:(Ⅰ)由题意,得,
解得,
∴ ,
∴所求双曲线的方程为
(Ⅱ)点 在圆 上,
圆在点 处的切线方程为
化简得
由
及
得,
∵切线 与双曲线C交于不同的两点A、B, 且,
∴ 且
设A、B两点的坐标分别为
则,
又
所以 的大小为90°
且
