数学必修3第3章概率章末复习(共28张PPT)
文档属性
| 名称 | 数学必修3第3章概率章末复习(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 482.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 21:52:12 | ||
图片预览







文档简介
(共28张PPT)
第三章 概率
3.3 几何概型
3.2 古典概型
3.1 随机事件的概率
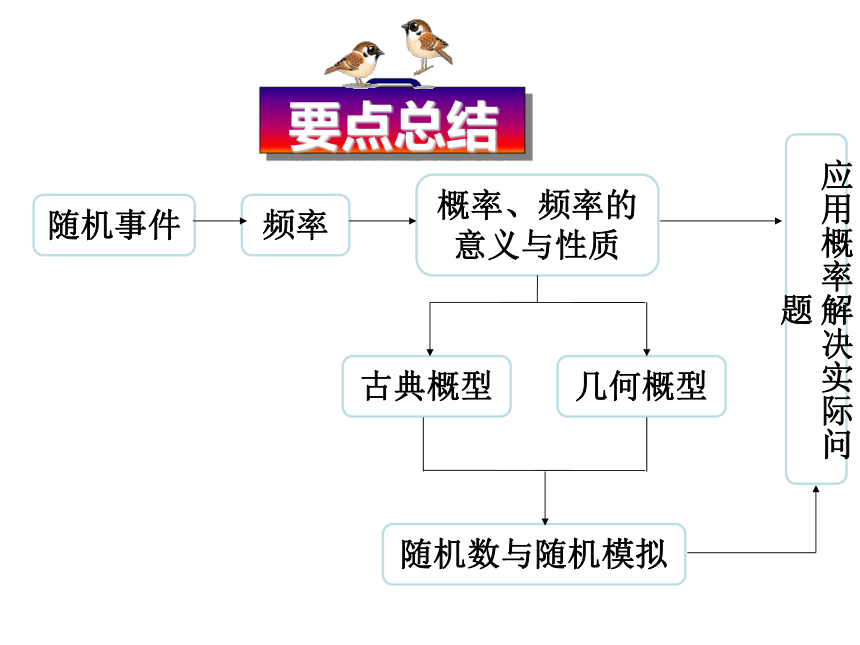
首先掌握概率的基本概念,理解随机事件的实验,在这基础上应用概率的基本性质,结合古典概型和几何概型解决实际问题。应注意古典概型和几何概型的区别。
(1)必然事件:在条件S下,一定会发生的事件,叫相对于条件S的必然事件;
(2)不可能事件:在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;
(3)确定事件:必然事件和不可能事件统称为相对于条件S的确定事件;
(4)随机事件:在条件S下可能发生也可能不发生的事件,叫相对于条件S的随机事件;
3.1.1 -3.1.2随机事件的概率及概率的意义
(5)频数与频率:在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数;称事件A出现的
比例fn(A)= 为事件A出现的概率:对于给定
的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率。
(6)频率与概率的区别与联系:随机事件的频率,指此事件发生的次数nA与试验总次数n的比值
它具有一定的稳定性,总在某个常数附近摆动,
且随着试验次数的不断增多,这种摆动幅度越来越小。我们把这个常数叫做随机事件的概率,概率从数量上反映了随机事件发生的可能性的大小。频率在大量重复试验的前提下可以近似地作为这个事件的概率。
(1)概率与公平性的关系:
利用概率解释游戏规则的公平性,判断实际生活中的一些现象是否合理。
概率在实际问题中的应用:
(2)概率与决策的关系:
在“风险与决策”中经常会用到统计中的极大似然法:在一次实验中,概率大的事件发生的可能性大。
(3)概率与预报的关系:
在对各种自然现象、灾害的研究过程中经常会用到概率的思想来进行预测。
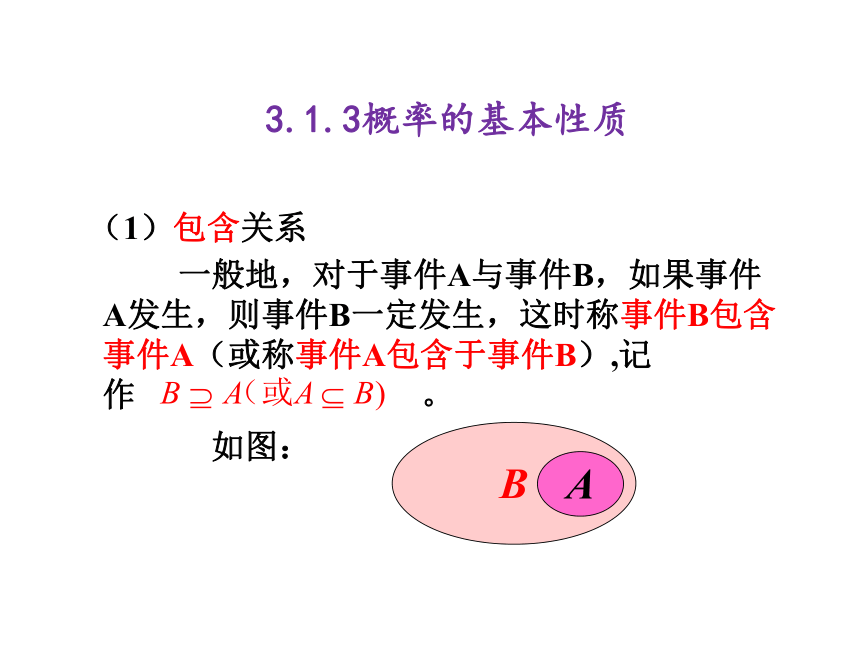
3.1.3概率的基本性质
B
如图:
(1)包含关系
A
(2)相等关系
如图:
B
A
(3)并事件(和事件)
如图:
(4)交事件(积事件)
B
A
如图:
(5)互斥事件
A
B
如图:
(6)互为对立事件
如图:
如果事件 A 与事件 B 互斥,则
概率的加法公式:
特别地,如果事件 A 与事件 B 是互为对立事件,则
3.2 古典概型
掷一枚质地均匀的硬币,结果只有2个,即“正面朝上”或“反面朝上”,它们都是随机事件。
我们把这类随机事件成为基本事件。
基本事件的特点:
任何两个基本事件是互斥的;
任何事件都可以表示成基本事件的和。
(1) 试验总所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概率。
对于古典概型,任何事件的概率为:
P(A)= A包含的基本事件的个数
基本事件的总数
3.2 几何概型
几何概率模型:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型。
几何概型的概率公式:
P(A)=
几何概型的特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等。
1.随机事件的概率;
2.古典概型;
3.与统计一起出第二道大题的可能性比较;大。也有可能出一道选择题或填空题。
(1)概率的概念以及在实例中的应用;
(2)两种概率模型的计算公式;
(3)对随机现象的理解。
1,掷两枚骰子,求事件A为出现的点数之和等于3的概率?
错解:
掷两枚骰子出现的点数之和的可能数值为{2、3、…、12}
有利于事件A的结果只有3,故P(A)=1/11
基本事件总数:36
有利于事件A的结果数:2
P(A)=1/18
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
2,从10件产品(其中3件次品)中,一件一件地不放回地任意取出4件,求4件中恰有一件次品的概率。
错解:
因为第一次有10种取法,第二次有9种取法…,由乘法原理可知从10件取4件共有10×9×8×7种取法,故样本空间S中基本事件总数有10×9×8×7个。
设A=“取出4件中恰有一件次品”,则A中含有 种取法。
错解:
因为第一次有10种取法,第二次有9种取法…,由乘法原理可知从10件取4件共有10×9×8×7种取法,故样本空间S中基本事件总数有10×9×8×7个。
设A=“取出4件中恰有一件次品”,则A中含有 种取法。
正解2:(都用组合方法)
样本空间S中含有 个基本事件,
事件A中包含 个基本事件。
第三章 概率
3.3 几何概型
3.2 古典概型
3.1 随机事件的概率
首先掌握概率的基本概念,理解随机事件的实验,在这基础上应用概率的基本性质,结合古典概型和几何概型解决实际问题。应注意古典概型和几何概型的区别。
(1)必然事件:在条件S下,一定会发生的事件,叫相对于条件S的必然事件;
(2)不可能事件:在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;
(3)确定事件:必然事件和不可能事件统称为相对于条件S的确定事件;
(4)随机事件:在条件S下可能发生也可能不发生的事件,叫相对于条件S的随机事件;
3.1.1 -3.1.2随机事件的概率及概率的意义
(5)频数与频率:在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数;称事件A出现的
比例fn(A)= 为事件A出现的概率:对于给定
的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率。
(6)频率与概率的区别与联系:随机事件的频率,指此事件发生的次数nA与试验总次数n的比值
它具有一定的稳定性,总在某个常数附近摆动,
且随着试验次数的不断增多,这种摆动幅度越来越小。我们把这个常数叫做随机事件的概率,概率从数量上反映了随机事件发生的可能性的大小。频率在大量重复试验的前提下可以近似地作为这个事件的概率。
(1)概率与公平性的关系:
利用概率解释游戏规则的公平性,判断实际生活中的一些现象是否合理。
概率在实际问题中的应用:
(2)概率与决策的关系:
在“风险与决策”中经常会用到统计中的极大似然法:在一次实验中,概率大的事件发生的可能性大。
(3)概率与预报的关系:
在对各种自然现象、灾害的研究过程中经常会用到概率的思想来进行预测。
3.1.3概率的基本性质
B
如图:
(1)包含关系
A
(2)相等关系
如图:
B
A
(3)并事件(和事件)
如图:
(4)交事件(积事件)
B
A
如图:
(5)互斥事件
A
B
如图:
(6)互为对立事件
如图:
如果事件 A 与事件 B 互斥,则
概率的加法公式:
特别地,如果事件 A 与事件 B 是互为对立事件,则
3.2 古典概型
掷一枚质地均匀的硬币,结果只有2个,即“正面朝上”或“反面朝上”,它们都是随机事件。
我们把这类随机事件成为基本事件。
基本事件的特点:
任何两个基本事件是互斥的;
任何事件都可以表示成基本事件的和。
(1) 试验总所有可能出现的基本事件只有有限个;
(2) 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概率。
对于古典概型,任何事件的概率为:
P(A)= A包含的基本事件的个数
基本事件的总数
3.2 几何概型
几何概率模型:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型。
几何概型的概率公式:
P(A)=
几何概型的特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等。
1.随机事件的概率;
2.古典概型;
3.与统计一起出第二道大题的可能性比较;大。也有可能出一道选择题或填空题。
(1)概率的概念以及在实例中的应用;
(2)两种概率模型的计算公式;
(3)对随机现象的理解。
1,掷两枚骰子,求事件A为出现的点数之和等于3的概率?
错解:
掷两枚骰子出现的点数之和的可能数值为{2、3、…、12}
有利于事件A的结果只有3,故P(A)=1/11
基本事件总数:36
有利于事件A的结果数:2
P(A)=1/18
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
2,从10件产品(其中3件次品)中,一件一件地不放回地任意取出4件,求4件中恰有一件次品的概率。
错解:
因为第一次有10种取法,第二次有9种取法…,由乘法原理可知从10件取4件共有10×9×8×7种取法,故样本空间S中基本事件总数有10×9×8×7个。
设A=“取出4件中恰有一件次品”,则A中含有 种取法。
错解:
因为第一次有10种取法,第二次有9种取法…,由乘法原理可知从10件取4件共有10×9×8×7种取法,故样本空间S中基本事件总数有10×9×8×7个。
设A=“取出4件中恰有一件次品”,则A中含有 种取法。
正解2:(都用组合方法)
样本空间S中含有 个基本事件,
事件A中包含 个基本事件。
