5.4 平移课件
图片预览








文档简介
(共29张PPT)
人教版 七年级数学下
5.4 平移
学习目标
1.通过实例了解平移的概念;
2.理解并掌握平移的性质及决定因素;(重点、难点)
3.能按要求做出平移后的图像。(重点)
小小竹排江中游,巍巍青山两岸走-----
情境导入
情境导入
大厦里的电梯
这些图片有什么共同特点?
物体沿着一定的方向直线移动了一段距离。
产品在传送带上缓缓移动。
合作探究---平移的定义及性质
仔细观察下列美丽的图案,回答问题:
(1) 这些图案有什么共同特点?
(2)下面这些图案能否根据其中一部分绘制整个图案?若能,你
能否想象出是怎么绘制的?
思考1:如何在一张半透明的纸上,画出一排形状和大小如图5.4-2的雪人呢?
合作探究---平移的定义及性质
可以把一张半透明的纸盖在图5.4-2上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如图5.4-3)
图5.4-3
合作探究---平移的定义及性质
思考2:如图5.4-4,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A?,冒顶B与B?,纽扣C与C?),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
图5.4-4
合作探究---平移的定义及性质
合作探究
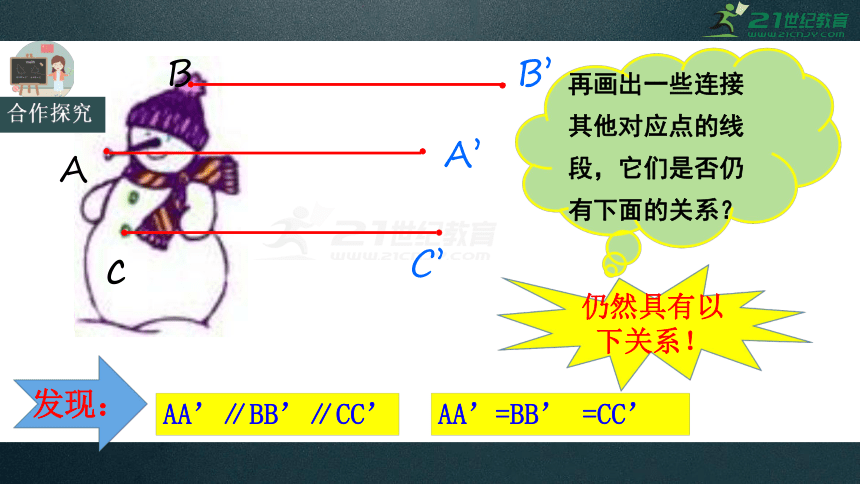
AA’∥BB’∥CC’
AA’=BB’ =CC’
A
A’
B
B’
C’
c
发现:
合作探究
再画出一些连接其他对应点的线段,它们是否仍有下面的关系?
仍然具有以下关系!
A
B
C
E
F
D
直线
距离
平移的定义: 在平面内,将一个图形整体沿某一 __ 方向移动一定的 ___ ,得到一个新图形,图形的这种移动,叫做平移变换,简称平移.
性质特征:
(1)平移不改变图形的形状和大小;
(3)对应点连线平行(或在同一条直线上)且相等。
(2)只改变了图形的位置;
合作探究---平移的定义及性质
如图,其中A与D、B与E、C与F是对应点; A到D的方向是三角形的平移方向;线段 AD的长度是平移的距离。
(4)对应线段平行(或在同一条直线上)且相等,对应角相等。
小试牛刀
1.以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
2.将左图中的图案平移后,可以得到的图案是( )
A.①② B.①③ C.②③ D.②④
D
A
知识点拨:①、 ③中涉及的是旋转运动。
合作探究
3、如图1,示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是( )
A.∠F,AC B.∠BOD,BA
C.∠F,BA D.∠BOD,AC
4、如图2所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=__ 度,∠EDF=__ 度,
∠F=____度,∠DOB=____度.
C
70
50
60
60
合作探究---平移的决定因素
思考3: (1)图形平移的方向一定是水平或竖直的吗?
(2)图形平移后的位置由什么确定?
(1)图形平移的方向不一定是水平的,也不一定是竖直的;
(2)图形平移的位置由平移的方向和距离决定.
合作探究---平移后图像的画法
作平移后的图形 :
A
B
● D
1、 平移线段AB,使点A平移到D点的位置,你能作出线段AB平移的图形DE吗?
解(1)连接AD,
(2)过点D作AB的平行线, 在上截取DE=AB.
DE即为所求。
● E
2、如图1,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
解:(1)连接 ,
(2)过点B作AA’的平行线, 在上截取BB’= ,
(3)过点 作 的平行线,在上截
取CC’= ,
(4)连接A’B’,B’C’,A’C’,所得的三角
形就是平移后的三角形.
AA’
AA’
C
AA’
AA’
B’
C’
合作探究---平移后图像的画法
1.确定平移方向,
2.确定移动距离,
3.寻找图形的关键点,
4.顺次连接对应点即可。
按某个条件对一个图形进行平移要注意:
小结:如何进行平移作图
合作探究---平移后图像的画法
小试牛刀
1、将图中的小船向左平移6格.
小试牛刀
小试牛刀
D
F
3、如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,
请画出点A的对应点D、点C的对应点F的位置,连接△DEF.
小试牛刀---能力提升
4.某宾馆在重新装修后,准备在大厅的楼梯上铺上某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图28-4所示,则购买地毯至少需要 ________元.
504
课堂总结
1、平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
2、平移的性质: 平移不改变图形的形状和大小。经过平移,对应点所连的线段平行(或在同一条直线上)且相等;对应线段平行(或在同一条直线上)且相等,对应角相等。
3、决定平移的因素:平移的方向和距离.
4、图形平移的画法:①.确定平移方向,②.确定移动距离,
③.寻找图形的关键点,④.顺次连接对应点即可。
本节课你有哪些收获?
综合演练
1、下列生活中的物体的运动情况可以看成平移的是( )
A、篮球运动员投篮时篮球的运动
B、飞机在跑道上滑行到停止的运动
C、空中放飞的风筝的运动
D、冷水加热过程中小气泡上升变为大气泡
B
知识点拨:A、B中的篮球和风筝不是沿直线移动,因此不是平移;D中
的气泡在上升过程中大小发生了变化,根据平移的性质可以判断也不是
平移。
综合演练
2.下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
C
知识点拨:图形在移动过程中,不会出现不动点,图形上的所有点都
在随着图形的一定而移动。
综合演练
3.如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为( )
A.6 B.8 C.10 D.12
C
C D
知识点拨:连接BD,取BF的中点H,连接DH。通过平移可知A与D、B与F是
对应点,根据平移的性质可知BF ∥ CD, BF = CD,再由AC=CD,点H是BE
的中点可知AC=CD=BH=HF,所以△ABC、 △BCD、 △BDH、 △HDF、 △DEF
是等底等高的三角形,进而面积是相等的,所以答案是10.
H
综合演练
4、如图所示,已知正方形的边长为4 cm,把它沿AB方向平移3 cm,求平移后两个正方形重叠部分的面积 .
D
A
C
B
E
F
4(cm2)
知识点拨:BF=4-3=1(cm).
S=BC×BF
=4×1
=4(cm2).
综合演练
1m
21m
15m
A
C
D
B
5、如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
解:长草部分的面积=(21-1)×15
=300(m2).
知识点拨:平移构成规则图形。
解:长草部分的面积=(21-1)×15=300(m2).
综合演练
6.如何将平行四边形ABCD平移,使点A移动到点E,画出平移后的图形.
E
A
B
C
D
F
G
H
四边形 EFGH 就是四边形ABCD平移后的图形.
课后作业
课本教材第30页:3、4、6题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级数学下
5.4 平移
学习目标
1.通过实例了解平移的概念;
2.理解并掌握平移的性质及决定因素;(重点、难点)
3.能按要求做出平移后的图像。(重点)
小小竹排江中游,巍巍青山两岸走-----
情境导入
情境导入
大厦里的电梯
这些图片有什么共同特点?
物体沿着一定的方向直线移动了一段距离。
产品在传送带上缓缓移动。
合作探究---平移的定义及性质
仔细观察下列美丽的图案,回答问题:
(1) 这些图案有什么共同特点?
(2)下面这些图案能否根据其中一部分绘制整个图案?若能,你
能否想象出是怎么绘制的?
思考1:如何在一张半透明的纸上,画出一排形状和大小如图5.4-2的雪人呢?
合作探究---平移的定义及性质
可以把一张半透明的纸盖在图5.4-2上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如图5.4-3)
图5.4-3
合作探究---平移的定义及性质
思考2:如图5.4-4,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A?,冒顶B与B?,纽扣C与C?),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
图5.4-4
合作探究---平移的定义及性质
合作探究
AA’∥BB’∥CC’
AA’=BB’ =CC’
A
A’
B
B’
C’
c
发现:
合作探究
再画出一些连接其他对应点的线段,它们是否仍有下面的关系?
仍然具有以下关系!
A
B
C
E
F
D
直线
距离
平移的定义: 在平面内,将一个图形整体沿某一 __ 方向移动一定的 ___ ,得到一个新图形,图形的这种移动,叫做平移变换,简称平移.
性质特征:
(1)平移不改变图形的形状和大小;
(3)对应点连线平行(或在同一条直线上)且相等。
(2)只改变了图形的位置;
合作探究---平移的定义及性质
如图,其中A与D、B与E、C与F是对应点; A到D的方向是三角形的平移方向;线段 AD的长度是平移的距离。
(4)对应线段平行(或在同一条直线上)且相等,对应角相等。
小试牛刀
1.以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
2.将左图中的图案平移后,可以得到的图案是( )
A.①② B.①③ C.②③ D.②④
D
A
知识点拨:①、 ③中涉及的是旋转运动。
合作探究
3、如图1,示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是( )
A.∠F,AC B.∠BOD,BA
C.∠F,BA D.∠BOD,AC
4、如图2所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=__ 度,∠EDF=__ 度,
∠F=____度,∠DOB=____度.
C
70
50
60
60
合作探究---平移的决定因素
思考3: (1)图形平移的方向一定是水平或竖直的吗?
(2)图形平移后的位置由什么确定?
(1)图形平移的方向不一定是水平的,也不一定是竖直的;
(2)图形平移的位置由平移的方向和距离决定.
合作探究---平移后图像的画法
作平移后的图形 :
A
B
● D
1、 平移线段AB,使点A平移到D点的位置,你能作出线段AB平移的图形DE吗?
解(1)连接AD,
(2)过点D作AB的平行线, 在上截取DE=AB.
DE即为所求。
● E
2、如图1,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
解:(1)连接 ,
(2)过点B作AA’的平行线, 在上截取BB’= ,
(3)过点 作 的平行线,在上截
取CC’= ,
(4)连接A’B’,B’C’,A’C’,所得的三角
形就是平移后的三角形.
AA’
AA’
C
AA’
AA’
B’
C’
合作探究---平移后图像的画法
1.确定平移方向,
2.确定移动距离,
3.寻找图形的关键点,
4.顺次连接对应点即可。
按某个条件对一个图形进行平移要注意:
小结:如何进行平移作图
合作探究---平移后图像的画法
小试牛刀
1、将图中的小船向左平移6格.
小试牛刀
小试牛刀
D
F
3、如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,
请画出点A的对应点D、点C的对应点F的位置,连接△DEF.
小试牛刀---能力提升
4.某宾馆在重新装修后,准备在大厅的楼梯上铺上某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图28-4所示,则购买地毯至少需要 ________元.
504
课堂总结
1、平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
2、平移的性质: 平移不改变图形的形状和大小。经过平移,对应点所连的线段平行(或在同一条直线上)且相等;对应线段平行(或在同一条直线上)且相等,对应角相等。
3、决定平移的因素:平移的方向和距离.
4、图形平移的画法:①.确定平移方向,②.确定移动距离,
③.寻找图形的关键点,④.顺次连接对应点即可。
本节课你有哪些收获?
综合演练
1、下列生活中的物体的运动情况可以看成平移的是( )
A、篮球运动员投篮时篮球的运动
B、飞机在跑道上滑行到停止的运动
C、空中放飞的风筝的运动
D、冷水加热过程中小气泡上升变为大气泡
B
知识点拨:A、B中的篮球和风筝不是沿直线移动,因此不是平移;D中
的气泡在上升过程中大小发生了变化,根据平移的性质可以判断也不是
平移。
综合演练
2.下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
C
知识点拨:图形在移动过程中,不会出现不动点,图形上的所有点都
在随着图形的一定而移动。
综合演练
3.如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为( )
A.6 B.8 C.10 D.12
C
C D
知识点拨:连接BD,取BF的中点H,连接DH。通过平移可知A与D、B与F是
对应点,根据平移的性质可知BF ∥ CD, BF = CD,再由AC=CD,点H是BE
的中点可知AC=CD=BH=HF,所以△ABC、 △BCD、 △BDH、 △HDF、 △DEF
是等底等高的三角形,进而面积是相等的,所以答案是10.
H
综合演练
4、如图所示,已知正方形的边长为4 cm,把它沿AB方向平移3 cm,求平移后两个正方形重叠部分的面积 .
D
A
C
B
E
F
4(cm2)
知识点拨:BF=4-3=1(cm).
S=BC×BF
=4×1
=4(cm2).
综合演练
1m
21m
15m
A
C
D
B
5、如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
解:长草部分的面积=(21-1)×15
=300(m2).
知识点拨:平移构成规则图形。
解:长草部分的面积=(21-1)×15=300(m2).
综合演练
6.如何将平行四边形ABCD平移,使点A移动到点E,画出平移后的图形.
E
A
B
C
D
F
G
H
四边形 EFGH 就是四边形ABCD平移后的图形.
课后作业
课本教材第30页:3、4、6题
https://www.21cnjy.com/help/help_extract.php
