湘教版八年级数学下册课件1.2.3 勾股定理的逆定理(16张PPT)
文档属性
| 名称 | 湘教版八年级数学下册课件1.2.3 勾股定理的逆定理(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 12:54:02 | ||
图片预览






文档简介
课件16张PPT。第一章
直角三角形八年级数学湘教版·下册1.2.3 勾股定理的逆定理学习目标
1.掌握直角三角形的判定定理.(重点)
2.掌握勾股数的概念.
3.能够运用勾股定理的逆定理解决问题.(难点)新课导入 问题:同学们你们知道古埃及人用什么方法得到直角吗? 用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第9个结,拉紧绳子就得到一个直角三角形,其直角在第4个结处.新知探究 问题1:下面有三组数分别是一个三角形的三边长a,b,c,
①5,12,13; ②7,24,25; ③8,15,17.
回答下列问题:
1.这三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?新知探究实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2,可以构成直角三角形.新知探究问题2:从上述问题中,能发现什么结论吗? 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.有同学认为测量结果可能有误差,不同意这个发现.你觉得这个发现正确吗?你能给
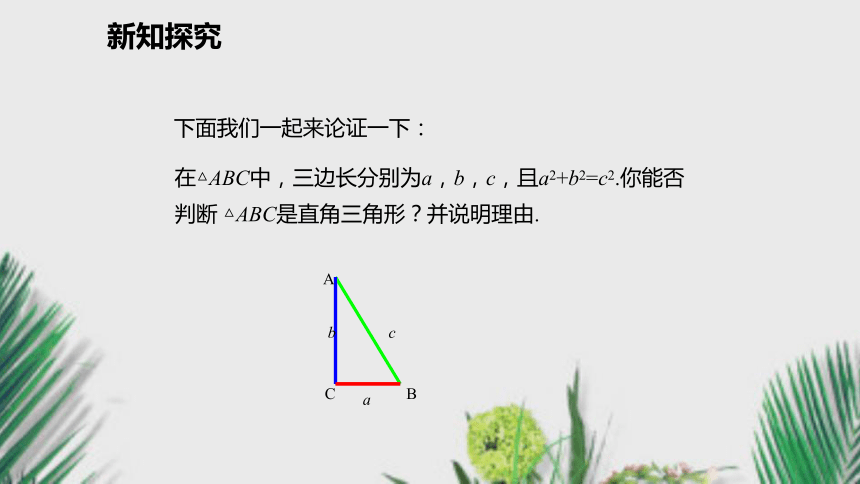
出一个更有说服力的理由吗?新知探究在△ABC中,三边长分别为a,b,c,且a2+b2=c2.你能否判断 △ABC是直角三角形?并说明理由.下面我们一起来论证一下:acACB新知探究简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.在Rt△A1C1B1中,由勾股定理,得A1B12=a2+b2=AB2 .
∴ A1B1=AB,∴ △ABC ≌△A1B1C1 (SSS).
∴ ∠C=∠C1=90°,
∴ △ABC是直角三角形.acbACB新知探究典例精析例1:一个零件的形状如图1所示,按规定这个零件中∠A
和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如
图2所示,这个零件符合要求吗?DABC4351312DABC图1图2新知探究在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
新知探究如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
满足a2+b2=c2的三个正整数,称为勾股数.
概念学习新知探究例2:下列各组数是勾股数的是( ) .
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132
A 方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.课堂小结勾股定理的逆定理如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.勾股数:满足a2+b2=c2的三个正整数.课堂小测1. 如果线段a,b,c能组成直角三角形,则它们的比可
以是 ( ) .
A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5将直角三角形的三边长扩大同样的倍数,则得到的
三角形 ( ) .
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形BA 课堂小测4.如果三条线段a,b,c满足a2=c2-b2,这三条线段组成的
三角形是直角三角形吗?为什么?解:是直角三角形.因为a2+b2=c2满足勾股定理的逆定理.3.以△ABC的三条边为边长向外作正方形, 依次得到的面
积是25, 144 , 169, 则这个三角形是______三角形.直角课堂小测5.如图,在正方形ABCD中,AB=4,AE=2,DF=1, 图中有几个直角三角形,你是如何判断的? 与你的同伴交流.解:△ABE,△DEF,△FCB均为直角三角形.
由勾股定理,
知BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25,
∴BE2+EF2=BF2,
∴ △BEF是直角三角形.CABDEF
1.掌握直角三角形的判定定理.(重点)
2.掌握勾股数的概念.
3.能够运用勾股定理的逆定理解决问题.(难点)新课导入 问题:同学们你们知道古埃及人用什么方法得到直角吗? 用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第9个结,拉紧绳子就得到一个直角三角形,其直角在第4个结处.新知探究 问题1:下面有三组数分别是一个三角形的三边长a,b,c,
①5,12,13; ②7,24,25; ③8,15,17.
回答下列问题:
1.这三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?新知探究实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2,可以构成直角三角形.新知探究问题2:从上述问题中,能发现什么结论吗? 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.有同学认为测量结果可能有误差,不同意这个发现.你觉得这个发现正确吗?你能给
出一个更有说服力的理由吗?新知探究在△ABC中,三边长分别为a,b,c,且a2+b2=c2.你能否判断 △ABC是直角三角形?并说明理由.下面我们一起来论证一下:acACB新知探究简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.在Rt△A1C1B1中,由勾股定理,得A1B12=a2+b2=AB2 .
∴ A1B1=AB,∴ △ABC ≌△A1B1C1 (SSS).
∴ ∠C=∠C1=90°,
∴ △ABC是直角三角形.acbACB新知探究典例精析例1:一个零件的形状如图1所示,按规定这个零件中∠A
和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如
图2所示,这个零件符合要求吗?DABC4351312DABC图1图2新知探究在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
新知探究如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
满足a2+b2=c2的三个正整数,称为勾股数.
概念学习新知探究例2:下列各组数是勾股数的是( ) .
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132
A 方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.课堂小结勾股定理的逆定理如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.勾股数:满足a2+b2=c2的三个正整数.课堂小测1. 如果线段a,b,c能组成直角三角形,则它们的比可
以是 ( ) .
A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5将直角三角形的三边长扩大同样的倍数,则得到的
三角形 ( ) .
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形BA 课堂小测4.如果三条线段a,b,c满足a2=c2-b2,这三条线段组成的
三角形是直角三角形吗?为什么?解:是直角三角形.因为a2+b2=c2满足勾股定理的逆定理.3.以△ABC的三条边为边长向外作正方形, 依次得到的面
积是25, 144 , 169, 则这个三角形是______三角形.直角课堂小测5.如图,在正方形ABCD中,AB=4,AE=2,DF=1, 图中有几个直角三角形,你是如何判断的? 与你的同伴交流.解:△ABE,△DEF,△FCB均为直角三角形.
由勾股定理,
知BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25,
∴BE2+EF2=BF2,
∴ △BEF是直角三角形.CABDEF
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
