湘教版八年级数学下册课件1.3直角三角形全等的判定(12张PPT)
文档属性
| 名称 | 湘教版八年级数学下册课件1.3直角三角形全等的判定(12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 12:56:06 | ||
图片预览





文档简介
课件12张PPT。第一章
直角三角形八年级数学湘教版·下册1.3 直角三角形全等的判定学习目标
1.探索并理解直角三角形全等的判定方法“HL”.(难点)
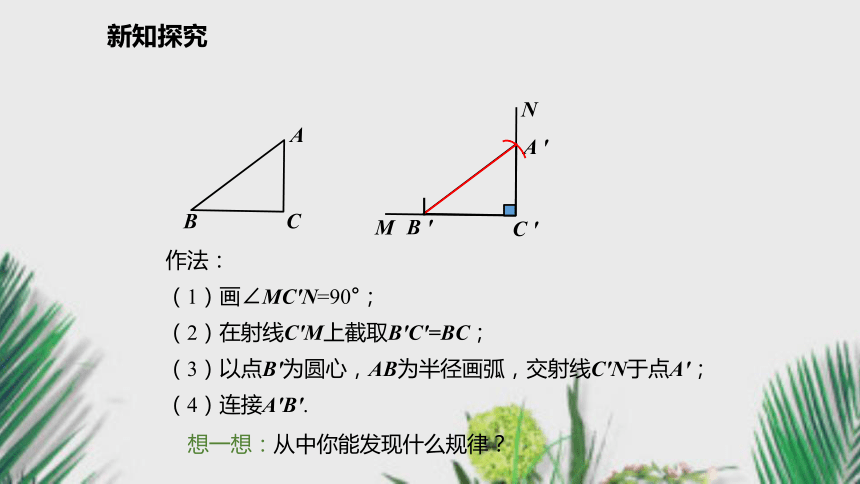
2.会用直角三角形全等的判定方法“HL”判定两个直角三 角形全等.(重点)新课导入 2.判别两个三角形全等的方法: SSS ASAAASSAS1.全等三角形的性质:对应角相等,对应边相等.复习引入新知探究AAA3.SSA新知探究 任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们全等吗?新知探究A ′ B ′ 作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.想一想:从中你能发现什么规律?新知探究“斜边、直角边”判定方法文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).几何语言:∴在Rt△ABC和Rt△ A′B′C′ 中,∴Rt△ABC ≌ Rt△ A′B′C′ (HL).∵∠C=∠C′=90°,新知探究 例: 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC ﹦AD.证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.在 Rt△ABC 和Rt△BAD 中,∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD(全等三角形的对应边相等).课堂小结“斜边、直角边”内容斜边和一条直角边对应相等的两个直角三角形全等.前提条件在直角三角形中.使用方法 只须找除直角外的两个条件即可
(两个条件中至少有一个条件是一对对应边相等).课堂小测1. 如图,∠B=∠D=90°,要证明△ABC 与△ADC全等,
还需要补充的条件是 (写出一个即可).答案: AB=AD 或 BC=DC 或
∠BAC=∠DAC 或 ∠ACB=∠ACD.C课堂小测2.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.
求证:△EBC≌△DCB.证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.在 Rt△EBC 和Rt△DCB 中,∴ Rt△EBC≌Rt△DCB (HL).课堂小测3.如图,AB=CD,BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.证明: ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在Rt△ABF和Rt△CDE中,
∴ Rt△ABF ≌Rt△CDE(HL),∴BF=DE.
1.探索并理解直角三角形全等的判定方法“HL”.(难点)
2.会用直角三角形全等的判定方法“HL”判定两个直角三 角形全等.(重点)新课导入 2.判别两个三角形全等的方法: SSS ASAAASSAS1.全等三角形的性质:对应角相等,对应边相等.复习引入新知探究AAA3.SSA新知探究 任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们全等吗?新知探究A ′ B ′ 作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.想一想:从中你能发现什么规律?新知探究“斜边、直角边”判定方法文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).几何语言:∴在Rt△ABC和Rt△ A′B′C′ 中,∴Rt△ABC ≌ Rt△ A′B′C′ (HL).∵∠C=∠C′=90°,新知探究 例: 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC ﹦AD.证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.在 Rt△ABC 和Rt△BAD 中,∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD(全等三角形的对应边相等).课堂小结“斜边、直角边”内容斜边和一条直角边对应相等的两个直角三角形全等.前提条件在直角三角形中.使用方法 只须找除直角外的两个条件即可
(两个条件中至少有一个条件是一对对应边相等).课堂小测1. 如图,∠B=∠D=90°,要证明△ABC 与△ADC全等,
还需要补充的条件是 (写出一个即可).答案: AB=AD 或 BC=DC 或
∠BAC=∠DAC 或 ∠ACB=∠ACD.C课堂小测2.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.
求证:△EBC≌△DCB.证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.在 Rt△EBC 和Rt△DCB 中,∴ Rt△EBC≌Rt△DCB (HL).课堂小测3.如图,AB=CD,BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.证明: ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在Rt△ABF和Rt△CDE中,
∴ Rt△ABF ≌Rt△CDE(HL),∴BF=DE.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
