2020年春人教版七年级数学下册 5.1相交线 同步习题(基础类)(解析版)
文档属性
| 名称 | 2020年春人教版七年级数学下册 5.1相交线 同步习题(基础类)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 21:21:32 | ||
图片预览

文档简介
5.1相交线 同步基础习题
一.选择题(共15小题)
1.在如图图形中,线段PQ能表示点P到直线L的距离的是( )
A. B.
C. D.
2.如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )
A.35° B.45° C.55° D.65°
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B.
C. D.
4.下面的四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
5.如图,同位角是( )
A.∠1和∠2 B.∠3和∠4 C.∠2和∠4 D.∠1和∠4
6.如图,直线AB⊥CD于点O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.互为余角 B.互为补角 C.互为对顶角 D.互为邻补角
7.如图,已知直线a,b被直线c所截,那么∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
8.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM等于( )
A.140° B.120° C.100° D.80°
9.如图,描述同位角、内错角、同旁内角关系不正确的是( )
A.∠1与∠4是同位角 B.∠2与∠3是内错角
C.∠3与∠4是同旁内角 D.∠2与∠4是同旁内角
10.如图,下列说法错误的是( )
A.∠A与∠C是同旁内角 B.∠1与∠3是同位角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
11.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是( )
A.两点之间线段最短
B.过两点有且只有一条直线
C.垂线段最短
D.过一点可以作无数条直线
12.下列说法中,正确的是( )
A.相等的角是对顶角
B.有公共顶点,并且相等的角是对顶角
C.如果∠1与∠2是对顶角,那么∠1=∠2
D.两条直线相交所成的两个角是对顶角
13.下列哪种方法不能检验直线与水平面是否垂直( )
A.铅垂线 B.两块三角尺 C.长方形纸片 D.合页型折纸
14.如图,CO⊥AB于点O,DE经过点O,∠COD=50°,则∠AOE为( )
A.30° B.40° C.50° D.60°
15.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
二.填空题(共10小题)
16.如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 .
17.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= .
18.如图所示:直线AB与CD相交于O,已知∠1=30°,OE是∠BOC的平分线,则∠2= °,∠3= °.
19.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB,理由 .
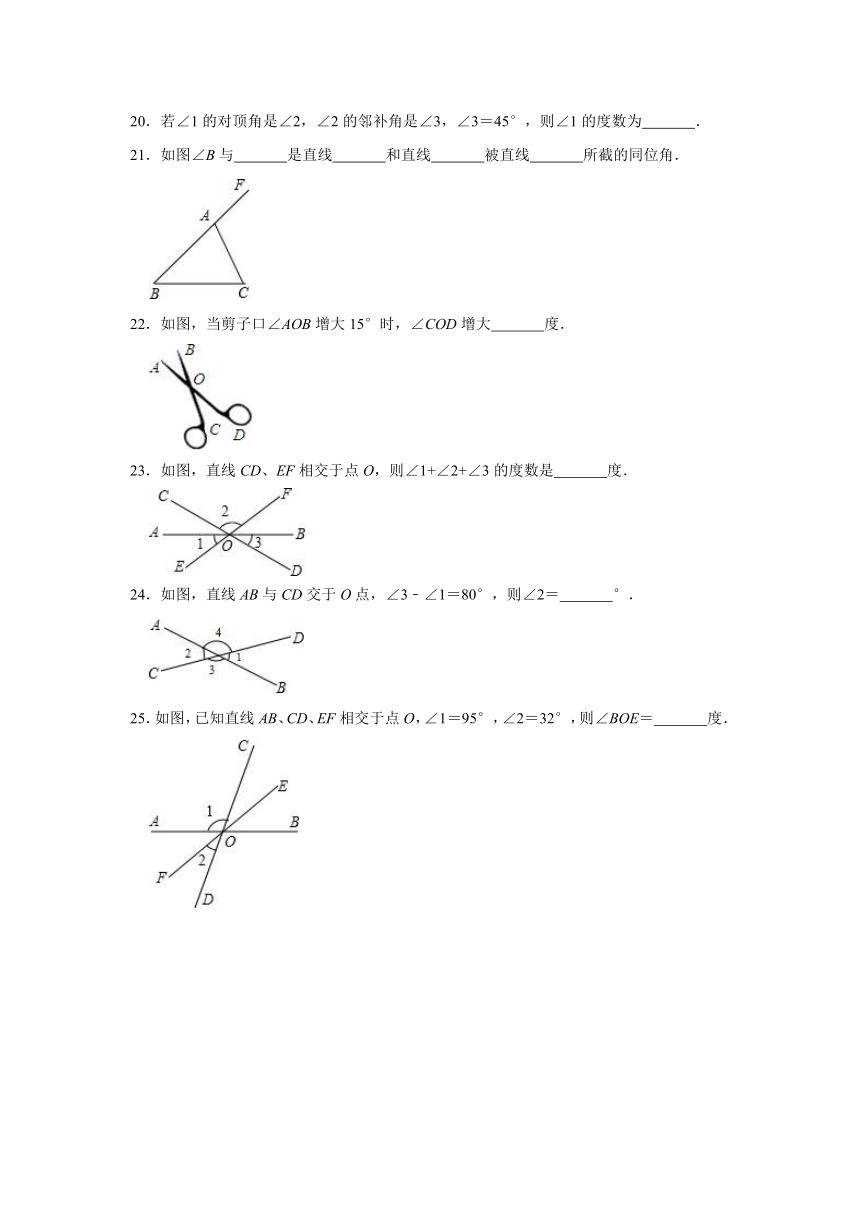
20.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为 .
21.如图∠B与 是直线 和直线 被直线 所截的同位角.
22.如图,当剪子口∠AOB增大15°时,∠COD增大 度.
23.如图,直线CD、EF相交于点O,则∠1+∠2+∠3的度数是 度.
24.如图,直线AB与CD交于O点,∠3﹣∠1=80°,则∠2= °.
25.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 度.
5.1相交线 同步基础习题
参考答案
一.选择题(共15小题)
1.在如图图形中,线段PQ能表示点P到直线L的距离的是( )
A. B.
C. D.
【分析】根据直线外一点到这条直线的垂线段的长度,叫做点到直线的距离的概念判断.
【解答】解:图A、B、C中,线段PQ不与直线L垂直,故线段PQ不能表示点P到直线L的距离;
图D中,线段PQ与直线L垂直,垂足为点Q,故线段PQ能表示点P到直线L的距离;
故选:D.
2.如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )
A.35° B.45° C.55° D.65°
【分析】根据垂线的定义,可得∠COD,根据角的和差,可得答案.
【解答】解:∵OC⊥OD,
∴∠COD=90°.
由角的和差,得
∠2=180°﹣∠COD﹣∠1
=180°﹣90°﹣35°=55°,
故选:C.
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B.
C. D.
【分析】根据点到直线的距离是指垂线段的长度,即可解答.
【解答】解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
4.下面的四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的定义作出判断即可.
【解答】解:根据对顶角的定义可知:只有C图中的∠1与∠2是对顶角,其它都不是.
故选:C.
5.如图,同位角是( )
A.∠1和∠2 B.∠3和∠4 C.∠2和∠4 D.∠1和∠4
【分析】根据同位角定义:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角进行分析即可.
【解答】解:图中∠1和∠4是同位角,
故选:D.
6.如图,直线AB⊥CD于点O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.互为余角 B.互为补角 C.互为对顶角 D.互为邻补角
【分析】根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余,从而求解.
【解答】解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°.
故选:A.
7.如图,已知直线a,b被直线c所截,那么∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
【解答】解:∠1的内错角是∠3.
故选:B.
8.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM等于( )
A.140° B.120° C.100° D.80°
【分析】先根据对顶角相等得出∠AOC﹣80°,再根据角平分线的定义得出∠COM,最后解答即可.
【解答】解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°,
故选:A.
9.如图,描述同位角、内错角、同旁内角关系不正确的是( )
A.∠1与∠4是同位角 B.∠2与∠3是内错角
C.∠3与∠4是同旁内角 D.∠2与∠4是同旁内角
【分析】利用同位角、内错角、同旁内角的定义判定即可.
【解答】解:A、∠1与∠4是同位角,故A选项正确;
B、∠2与∠3是内错角,故B选项正确;
C、∠3与∠4是同旁内角,故C选项正确;
D、∠2与∠4是同旁内角,故D选项错误.
故选:D.
10.如图,下列说法错误的是( )
A.∠A与∠C是同旁内角 B.∠1与∠3是同位角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
【分析】根据同位角、内错角、同旁内角的定义,可得答案.
【解答】解:A、∠A与∠C是同旁内角,故A正确;
B、∠1与∠3是同旁内角,故B错误;
C、∠2与∠3是内错角,故C正确;
D、∠3与∠B是同旁内角,故D正确;
故选:B.
11.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是( )
A.两点之间线段最短
B.过两点有且只有一条直线
C.垂线段最短
D.过一点可以作无数条直线
【分析】根据垂线段的性质:垂线段最短进行解答即可.
【解答】解:这样做的理由是根据垂线段最短.
故选:C.
12.下列说法中,正确的是( )
A.相等的角是对顶角
B.有公共顶点,并且相等的角是对顶角
C.如果∠1与∠2是对顶角,那么∠1=∠2
D.两条直线相交所成的两个角是对顶角
【分析】根据对顶角的定义与对顶角相等的性质对各选项分析判断后利用排除法求解.
【解答】解:A、对顶角相等,但相等的角不一定是对顶角,故本选项错误;
B、有公共顶点,并且相等的角是对顶角错误,故本选项错误;
C、如果∠1与∠2是对顶角,那么∠1=∠2正确,故本选项正确;
D、两条直线相交所成的四个角有两对对顶角,故本选项错误.
故选:C.
13.下列哪种方法不能检验直线与水平面是否垂直( )
A.铅垂线 B.两块三角尺 C.长方形纸片 D.合页型折纸
【分析】直线与水平面垂直,必须满足直线垂直于水平面内两条相交的直线,由此作出判断.
【解答】解:A、根据重力学原理,铅垂线垂直于水平面;
B、将两块三角板的直角边重合,另外两条直角边相交,放在水平面上,可判断重合的直角边垂直于水平面;
C、长方形纸片只能判断长与宽互相垂直,不能判断与水平面垂直;
D、合页型折纸其折痕与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把两放到水平面上,可判断折痕与水平面垂直;
故选:C.
14.如图,CO⊥AB于点O,DE经过点O,∠COD=50°,则∠AOE为( )
A.30° B.40° C.50° D.60°
【分析】由已知条件和观察图形可知∠COD与∠DOB互余,∠DOB与∠AOE是对顶角,利用这些关系可解此题.
【解答】解:∵CO⊥AB,
∴∠COB=90°,
又∵∠COD=50°,
∴∠DOB=90°﹣50°=40°,
∴∠AOE=∠DOB=40°,
故选:B.
15.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90
【分析】利用对顶角相等,可知∠1+∠2+∠3的和是360°的一半.
【解答】解:因为对顶角相等,所以∠1+∠2+∠3=×360°=180°.
故选:B.
二.填空题(共10小题)
16.如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 垂线段最短 .
【分析】根据垂线段的性质,可得答案.
【解答】解:要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短,
故答案为:垂线段最短.
17.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= 40° .
【分析】根据角平分线的定义求出∠AOC,再根据对顶角相等解答.
【解答】解:∵OA平分∠EOC,∠EOC=80°,
∴∠AOC=∠EOC=×80°=40°,
∴∠BOD=∠AOC=40°.
故答案为:40°.
18.如图所示:直线AB与CD相交于O,已知∠1=30°,OE是∠BOC的平分线,则∠2= 30 °,∠3= 75 °.
【分析】根据对顶角相等求出∠2,根据邻补角求出∠BOC,根据角平分线定义求出∠3即可.
【解答】解:∵∠1=30°,
∴∠2=∠1=30°,∠BOC=180°﹣∠1=150°,
∵OE是∠BOC的平分线,
∴∠3=∠BOC=75°,
故答案为:30,75.
19.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB,理由 垂线段最短 .
【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.据此作答.
【解答】解:根据垂线段定理,连接直线外一点与直线上所有点的连线中,垂线段最短,
∵PB⊥AD,
∴PB最短.
故答案为:垂线段最短.
20.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为 135° .
【分析】根据对顶角相等、邻补角互补的性质求解.
【解答】解:∵∠2的邻补角是∠3,∠3=45°,
∴∠2=180°﹣∠3=135°.
∵∠1的对顶角是∠2,
∴∠1=∠2=135°.
21.如图∠B与 ∠FAC 是直线 AC 和直线 BC 被直线 FB 所截的同位角.
【分析】两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.据此作答.
【解答】解:根据图象,∠B与∠FAC是直线AC和直线BC被直线FB所截的同位角,所以应填∠FAC,AC,BC,FB.
22.如图,当剪子口∠AOB增大15°时,∠COD增大 15 度.
【分析】根据对顶角的定义和性质求解.
【解答】解:因为∠AOB与∠COD是对顶角,∠AOB与∠COD始终相等,所以随∠AOB变化,∠COD也发生同样变化.
故当剪子口∠AOB增大15°时,∠COD也增大15°.
23.如图,直线CD、EF相交于点O,则∠1+∠2+∠3的度数是 180 度.
【分析】要求∠1+∠2+∠3的度数,由对顶角相等,可得∠2=∠EOD,所以所求度数等于∠1+∠EOD+∠3的度数,即等于180°.
【解答】解:∵∠2=∠EOD,
∴∠1+∠2+∠3=∠1+∠EOD+∠3=180°.
24.如图,直线AB与CD交于O点,∠3﹣∠1=80°,则∠2= 50 °.
【分析】先由邻补角的定义,得∠1+∠3=180°,结合已知求出∠1的度数,再根据对顶角相等得∠2的度数.
【解答】解:∵∠3﹣∠1=80°,
又∵∠1+∠3=180°,
∴解得∠1=50°,
∴∠2=∠1=50°.
25.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE= 53 度.
【分析】由∠BOE与∠AOF是对顶角,可得∠BOE=∠AOF,又因为∠COD是平角,可得∠1+∠2+∠AOF=180°,将∠1=95°,∠2=32°代入,即可求得∠AOF的度数,即∠BOE的度数.
【解答】解:∵∠BOE与∠AOF是对顶角,
∴∠BOE=∠AOF,
∵∠1=95°,∠2=32°,∠COD是平角,
∴∠AOF=180°﹣∠1﹣∠2=180°﹣95°﹣32°=53°,
即∠BOE=53°.
