第六章万有引力定律-典型例题
文档属性
| 名称 | 第六章万有引力定律-典型例题 |

|
|
| 格式 | zip | ||
| 文件大小 | 161.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-03 00:00:00 | ||
图片预览



文档简介
万有引力定律-典型例题
典型例题1——关于开普勒的三大定律
??月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天。应用开普勒定律计算:在赤道平面内离地面多少高度,人造地球卫星可以随地球一起转动,就像停留在无空中不动一样.
??分析:月球和人造地球卫星都在环绕地球运动,根据开普勒第三定律,它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的.
??解:设人造地球卫星运行半径为R,周期为T,根据开普勒第三定律有:
??同理设月球轨道半径为 ,周期为 ,也有:
??由以上两式可得:
??在赤道平面内离地面高度:
km
??点评:随地球一起转动,就好像停留在天空中的卫星,通常称之为定点卫星.它们离地面的高度是一个确定的值,不能随意变动。
典型例题2——利用月相求解月球公转周期
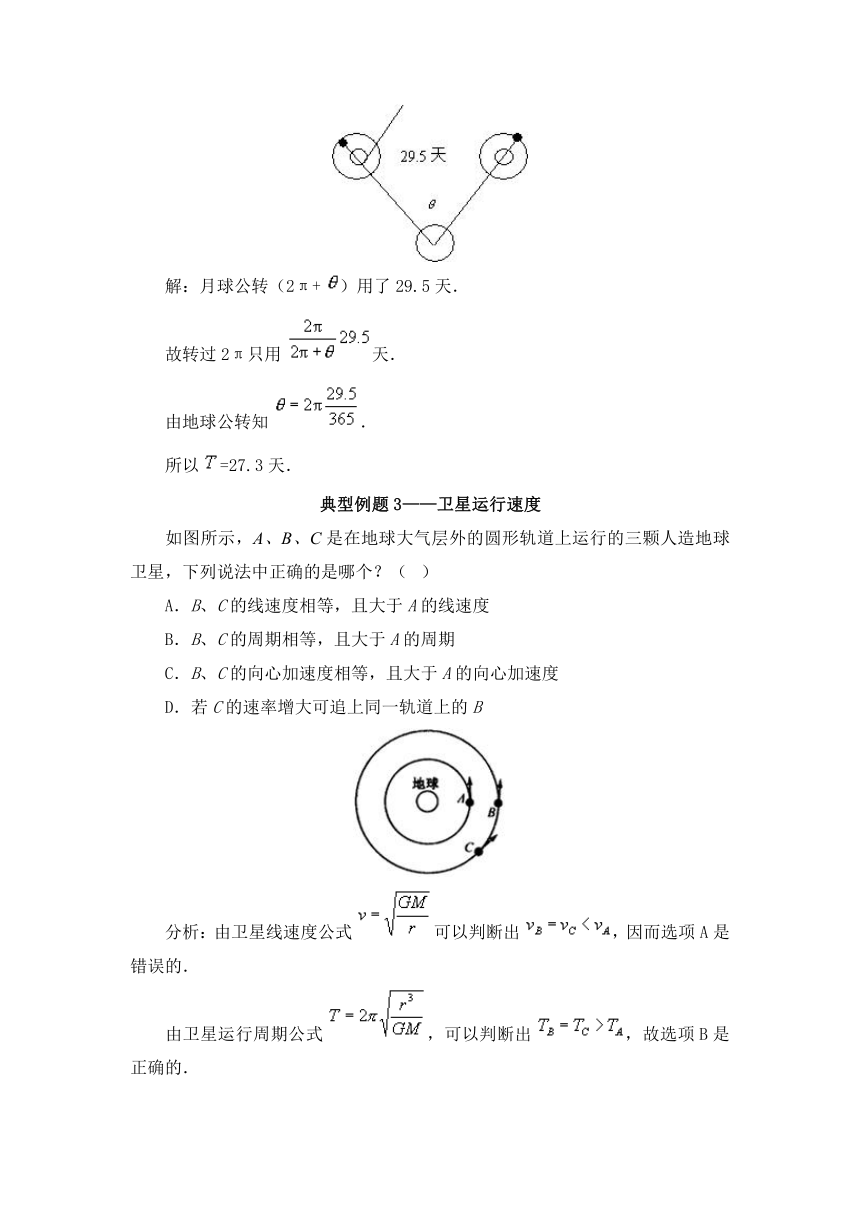
??若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内,且都为正圆.又知这两种转动同向,如图所示,月相变化的周期为29.5天(图是相继两次满月,月、地、日相对位置示意图).
??解:月球公转(2π+ )用了29.5天.
??故转过2π只用 天.
??由地球公转知 .
??所以 =27.3天.
典型例题3——卫星运行速度
??如图所示,A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星,下列说法中正确的是哪个?(? )
??A.B、C的线速度相等,且大于A的线速度
??B.B、C的周期相等,且大于A的周期
??C.B、C的向心加速度相等,且大于A的向心加速度
??D.若C的速率增大可追上同一轨道上的B
??分析:由卫星线速度公式 可以判断出 ,因而选项A是错误的.
??由卫星运行周期公式 ,可以判断出 ,故选项B是正确的.
??卫星的向心加速度是万有引力作用于卫星上产生的,由 ,可知 , 因而选项C是错误的.
??若使卫星C速率增大,则必然会导致卫星C偏离原轨道,它不可能追上卫星B,故D也是错误的.
??解:本题正确选项为B。
??点评:由于人造地球卫星在轨道上运行时,所需要的向心力是由万有引力提供的,若由于某种原因,使卫星的速度增大。则所需要的向心力也必然会增加,而万有引力在轨道不变的时候,是不可能增加的,这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。
典型例题4——星体质量的求解
??已知地球表面的重力加速度为 ,地球半径为 ,万有引力恒量为 ,用以上各量表示,地球质量为 是多少?
??解:由
??得:
典型例题5——星体密度的求解
??已知地球表面的重力加速度为 ,地球半径为 ,万有引力恒量为 ,如果不考虑地球自转的影响,用以上各量表示,地球的平均密度是多少?
??解:
??由万有引力定律得:
??得:
典型例题6——证明星体密度与周期平方乘积为常量
??行星的平均密度是 ,靠近行星表面的卫星的周期是T,试证明 为一个常数.
??分析:将行星看作一个球体,卫星绕行星做匀速圆周运动的问心力由万有引力提供.
??解:设半径为R,则密度 为质量M与体积之比:
即:
??对卫星,万有引力等于向心力
所以:
即:
??因为G为引力常量,所以 是一个对任何行星都适用的常数.
??点评:从本题结论可以看出,若能观察到某行星附近的卫星运行周期,我们就可以估算出该行星的密度.
典型例题7——万有引力定律的应用
??行星恒星的运动轨道近似是圆形,周期 的平方与轨道半径 的三次方的比为常数,设 ,则 的大小
??A、只跟恒星的质量有关????????B、只跟行星的质量有关
??C、跟行星恒星的质量都有关??????D、跟行星恒星的质量都没关
??解:由万有引力定律得:
??故选A
典型例题8——关于双星的例题
??两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动,现测得两行星中心距离为 ,其周期为 。求两行星的总质量。
??解:由万有引力定律得:
???? ???????????????????
??
??解得:
典型例题9——关于“和平号”空间站的例题
??1986年2月20日发射升空的“和平号”空间站,在服役15年后于2001年3月23日坠落在太平洋.“和平号”风风雨雨15年铸就了辉煌业绩,已成为航天史上的永恒篇章.
??“和平号”空间站总质量137t,工作容积超过400m3.是迄今为止人类探索太空规模最大的航天器,有“人造天宫”之称.在太空运行的这一“庞然大物”按照地面指令准确降落在预定海域,这在人类历史上还是第一次.“和平号”空间站正常运行时,距离地面的平均高度大约是350km.为保证空间站最终安全坠毁,俄罗斯航天局控制中心对空间站的运行做了精心安排和控制.在坠毁前空间站已经顺利进入指定的低空轨道,此时“和平号”距离地面的高度大约为240km.在“和平号”沿指定的低空轨道运行时,其轨道高度平均每昼夜降低2.7km.
??设“和平号”空间站正常运行时沿高度为350km圆形轨道运行,在坠落前沿高度240km的指定圆形低空轨道运行.而且沿指定的低空轨道运行时,每运行一周空间站高度变化很小,因此计算时对空间站的每一周的运动都可以作为匀速圆周运动处理.
??(1)空间站沿正常轨道运行时的加速度与沿指定的低空轨道运行时加速度大小的比值多大?(计算时保留2位有效数字)
??(2)空间站沿指定的低空轨道运行时,每运行一周过程中空间站高度平均变化多大?(计算中取地球半径 ,计算时保留1位有效数字.)
??解:
??(1)根据 , : =0.97
??(2) =2.7km
典型例题10——万有引力与圆周运动公式的综合运用
??用 表示地球通讯卫星(同步卫星)的质量, 表示它离地面的高度, 表示地球的半径, 表示地球表面处的重力加速度, 表示地球自转的角速度,则通讯卫星所受万有引力的大小为:
??A、等于零??????????????????? B、等于
??C、等于 ????????? D、以上结果都不正确
??解:可以认为近地表面地重力近似等于万有引力大小:
?? ,则得到:
??即: ,这样,当通讯卫星在距离地面 高处运行时,其万有引力大小就是:
?? ;选择选项B;
??另外同步卫星与地球自传角速度相等,因此:
?? ;
??解得: ,就得到了选项C.
??因此选择BC.
典型例题11——实际应用题
??2000年1月26日我国发射了一颗同步卫星,其定点位置与东经98°的经线在同一平面内,若把甘肃省嘉峪关处的经度和纬度近似取为东经98°和北纬 ,已知地球半径 、地球自转周期 、地球表面重力加速度 (视为常量)和光速 。试求该同步卫星发出的微波信号传到嘉峪关处的接收站所需的时间(要求用题给的已知量的符号表示)。
??解:设 为卫星质量, 为地球质量, 为卫星到地球中心的距离, 为卫星绕地心转动的角速度,由万有引力定律和牛顿定律有,
?????????????????????????????????????????? ①
??式中 为万有引力恒量,因同步卫星绕地心转动的角速度 与地球自转的角速度相等有:
???????????????????? ???????????②
因
得 ?????????????????????????? ③
??设嘉峪关到同步卫星的距离为 ,如图所示,由余弦定理:
??????????????? ④
??所求时间为:
????????????????????????????????? ⑤
??由以上各式得:
???? ⑥
典型例题12——关于通讯卫星
??我国发射的亚洲一号通讯卫星的质量为m,如果地球半径为R,自转角速度为 ,表面的重力加速度为 ,则亚洲一号( ????)
??A、距地面高度
??B、环绕速度
??C、受到地球引力为
??D、受到地球引力为
??分析:(A)
??∴
??故应选A.
??(B)
??∴ 或
??即
??
??∴ ,故
??∴B正确.
??(C)引力
??∴C正确.
??(D)只有地面附近引力才近似等于 ,现在是高空.
??故D错.
??解:本题正确选项为ABC.
??点评:通讯卫星必须处在地球赤道正上方确定的高度处,且卫星绕地球作匀速圆周运动的周期等于地球自转的周期( h).
典型例题13——关于太阳系质量的运算
??经天文学家观察,太阳在绕着银河系中心(银心)的圆形轨道上运行,这个轨道半径约为3×104光年(约等于2.8×1020m),转动一周的周期约为2亿年(约等于6.3×1015s)太阳作圆周运动的向心力是来自位于它轨道内侧的大量星体的引力,可以把这些星体的全部质量看作集中在银河系中心来处理问题.( =6.67×10-11N·m2/kg2)
??(1)从给出的数据来计算太阳轨道内侧这些星体的总质量.
??(2)试求出太阳在圆周运动轨道上的加速度.
??解:(1)由万有引力定律得:
??解得: =3.3×1041(kg)
??(2) =3.1×10-10m/s2
