北师大版九年级数学下册 第三章 圆达标检测卷(含答案)
文档属性
| 名称 | 北师大版九年级数学下册 第三章 圆达标检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 889.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-03 23:40:56 | ||
图片预览



文档简介
北师大版九年级数学下册 第三章 达标检测卷
(考试时间:120分钟 满分:120分)
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.已知⊙P的半径为4,圆心P的坐标为(1,2),点Q的坐标为(0,5),则点Q与⊙P位置关系是( )
A.点Q在⊙P外 B.点Q在⊙P上
C.点Q在⊙P内 D.不能确定
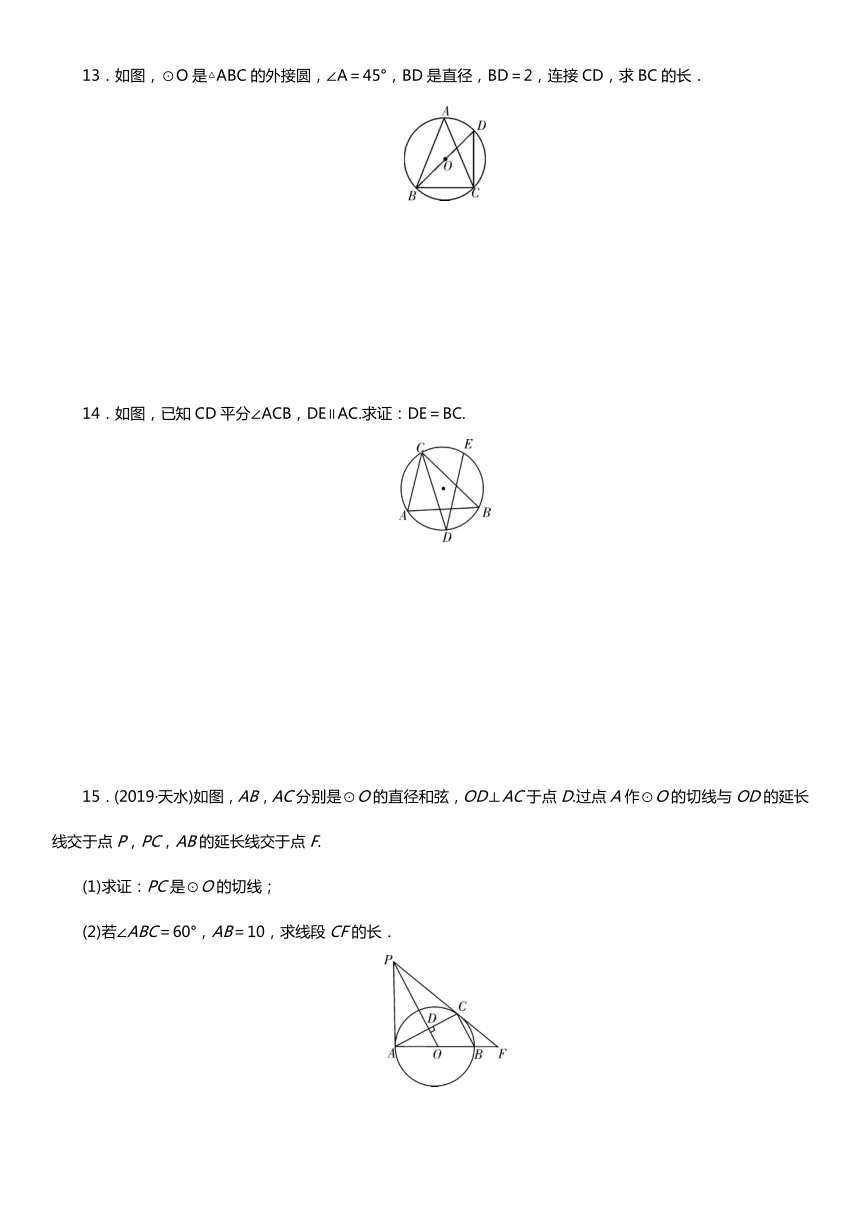
2.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD等于( )
A.20° B.40° C.50° D.80°
3.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( )
A.π B.π C.2π D.3π
4.同一个圆的内接正六边形和外切正六边形的周长之比为( )
A.3∶4 B.∶2 C.2∶ D.1∶2
5.如图,AC是⊙O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8 cm,AE=2 cm,则OF的长度是( )
A.3 cm B. cm C.2.5 cm D. cm
6.如图,将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=,则四边形AB1ED的内切圆半径为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于 .
8.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10 cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
9.如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 度.
10.(2019·内江)如图,在平行四边形ABCD中,AB11.如图,P是反比例函数y=(x>0)的图象上一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=3相切时,点P的坐标为 .
12.(2019·包头)如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为 .
三、(本大题共5小题,每小题6分,共30分)
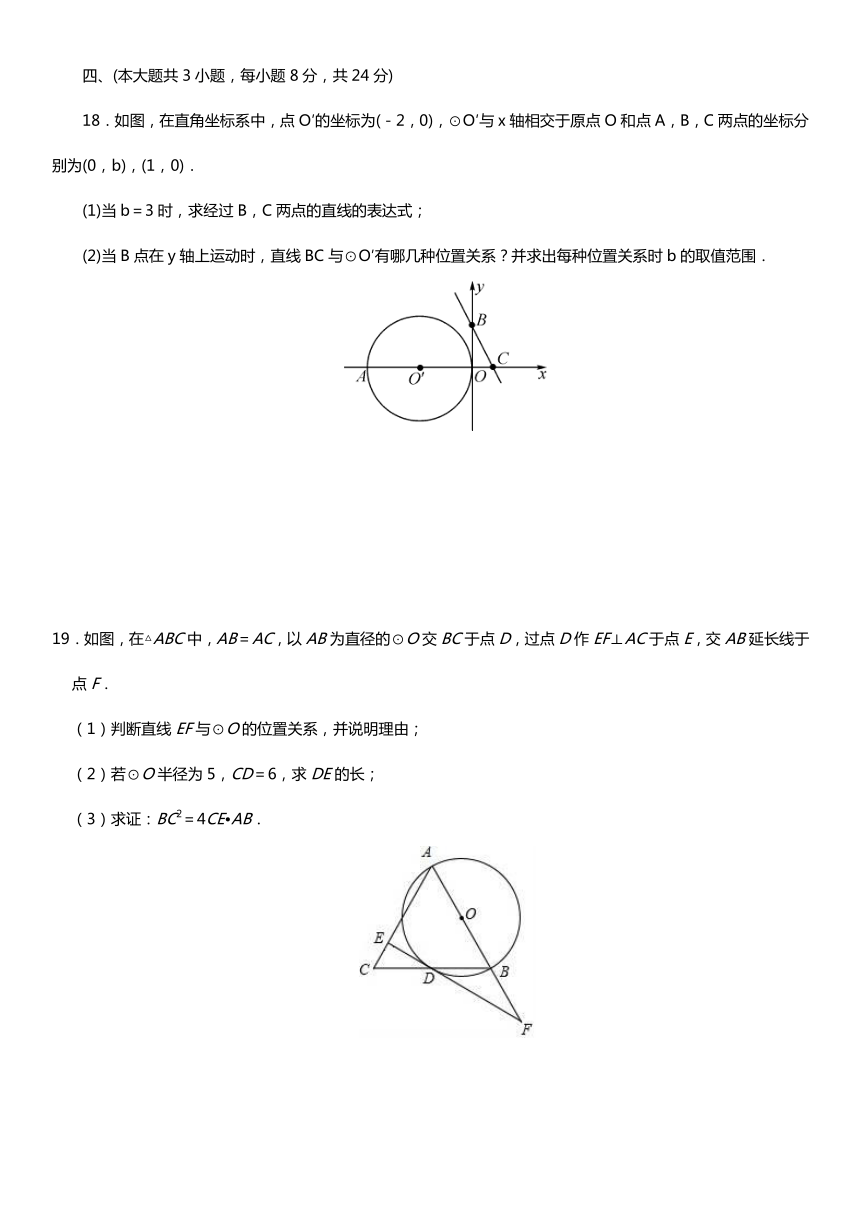
13.如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
14.如图,已知CD平分∠ACB,DE∥AC.求证:DE=BC.
15.(2019·天水)如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC,AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.
16.如图所示,⊙O的直径AB长为6,弦AC的长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.
17.(2019·通辽)如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD ,连接AF.
(1)判断直线AF与⊙O的位置关系,并说明理由.
(2)若AC=10,tan∠CAE=,求AE的长.
四、(本大题共3小题,每小题8分,共24分)
18.如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线的表达式;
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB延长线于点F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为5,CD=6,求DE的长;
(3)求证:BC2=4CE?AB.
20.(齐齐哈尔中考)如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.
五、(本大题共2小题,每小题9分,共18分)
21.(2019·安顺)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:点H为CE的中点;
(3)若BC=10,cos C=,求AE的长.
22.如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若,AD=2,求BC的长;
(3)如图②,在(2)的条件下,连接AE,延长AE和BC,交于点G,求GE的长.
六、(本大题共12分)
23.(2019·荆州)如图AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,在射线l上取点F,使FC=FD.
(1)求证:FC是⊙O的切线;
(2)当点E是的中点时,
①若∠BAC=60°,判断O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
②若tan∠ABC=,且AB=20,求DE的长.
参考答案
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.已知⊙P的半径为4,圆心P的坐标为(1,2),点Q的坐标为(0,5),则点Q与⊙P位置关系是( C )
A.点Q在⊙P外 B.点Q在⊙P上
C.点Q在⊙P内 D.不能确定
2.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD等于( D )
A.20° B.40° C.50° D.80°
3.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( C )
A.π B.π C.2π D.3π
4.同一个圆的内接正六边形和外切正六边形的周长之比为( B )
A.3∶4 B.∶2 C.2∶ D.1∶2
5.如图,AC是⊙O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8 cm,AE=2 cm,则OF的长度是( D )
A.3 cm B. cm C.2.5 cm D. cm
6.如图,将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=,则四边形AB1ED的内切圆半径为( B )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69° .
8.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10 cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
9.如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=115度.
10.(2019·内江)如图,在平行四边形ABCD中,AB11.如图,P是反比例函数y=(x>0)的图象上一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=3相切时,点P的坐标为 (1,4)或(2,2) .
12.(2019·包头)如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为__2__.
三、(本大题共5小题,每小题6分,共30分)
13.如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
解:在⊙O中,∵∠A=45°,∴∠D=45°.
∵BD为⊙O的直径,
∴∠BCD=90°,
∴BC=BD·sin 45°=2×=.
14.如图,已知CD平分∠ACB,DE∥AC.求证:DE=BC.
证明:∵CD平分∠ACB,∴∠ACD=∠BCD,∴=,∵DE∥AC,∴∠ACD=∠CDE,∴=,∴=,∴=,∴DE=BC.
15.(2019·天水)如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC,AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.
(1)证明:连接OC,∵OD⊥AC,OD经过圆心O,∴AD=CD,∴PA=PC,∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP,∵PA是⊙O的切线,∴∠OAP=90°.∴∠OCP=90°,即OC⊥PC∴PC是⊙O的切线.
(2)解:∵OB=OC,∠OBC=60°,∴△OBC是等边三角形,∴∠COB=60°,∵AB=10,∴OC=5,由(1)知∠OCF=90°,∴CF=OC·tan∠COB=5.
16.如图所示,⊙O的直径AB长为6,弦AC的长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.
解:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ABC中,由勾股定理,得
BC===4.
又∵CD平分∠ACB,
∴=,∴AD=BD.
在Rt△ABD中,由勾股定理,得AD=BD=AB=×6=3.
∴S四边形ADBC=S△ABC+S△ABD=4+9,
∴四边形ADBC的面积为4+9.
17.(2019·通辽)如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD ,连接AF.
(1)判断直线AF与⊙O的位置关系,并说明理由.
(2)若AC=10,tan∠CAE=,求AE的长.
解:(1)直线AF是⊙O的切线,理由是:连接AC,∵AB为⊙O直径,∴∠ACB=90°,∴AC⊥BC,∵CF=CD,∴∠CAF=∠EAC,∵AC=CE,∴∠E=∠EAC,∵∠B=∠E,∴∠B=∠FAC,∵∠B+∠BAC=90°,∴∠FAC+∠BAC=90°,∴OA⊥AF,又∵点A在⊙O上,∴直线AF是⊙O的切线.
(2)过点C作CM⊥AE,∵tan∠CAE=,∴=,∵AC=10,∴设CM=3x,则AM=4x,在Rt?ACM中,根据勾股定理,CM2+AM2=AC2,∴(3x)2+(4x)2=100,解得x=2,∴AM=8,∵AC=CE,∴AE=2AM=2×8=16.
四、(本大题共3小题,每小题8分,共24分)
18.如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线的表达式;
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
解:(1)直线BC表达式为y=-3x+3.
(2)当BC切⊙O′于第二象限时,记切点为点D.易得DC=.
∵BO=BD=b,∴BC=-b.
12+b2=(-b)2,得b=.同理当BC切⊙O′于第三象限D1点时,可求得b=-.故当b>或b<-时,直线BC与⊙O′相离;当b=或-时,直线BC与⊙O′相切;当-<b<时,直线BC与⊙O′相交.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB延长线于点F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为5,CD=6,求DE的长;
(3)求证:BC2=4CE?AB.
解:(1)EF与⊙O相切,理由如下:
连接AD,OD,如图所示:
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=BC.
∵OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC.
∵EF⊥AC,
∴EF⊥OD.
∴EF与⊙O相切.
(2)解:由(1)知∠ADC=90°,AC=AB=10,
在Rt△ADC中,由勾股定理得:AD===8.
∵SACD=AD?CD=AC?DE,
∴×8×6=×10×DE.
∴DE=.
(3)证明:由(1)得:CD=BC,AD⊥BC,
∴∠ADC=90°,
∵EF⊥AC,
∴∠DEC=90°=∠ADC,
∵∠C=∠C,
∴△CDE∽△CAD,
∴=,
∴CD2=CE?AB,
∵AB=AC,
∴BC2=CE?AB,
∴BC2=4CE?AB.
20.(齐齐哈尔中考)如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°.
又∵∠A=∠DEB,
∠DEB=∠DBC,
∴∠A=∠DBC,
∴∠DBC+∠ABD=90°,即∠ABC=90°
∴BC是⊙O的切线.
(2)解:∵BF=BC=2且∠ADB=90°,
∴∠CBD=∠FBD,
又∵OE∥BD,∴∠FBD=∠OEB.
∵OE=OB,∴∠OEB=∠OBE,
∴∠CBD=∠DBE=∠OBE=∠ABC=×90°=30°,
∴∠C=60°,∴AB=BC=2,
∴⊙O的半径为,连接OD,
∴阴影部分面积为S扇形OBD- S△OBD=π×3-×3=-.
五、(本大题共2小题,每小题9分,共18分)
21.(2019·安顺)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:点H为CE的中点;
(3)若BC=10,cos C=,求AE的长.
(1)解:DH与⊙O相切.理由:连接OD,AD,∵AB为直径,∴∠ADB=90°, ∵AB=AC,∴BD=CD,∵OA=OB,∴OD∥AC,∵DH⊥AC,∴DH⊥OD,∴DH为⊙O的切线.
(2)证明:连接DE,∵A,B,D,E四点共圆,∴∠DEC=∠B,∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴CD=ED,∵DH⊥CE,∴点H为CE的中点.
(3)解:CD=BC=5,∵cos C==,∴AC=5,∵cos C==,∴CH=,∴CE=2CH=2,∴AE=AC-CE=3.
22.如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若,AD=2,求BC的长;
(3)如图②,在(2)的条件下,连接AE,延长AE和BC,交于点G,求GE的长.
解:(1)证明:如图①,连接OE、OC,
∵DE与⊙O相切于点E,
∴∠OEC=90°,
在△OBC和△OEC中,
,
∴△OBC≌△OEC(SSS)
∴∠OBC=∠OEC=90°,
∴BC为⊙O的切线;
(2)作DF⊥BC于F,
则四边形ABFD为矩形,
∴BF=AD=2,DF=,
由切线长定理得,DE=AD=2,
设BC=x,则CE=x,CF=x﹣2,CD=x+2,
在Rt△DFC中,CD2=DF2+FC2,即(x+2)2=(2)2+(x﹣2)2,
解得,x=,即BC=;
(3)如图②,连接BE,作DF⊥BC于F,
∵AD∥BG,
∴∠DAE=∠EGC,
∵DA=DE,
∴∠DAE=∠AED,
∵∠AED=∠CEG,
∴∠EGC=∠CEG,
∴CG=CE=CB=,
∴BG=5,
∴AG===3,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠GEB=∠GBA,又∠G=∠G,
∴△GEB∽△GBA,
∴=,
∴BG2=GE?GA,
∴GE===.
六、(本大题共12分)
23.(2019·荆州)如图AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,在射线l上取点F,使FC=FD.
(1)求证:FC是⊙O的切线;
(2)当点E是的中点时,
①若∠BAC=60°,判断O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
②若tan∠ABC=,且AB=20,求DE的长.
(1)证明:连接OC,∵OB=OC,∴∠OBC=∠OCB,∵PF⊥AB,∴∠BPD=90°,∴∠OBC+∠BDP=90°,∵FC=FD, ∴∠FCD=∠FDC,∵∠FDC=∠BDP,∴∠FCD=∠BDP,∴∠OCB+∠FCD=90°,∴OC⊥FC,FC是⊙O的切线.
(2)解:连接OC,OE,BE,CE,OE与BC交于H.
①以O,B,E,C为顶点的四边形是菱形.理由:∵AB是直径,∴∠ACB=90°,∵∠BAC=60°,∴∠BOC=120°,∵点E是的中点,∴∠BOE=∠COE=60°,∵OB=OE=OC,∴△BOE,△COE均为等边三角形,∴OB=BE=CE=OC,
∴四边形BOCE是菱形.②∵=tan∠ABC=,设AC=3k,BC=4k,k>0.由AC2+BC2=AB2,即(3k)2+(4k)2=202,解得k=4,∴AC=12,BC=16,∵点E是的中心,∴OE⊥BC,BH=CH=8,∵S△BOE=OE·BH=OB·PE,即×10×8=×10×PE,∴PE=8,又OP==6,∴BP=OB-OP=4,∵=tan∠ABC=,
∴DP=BP=3,∴DE=PE-DP=8-3=5.
(考试时间:120分钟 满分:120分)
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.已知⊙P的半径为4,圆心P的坐标为(1,2),点Q的坐标为(0,5),则点Q与⊙P位置关系是( )
A.点Q在⊙P外 B.点Q在⊙P上
C.点Q在⊙P内 D.不能确定
2.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD等于( )
A.20° B.40° C.50° D.80°
3.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( )
A.π B.π C.2π D.3π
4.同一个圆的内接正六边形和外切正六边形的周长之比为( )
A.3∶4 B.∶2 C.2∶ D.1∶2
5.如图,AC是⊙O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8 cm,AE=2 cm,则OF的长度是( )
A.3 cm B. cm C.2.5 cm D. cm
6.如图,将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=,则四边形AB1ED的内切圆半径为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于 .
8.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10 cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
9.如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 度.
10.(2019·内江)如图,在平行四边形ABCD中,AB
12.(2019·包头)如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为 .
三、(本大题共5小题,每小题6分,共30分)
13.如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
14.如图,已知CD平分∠ACB,DE∥AC.求证:DE=BC.
15.(2019·天水)如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC,AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.
16.如图所示,⊙O的直径AB长为6,弦AC的长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.
17.(2019·通辽)如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD ,连接AF.
(1)判断直线AF与⊙O的位置关系,并说明理由.
(2)若AC=10,tan∠CAE=,求AE的长.
四、(本大题共3小题,每小题8分,共24分)
18.如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线的表达式;
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB延长线于点F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为5,CD=6,求DE的长;
(3)求证:BC2=4CE?AB.
20.(齐齐哈尔中考)如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.
五、(本大题共2小题,每小题9分,共18分)
21.(2019·安顺)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:点H为CE的中点;
(3)若BC=10,cos C=,求AE的长.
22.如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若,AD=2,求BC的长;
(3)如图②,在(2)的条件下,连接AE,延长AE和BC,交于点G,求GE的长.
六、(本大题共12分)
23.(2019·荆州)如图AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,在射线l上取点F,使FC=FD.
(1)求证:FC是⊙O的切线;
(2)当点E是的中点时,
①若∠BAC=60°,判断O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
②若tan∠ABC=,且AB=20,求DE的长.
参考答案
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.已知⊙P的半径为4,圆心P的坐标为(1,2),点Q的坐标为(0,5),则点Q与⊙P位置关系是( C )
A.点Q在⊙P外 B.点Q在⊙P上
C.点Q在⊙P内 D.不能确定
2.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD等于( D )
A.20° B.40° C.50° D.80°
3.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( C )
A.π B.π C.2π D.3π
4.同一个圆的内接正六边形和外切正六边形的周长之比为( B )
A.3∶4 B.∶2 C.2∶ D.1∶2
5.如图,AC是⊙O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8 cm,AE=2 cm,则OF的长度是( D )
A.3 cm B. cm C.2.5 cm D. cm
6.如图,将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=,则四边形AB1ED的内切圆半径为( B )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69° .
8.如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10 cm,点D在量角器上的读数为60°,则该直尺的宽度为 cm.
9.如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=115度.
10.(2019·内江)如图,在平行四边形ABCD中,AB
12.(2019·包头)如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为__2__.
三、(本大题共5小题,每小题6分,共30分)
13.如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,BD=2,连接CD,求BC的长.
解:在⊙O中,∵∠A=45°,∴∠D=45°.
∵BD为⊙O的直径,
∴∠BCD=90°,
∴BC=BD·sin 45°=2×=.
14.如图,已知CD平分∠ACB,DE∥AC.求证:DE=BC.
证明:∵CD平分∠ACB,∴∠ACD=∠BCD,∴=,∵DE∥AC,∴∠ACD=∠CDE,∴=,∴=,∴=,∴DE=BC.
15.(2019·天水)如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC,AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.
(1)证明:连接OC,∵OD⊥AC,OD经过圆心O,∴AD=CD,∴PA=PC,∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP,∵PA是⊙O的切线,∴∠OAP=90°.∴∠OCP=90°,即OC⊥PC∴PC是⊙O的切线.
(2)解:∵OB=OC,∠OBC=60°,∴△OBC是等边三角形,∴∠COB=60°,∵AB=10,∴OC=5,由(1)知∠OCF=90°,∴CF=OC·tan∠COB=5.
16.如图所示,⊙O的直径AB长为6,弦AC的长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.
解:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ABC中,由勾股定理,得
BC===4.
又∵CD平分∠ACB,
∴=,∴AD=BD.
在Rt△ABD中,由勾股定理,得AD=BD=AB=×6=3.
∴S四边形ADBC=S△ABC+S△ABD=4+9,
∴四边形ADBC的面积为4+9.
17.(2019·通辽)如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD ,连接AF.
(1)判断直线AF与⊙O的位置关系,并说明理由.
(2)若AC=10,tan∠CAE=,求AE的长.
解:(1)直线AF是⊙O的切线,理由是:连接AC,∵AB为⊙O直径,∴∠ACB=90°,∴AC⊥BC,∵CF=CD,∴∠CAF=∠EAC,∵AC=CE,∴∠E=∠EAC,∵∠B=∠E,∴∠B=∠FAC,∵∠B+∠BAC=90°,∴∠FAC+∠BAC=90°,∴OA⊥AF,又∵点A在⊙O上,∴直线AF是⊙O的切线.
(2)过点C作CM⊥AE,∵tan∠CAE=,∴=,∵AC=10,∴设CM=3x,则AM=4x,在Rt?ACM中,根据勾股定理,CM2+AM2=AC2,∴(3x)2+(4x)2=100,解得x=2,∴AM=8,∵AC=CE,∴AE=2AM=2×8=16.
四、(本大题共3小题,每小题8分,共24分)
18.如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线的表达式;
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
解:(1)直线BC表达式为y=-3x+3.
(2)当BC切⊙O′于第二象限时,记切点为点D.易得DC=.
∵BO=BD=b,∴BC=-b.
12+b2=(-b)2,得b=.同理当BC切⊙O′于第三象限D1点时,可求得b=-.故当b>或b<-时,直线BC与⊙O′相离;当b=或-时,直线BC与⊙O′相切;当-<b<时,直线BC与⊙O′相交.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB延长线于点F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为5,CD=6,求DE的长;
(3)求证:BC2=4CE?AB.
解:(1)EF与⊙O相切,理由如下:
连接AD,OD,如图所示:
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=BC.
∵OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC.
∵EF⊥AC,
∴EF⊥OD.
∴EF与⊙O相切.
(2)解:由(1)知∠ADC=90°,AC=AB=10,
在Rt△ADC中,由勾股定理得:AD===8.
∵SACD=AD?CD=AC?DE,
∴×8×6=×10×DE.
∴DE=.
(3)证明:由(1)得:CD=BC,AD⊥BC,
∴∠ADC=90°,
∵EF⊥AC,
∴∠DEC=90°=∠ADC,
∵∠C=∠C,
∴△CDE∽△CAD,
∴=,
∴CD2=CE?AB,
∵AB=AC,
∴BC2=CE?AB,
∴BC2=4CE?AB.
20.(齐齐哈尔中考)如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°.
又∵∠A=∠DEB,
∠DEB=∠DBC,
∴∠A=∠DBC,
∴∠DBC+∠ABD=90°,即∠ABC=90°
∴BC是⊙O的切线.
(2)解:∵BF=BC=2且∠ADB=90°,
∴∠CBD=∠FBD,
又∵OE∥BD,∴∠FBD=∠OEB.
∵OE=OB,∴∠OEB=∠OBE,
∴∠CBD=∠DBE=∠OBE=∠ABC=×90°=30°,
∴∠C=60°,∴AB=BC=2,
∴⊙O的半径为,连接OD,
∴阴影部分面积为S扇形OBD- S△OBD=π×3-×3=-.
五、(本大题共2小题,每小题9分,共18分)
21.(2019·安顺)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:点H为CE的中点;
(3)若BC=10,cos C=,求AE的长.
(1)解:DH与⊙O相切.理由:连接OD,AD,∵AB为直径,∴∠ADB=90°, ∵AB=AC,∴BD=CD,∵OA=OB,∴OD∥AC,∵DH⊥AC,∴DH⊥OD,∴DH为⊙O的切线.
(2)证明:连接DE,∵A,B,D,E四点共圆,∴∠DEC=∠B,∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∴CD=ED,∵DH⊥CE,∴点H为CE的中点.
(3)解:CD=BC=5,∵cos C==,∴AC=5,∵cos C==,∴CH=,∴CE=2CH=2,∴AE=AC-CE=3.
22.如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若,AD=2,求BC的长;
(3)如图②,在(2)的条件下,连接AE,延长AE和BC,交于点G,求GE的长.
解:(1)证明:如图①,连接OE、OC,
∵DE与⊙O相切于点E,
∴∠OEC=90°,
在△OBC和△OEC中,
,
∴△OBC≌△OEC(SSS)
∴∠OBC=∠OEC=90°,
∴BC为⊙O的切线;
(2)作DF⊥BC于F,
则四边形ABFD为矩形,
∴BF=AD=2,DF=,
由切线长定理得,DE=AD=2,
设BC=x,则CE=x,CF=x﹣2,CD=x+2,
在Rt△DFC中,CD2=DF2+FC2,即(x+2)2=(2)2+(x﹣2)2,
解得,x=,即BC=;
(3)如图②,连接BE,作DF⊥BC于F,
∵AD∥BG,
∴∠DAE=∠EGC,
∵DA=DE,
∴∠DAE=∠AED,
∵∠AED=∠CEG,
∴∠EGC=∠CEG,
∴CG=CE=CB=,
∴BG=5,
∴AG===3,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠GEB=∠GBA,又∠G=∠G,
∴△GEB∽△GBA,
∴=,
∴BG2=GE?GA,
∴GE===.
六、(本大题共12分)
23.(2019·荆州)如图AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,在射线l上取点F,使FC=FD.
(1)求证:FC是⊙O的切线;
(2)当点E是的中点时,
①若∠BAC=60°,判断O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
②若tan∠ABC=,且AB=20,求DE的长.
(1)证明:连接OC,∵OB=OC,∴∠OBC=∠OCB,∵PF⊥AB,∴∠BPD=90°,∴∠OBC+∠BDP=90°,∵FC=FD, ∴∠FCD=∠FDC,∵∠FDC=∠BDP,∴∠FCD=∠BDP,∴∠OCB+∠FCD=90°,∴OC⊥FC,FC是⊙O的切线.
(2)解:连接OC,OE,BE,CE,OE与BC交于H.
①以O,B,E,C为顶点的四边形是菱形.理由:∵AB是直径,∴∠ACB=90°,∵∠BAC=60°,∴∠BOC=120°,∵点E是的中点,∴∠BOE=∠COE=60°,∵OB=OE=OC,∴△BOE,△COE均为等边三角形,∴OB=BE=CE=OC,
∴四边形BOCE是菱形.②∵=tan∠ABC=,设AC=3k,BC=4k,k>0.由AC2+BC2=AB2,即(3k)2+(4k)2=202,解得k=4,∴AC=12,BC=16,∵点E是的中心,∴OE⊥BC,BH=CH=8,∵S△BOE=OE·BH=OB·PE,即×10×8=×10×PE,∴PE=8,又OP==6,∴BP=OB-OP=4,∵=tan∠ABC=,
∴DP=BP=3,∴DE=PE-DP=8-3=5.
