2019-2020学年北师大版九年级数学上册第四章:图形的相似复习学案(无答案)
文档属性
| 名称 | 2019-2020学年北师大版九年级数学上册第四章:图形的相似复习学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 456.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览




文档简介
2019秋北师大版九年级数学上册第四章图形的相似复习学案
知识回顾与例题讲解
1、线段的比与成比例线段
? 相关定义:
? 线段的比:如果选用同一个长度单位量得两条线段,的长度分别是,,那么就说这两条线段的比,或者写成。其中,线段,分别叫做这个线段比的前项和后项。如果把表示成比值,那么,或
? 比例线段:四条线段,,,中,如果与的比等于与的比,即,那么这四条线段,,,叫做成比例线段,简称比例线段
? 比例线段性质:
? 如果,那么
? 如果(,,,都不等于0),那么
? 如果,那么
? 如果,那么
? 例题:
(1) 若∶3 =∶4 =∶5 , 且, 则;
(2) 已知∶∶= 3∶4∶5 , 且, 那么;
(3)若, 则;
(4) 已知∶4 =∶5 = z∶6 , 则 ①∶∶z = , ② ∶;
2、黄金分割
? 定义:如下图所示,设点是线段上一点,点把线段分成两条线段和,若,妈妈称线段被点黄金分割,点叫做线段的黄金分割点,与叫做黄金比
? 例题
(1)美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女士身高165cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
A.4cm B.6cm C.8cm D.10cm
(2)如图是一种贝壳的俯视图,点分线段近似于黄金分割.已知=10cm,则的长约为 cm.(结果精确到0.1cm)
3、相似多边形
? 相似多边形:各角对应相等、各边对应成比例的两个多边形叫做相似多边形
? 相似比:相似多边形对应边的比叫做相似比
4、相似三角形
? 定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。与相似,记作
? 两个三角形相似与否的判定定理
? 两角对应相等的两个三角形相似
? 三边对应成比例的两个三角形相似
? 两边对应成比例且夹角相等的两个三角形相似
? 例题:
(1) 三角尺在灯泡的照射下在墙上形成影子(如图4所示).现测得,这个三角尺的周长与它在墙上形成的影子的周长的比是 .
(2) 如图8所示,给出下列条件:
①;②;
③; ④.
其中单独能够判定的个数为( )
A.1 B.2 C.3 D.4
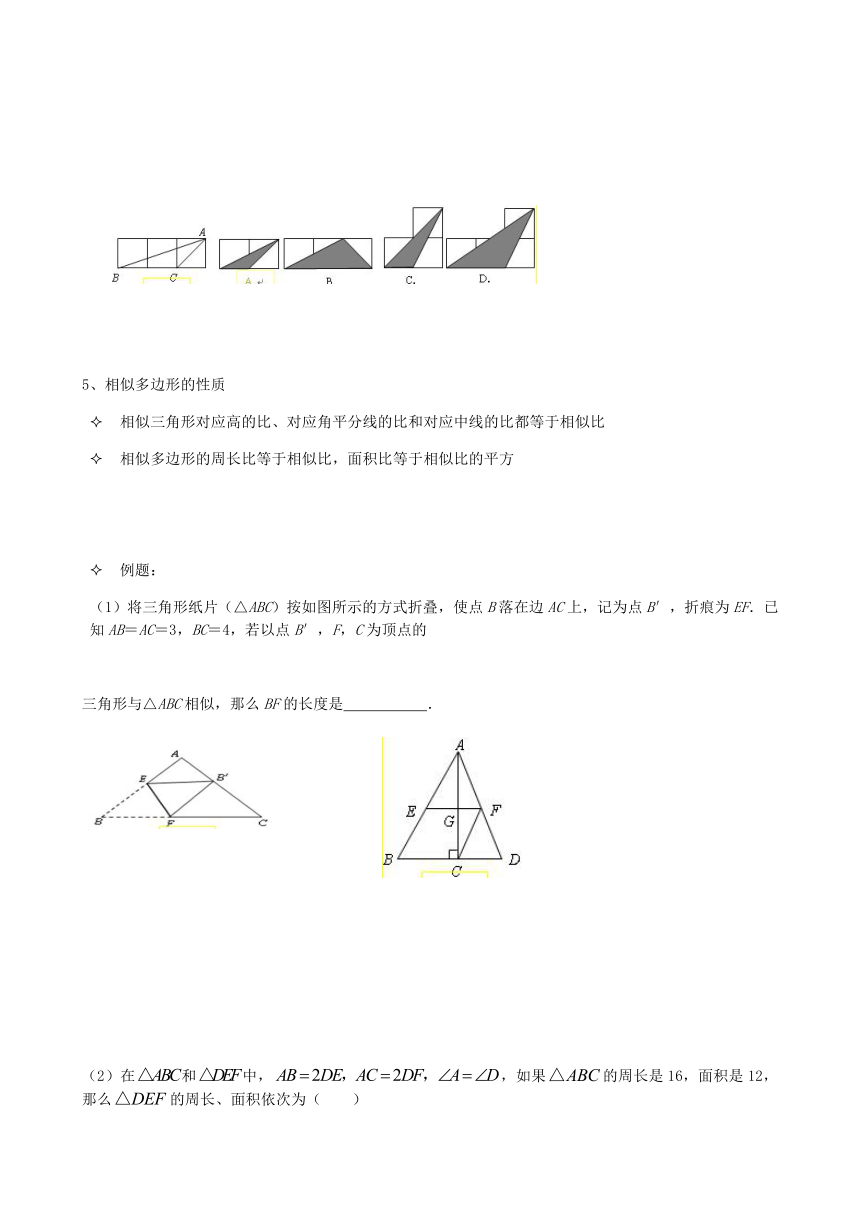
(3) 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是( )
5、相似多边形的性质
? 相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比
? 相似多边形的周长比等于相似比,面积比等于相似比的平方
? 例题:
(1)将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的
三角形与△ABC相似,那么BF的长度是 .
(2)在和中,,如果的周长是16,面积是12,那么的周长、面积依次为( )
A.8,3 B.8,6 C.4,3 D.4,6
(3)如图,中,直线交于点交于点交于点若则 .
6、图形的放大与缩小
? 定义:如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点,那么这两个图形叫做位似图形,这个点叫做位似中心,这是的相似比又称为位似比。
? 位似图形性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比
课堂演练:
1.若△ABC∽△DEF, △ABC与△DEF的相似比为1∶2,则△ABC与△DEF的周长比为( )
A.1∶4 B.1∶2 C.2∶1 D.1∶
2.如图, 中,于一定能确定为直角三角形的条件的个数是( )
①②③
④⑤
A.1 B.2 C.3 D.4
3.已知与相似且面积比为4∶25,则与的相似比为 .
4.两个相似三角形的周长比为,则面积比为 ( )
(A) (B) (C) (D
5.如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
①∠AFC=∠C; ②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
其中正确的结论是 (填写所有正确结论的序号).
6.如上图,已知零件的外径为25mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10mm,则零件的厚度x= mm.
7.如图,在△ABC中,已知DE∥BC,
AD=4,DB=8,DE=3,
(1)求的值;
(2)求BC的长.
8.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.
9.小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).
已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
10 .E 为正方形 ABCD 的边上的中点,AB = 1 ,MN⊥DE 交 AB 于 M,交 DC 的延长线于 N,求证:⑴ EC= DC·CN; ⑵ CN = ; ⑶ NE = ;
11.已知,如图,梯形 ABCD 中,AB∥DC,梯形外一点 P,连结 PA、PB 分别交DC 于 F、G,且 DF = FG,对角线 BD 交 AF 于 E,求证:AP∶PF = AE∶EF
12、如图,Rt△ABAC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=( )
A. B. C. D.
13、如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为( )
A、 B、 1 C、 D、
14、如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.
求证:(1);
(2)
15、如图下左,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若?ABC固定不动,?AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以?ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图下右).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD+CE=DE.
(4)在旋转过程中,(3)中的等量关系BD+CE=DE是否始终成立,若成立,请证明,若不成立,请说明理由.
16、如图,四边形和四边形都是平行四边形,点为的中点,分别交于点.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求.
17、如图,在△ABC中,BC>AC, 点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
课后作业
一、
1.在比例尺为1∶50 0000的福建省地图上,量得省会福州到漳州的距离为46厘米,则福州到漳州实际距离约为 千米.
2.若线段,,,成比例,其中,,,则 .
3.已知,则的值为 .
4.两个相似三角形面积比是9∶25,其中一个三角形的周长为36cm,则另一个三角形的周长是 .
5.把一个矩形的各边都扩大4倍,则对角线扩大到 倍,其面积扩大到 倍.
6.厨房角柜的台面是三角形(如图1),如果把各边中点连线所围成三角形铺成黑色大理石,其余部分铺成白色大理石,则黑色大理石的面积与白色大理石的面积之比为 .
8.在同一时刻,高为1.5m的标杆的影长为2.5m,一古塔在地面上影长为50m,那么古塔的高为 .
9.如图3,中,,,,,则 .
10.如图4,在和中,,与的周长之差为10cm,则的周长是 .
二、
1.在下列说法中,正确的是( )
A.两个钝角三角形一定相似
B.两个等腰三角形一定相似
C.两个直角三角形一定相似
D.两个等边三角形一定相似
2.如图5,在中,,分别是、边上的点,,,,则( )
A.60° B.45° C.30° D.20°
3.如果三角形的每条边都扩大为原来的5倍,那么三角形的每个角( )
A.都扩大为原来的5倍
B.都扩大为原来的10倍
C.都扩大为原来的25倍
D.都与原来相等
4.如图6, 在中,,于,若,,则( )
A.2 B.4 C.2 D.3
5.如图7,,,分别是线段和线段的中点,那么线段的长是( )
A.6 B.5 C.4.5 D.3
6.如图8,点是的边延长线上的一点,与相交于点,是的对角线,则图中相似三角形共有( )
A.2对 B.3对 C.4对 D.5对
7.如图9,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
8.如图10,梯形的对角线交于点,有以下四个结论:
①; ②;
③;④.
其中始终正确的有( )
A. 1个 B.2个 C.3个 D.4个
9.如图12,梯形中,,,为上一点,且. 若,,BE∶EC=1∶2,求AB的长.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
