六年级上册数学单元测试-5.图形的变换和位置的确定 西师大版 (含答案)
文档属性
| 名称 | 六年级上册数学单元测试-5.图形的变换和位置的确定 西师大版 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 77.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 00:00:00 | ||
图片预览



文档简介
六年级上册数学单元测试-5.图形的变换和位置的确定
一、单选题
1.东北方也叫作(?? )
A.?北偏东???????????????????????????????????????B.?东偏北???????????????????????????????????????C.?北东
2.把边长3厘米的正方形,按2:1的比放大,放大后的面积是(? )平方厘米.
A.?6?????????????????????????????????????????????B.?12?????????????????????????????????????????????C.?36
3.把线段比例尺 改写成数值比例尺是(? )
A.?1:50????????????????????????????B.?1:100????????????????????????????C.?1:5000000????????????????????????????D.?1:5000
4.在比例尺是1:8的图纸上,甲、乙两个圆的直径比是2:3,那么甲、乙两个圆的实际的直径比是( )
A.?1:8????????????????????????????????????B.?4:9????????????????????????????????????C.?2:3????????????????????????????????????D.?1:4
二、判断题
5.小法官,巧判断.
如果你去商店时,向北走了400米,回来时你应该向东走400米.
6.一个平行四边形的底为15cm,高为5.5cm,如果图形按3:1扩大,那么扩大后的图形面积是247.5cm2 . ( ??)
7.一个图形放大或缩小后,大小发生了变化,形状没变。
8.判断对错. 一个图形按1∶10缩小就是把这个图形的面积缩小为原来的 .
三、填空题
9.钓鱼岛及其附属岛屿自古就是中国的领土,钓鱼岛距温岭市松门镇约390千米。在一幅地图上量出是3厘米,这幅地图的比例尺是________。
10.把地面150千米的距离用5厘米的线段画在地图上,那么,这幅地图的比例尺是________.
11.一幅地图的比例尺是1:5000000,这是________比例尺,图上1厘米表示实际距离________千米.在这地图上量得A、B两地距离是6厘米,实际距离是________千米.
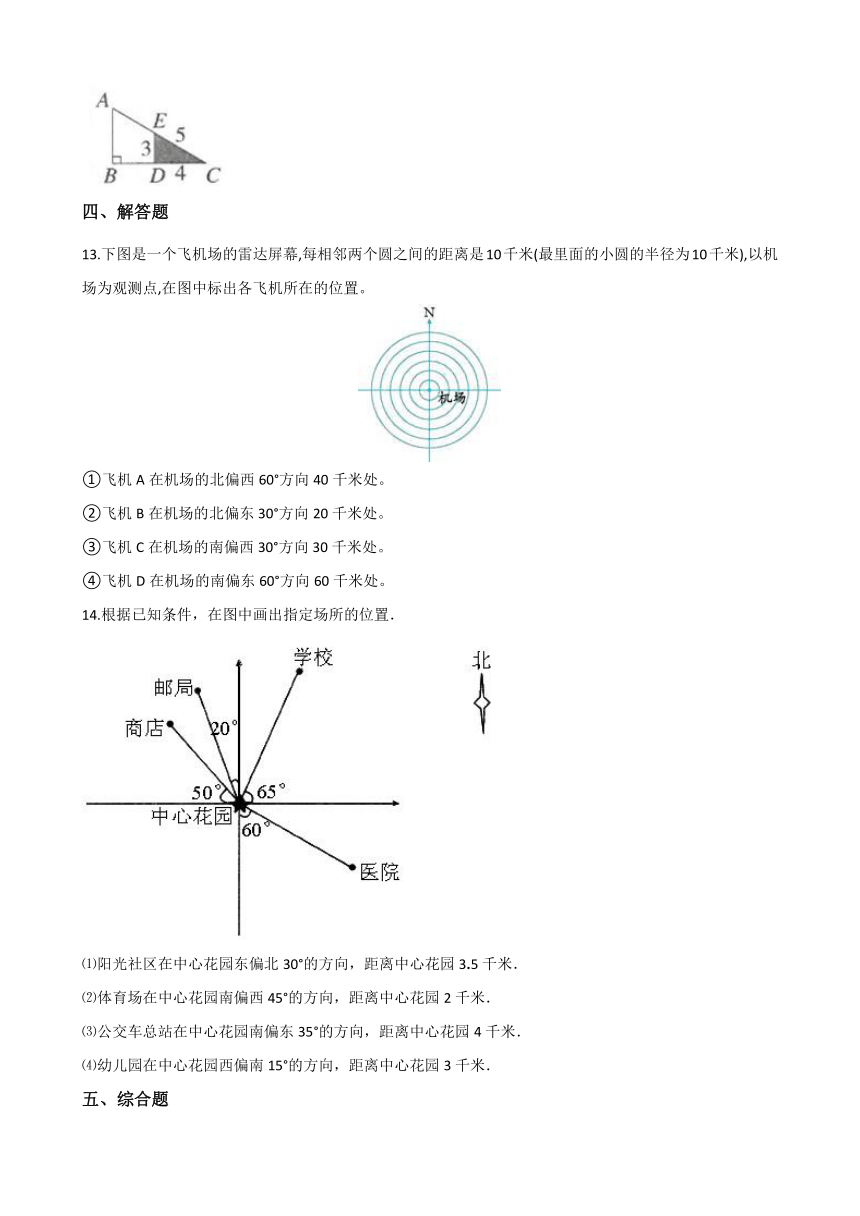
12.如下图,将△EDC放大一定比例成△ABC,直角△DCE的三条边分别是3cm、4cm、5cm。如果AB=6cm,那么AE=________cm。
四、解答题
13.下图是一个飞机场的雷达屏幕,每相邻两个圆之间的距离是10千米(最里面的小圆的半径为10千米),以机场为观测点,在图中标出各飞机所在的位置。
①飞机A在机场的北偏西60°方向40千米处。
②飞机B在机场的北偏东30°方向20千米处。
③飞机C在机场的南偏西30°方向30千米处。
④飞机D在机场的南偏东60°方向60千米处。
14.根据已知条件,在图中画出指定场所的位置. ⑴阳光社区在中心花园东偏北30°的方向,距离中心花园3.5千米. ⑵体育场在中心花园南偏西45°的方向,距离中心花园2千米. ⑶公交车总站在中心花园南偏东35°的方向,距离中心花园4千米. ⑷幼儿园在中心花园西偏南15°的方向,距离中心花园3千米.
五、综合题
15.看图填空
(1)教学楼在操场的________,图书室在操场的________,大门在操场的________,体育馆在操场的________.
(2)图书馆在教学楼的________,体育馆在教学楼的________
六、应用题
16.小东家到学校的实际距离约300米,在地图上的距离是1.5厘米,这幅地图的比例尺是多少?这幅地图上小东家到少年宫的图上距离是2.5厘米,实际距离是多少米?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】东北方也叫作北偏东
【分析】考察了学生根据方向和距离确定物体位置的能力
2.【答案】 C
【解析】【解答】解:3×2=6(厘米)
6×6=36(平方厘米)
答:放大后的正方形的面积是36平方厘米.
故选:C.
【分析】把边长3厘米的正方形按2:1放大后,边长是3×2=6厘米,再利用正方形的面积公式即可解答.本题根据放大与缩小的方法,得出放大后的正方形的边长是解决本题的关键.
3.【答案】C
【解析】【解答】解因为50千米=5000000厘米,
则1厘米:5000000厘米=1:5000000;
【分析】因为图上距离1厘米表示实际距离50千米,化成同一单位后,再据比例尺的意义,即可得解。
故选:C
4.【答案】 C
【解析】【解答】解:令甲乙两圆的图上直径为2d,3d,
根据比例尺可得实际甲乙两圆的直径分别是2d×8=16d,3d×8=24d,
16d:24d=2:3.
故选:C.
【分析】根据比例尺的意义,令甲乙两圆的图上直径为2d,3d,根据比例尺可得实际圆的直径分别是16d,24d,由此利用比例尺进行计算,即可选择正确答案.
二、判断题
5.【答案】 错误
【解析】
6.【答案】 错误
【解析】【解答】(15×3)×(5.5×3) =45×16.5 =742.5(cm2) 原题说法错误。 故答案为:错误。 【分析】根据题意可知,先求出扩大后的平行四边形的底与高,然后用扩大后的底×高=扩大后的平行四边形面积,据此列式解答。
7.【答案】 错误
【解析】【解答】解:如果一个图形的每一部分不是按照一定的比例放大或缩小,那么这个图形不光大小会发生变化,形状也会发生变化。 故答案为:错误。 【分析】把一个图形按一定的比例放大或缩小后,大小发生了变化,形状没变。
8.【答案】错误
【解析】【解答】解:设原正方形边长是1厘米,面积是1×1=1平方厘米; 一个正方形按1:10缩小后,正方形边长是1×(1:10)=1×=厘米,正方形面积=×=平方厘米; ÷1=,所以面积缩小为原来的;所以一个图形按1:10缩小就是把这个图形的面积缩小为原来的说法错误。 故答案为:错误。 【分析】本题先设原正方形边长是1厘米,求出原正方形面积,再根据图上距离=实际距离×比例尺,求出按1:10缩小后,正方形边长和面积是多少,然后进行比较面积的变化,即可解答此题。
三、填空题
9.【答案】1:13000000
【解析】【解答】解:390千米=39000000厘米,比例尺:3:39000000=1:13000000. 故答案为:1:13000000 【分析】先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可求出比例尺.
10.【答案】1:3000000
【解析】【解答】解:150千米=15000000厘米 5:15000000=1:3000000 答:这幅地图的比例尺是1:3000000. 故答案为:1:3000000. 【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比.
11.【答案】数值;50;300
【解析】【解答】解:(1)比例尺是1:5000000,这是数值比例尺,图上1厘米表示实际距离5000000厘米,即50千米;(2)6÷ =30000000(厘米)=300(千米); 故答案为:数值,50,300. 【分析】(1)比例尺是1:5000000,这是数值比例尺,图上1厘米表示实际距离5000000厘米,即50千米;(2)图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出A、B两地之间的实际距离.此题主要考查比例尺的意义以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算.
12.【答案】 5
【解析】【解答】6÷3=2, 5×2-5 =10-5 =5(cm). 故答案为:5. 【分析】观察图可知,△EDC中的直角边ED=3cm,放大后变成了AB,AB=6cm,则放大的比例是6:3=2:1;则放大后斜边AC的长度是:5×2=10cm,AE=AC-EC=10-5=5cm,据此解答. ?
四、解答题
13.【答案】 解:
【解析】【解答】根据分析,作图如下:
【分析】根据图可知,图中是按“上北下南,左西右东”来规定方向的,根据条件“ 每相邻两个圆之间的距离是10千米(最里面的小圆的半径为10千米) ”,以机场为观测点,依据各飞机在机场的方位和距离作图即可.
14.【答案】解:
【解析】【解答】根据分析,作图如下: 【分析】解答此题应该先确定比例尺,根据图意,可以用图上1厘米表示实际1千米,根据方向和距离的描述作图即可.
五、综合题
15.【答案】(1)北面;东面;南面;西面 (2)东南;西南
【解析】【解答】解:(1)教学楼在操场的 北面,图书室在操场的 东面,大门在操场的 南面,体育馆在操场的 西面.(2)图书馆在教学楼的 东南,体育馆在教学楼的 西南;
故答案为:北面,东面,南面,西面,东南,西南.
【分析】平面图中的方向标是:上北、下南、左西、右东,由此即可确定上图中的物体的位置.
六、应用题
16.【答案】解:因为300米=30000厘米, 则1.5厘米:30000厘米=1:20000; 答:这幅地图的比例尺是1:20000; 2.5÷ =50000(厘米), 50000厘米=500米; 答:实际距离是500米.
【解析】【分析】(1)图上距离和实际距离已知,依据“比例尺= ,代入数值,即可求得这幅图的比例尺;(2)求小东家到少年宫的实际距离,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可.解答此题应根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论.
一、单选题
1.东北方也叫作(?? )
A.?北偏东???????????????????????????????????????B.?东偏北???????????????????????????????????????C.?北东
2.把边长3厘米的正方形,按2:1的比放大,放大后的面积是(? )平方厘米.
A.?6?????????????????????????????????????????????B.?12?????????????????????????????????????????????C.?36
3.把线段比例尺 改写成数值比例尺是(? )
A.?1:50????????????????????????????B.?1:100????????????????????????????C.?1:5000000????????????????????????????D.?1:5000
4.在比例尺是1:8的图纸上,甲、乙两个圆的直径比是2:3,那么甲、乙两个圆的实际的直径比是( )
A.?1:8????????????????????????????????????B.?4:9????????????????????????????????????C.?2:3????????????????????????????????????D.?1:4
二、判断题
5.小法官,巧判断.
如果你去商店时,向北走了400米,回来时你应该向东走400米.
6.一个平行四边形的底为15cm,高为5.5cm,如果图形按3:1扩大,那么扩大后的图形面积是247.5cm2 . ( ??)
7.一个图形放大或缩小后,大小发生了变化,形状没变。
8.判断对错. 一个图形按1∶10缩小就是把这个图形的面积缩小为原来的 .
三、填空题
9.钓鱼岛及其附属岛屿自古就是中国的领土,钓鱼岛距温岭市松门镇约390千米。在一幅地图上量出是3厘米,这幅地图的比例尺是________。
10.把地面150千米的距离用5厘米的线段画在地图上,那么,这幅地图的比例尺是________.
11.一幅地图的比例尺是1:5000000,这是________比例尺,图上1厘米表示实际距离________千米.在这地图上量得A、B两地距离是6厘米,实际距离是________千米.
12.如下图,将△EDC放大一定比例成△ABC,直角△DCE的三条边分别是3cm、4cm、5cm。如果AB=6cm,那么AE=________cm。
四、解答题
13.下图是一个飞机场的雷达屏幕,每相邻两个圆之间的距离是10千米(最里面的小圆的半径为10千米),以机场为观测点,在图中标出各飞机所在的位置。
①飞机A在机场的北偏西60°方向40千米处。
②飞机B在机场的北偏东30°方向20千米处。
③飞机C在机场的南偏西30°方向30千米处。
④飞机D在机场的南偏东60°方向60千米处。
14.根据已知条件,在图中画出指定场所的位置. ⑴阳光社区在中心花园东偏北30°的方向,距离中心花园3.5千米. ⑵体育场在中心花园南偏西45°的方向,距离中心花园2千米. ⑶公交车总站在中心花园南偏东35°的方向,距离中心花园4千米. ⑷幼儿园在中心花园西偏南15°的方向,距离中心花园3千米.
五、综合题
15.看图填空
(1)教学楼在操场的________,图书室在操场的________,大门在操场的________,体育馆在操场的________.
(2)图书馆在教学楼的________,体育馆在教学楼的________
六、应用题
16.小东家到学校的实际距离约300米,在地图上的距离是1.5厘米,这幅地图的比例尺是多少?这幅地图上小东家到少年宫的图上距离是2.5厘米,实际距离是多少米?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】东北方也叫作北偏东
【分析】考察了学生根据方向和距离确定物体位置的能力
2.【答案】 C
【解析】【解答】解:3×2=6(厘米)
6×6=36(平方厘米)
答:放大后的正方形的面积是36平方厘米.
故选:C.
【分析】把边长3厘米的正方形按2:1放大后,边长是3×2=6厘米,再利用正方形的面积公式即可解答.本题根据放大与缩小的方法,得出放大后的正方形的边长是解决本题的关键.
3.【答案】C
【解析】【解答】解因为50千米=5000000厘米,
则1厘米:5000000厘米=1:5000000;
【分析】因为图上距离1厘米表示实际距离50千米,化成同一单位后,再据比例尺的意义,即可得解。
故选:C
4.【答案】 C
【解析】【解答】解:令甲乙两圆的图上直径为2d,3d,
根据比例尺可得实际甲乙两圆的直径分别是2d×8=16d,3d×8=24d,
16d:24d=2:3.
故选:C.
【分析】根据比例尺的意义,令甲乙两圆的图上直径为2d,3d,根据比例尺可得实际圆的直径分别是16d,24d,由此利用比例尺进行计算,即可选择正确答案.
二、判断题
5.【答案】 错误
【解析】
6.【答案】 错误
【解析】【解答】(15×3)×(5.5×3) =45×16.5 =742.5(cm2) 原题说法错误。 故答案为:错误。 【分析】根据题意可知,先求出扩大后的平行四边形的底与高,然后用扩大后的底×高=扩大后的平行四边形面积,据此列式解答。
7.【答案】 错误
【解析】【解答】解:如果一个图形的每一部分不是按照一定的比例放大或缩小,那么这个图形不光大小会发生变化,形状也会发生变化。 故答案为:错误。 【分析】把一个图形按一定的比例放大或缩小后,大小发生了变化,形状没变。
8.【答案】错误
【解析】【解答】解:设原正方形边长是1厘米,面积是1×1=1平方厘米; 一个正方形按1:10缩小后,正方形边长是1×(1:10)=1×=厘米,正方形面积=×=平方厘米; ÷1=,所以面积缩小为原来的;所以一个图形按1:10缩小就是把这个图形的面积缩小为原来的说法错误。 故答案为:错误。 【分析】本题先设原正方形边长是1厘米,求出原正方形面积,再根据图上距离=实际距离×比例尺,求出按1:10缩小后,正方形边长和面积是多少,然后进行比较面积的变化,即可解答此题。
三、填空题
9.【答案】1:13000000
【解析】【解答】解:390千米=39000000厘米,比例尺:3:39000000=1:13000000. 故答案为:1:13000000 【分析】先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可求出比例尺.
10.【答案】1:3000000
【解析】【解答】解:150千米=15000000厘米 5:15000000=1:3000000 答:这幅地图的比例尺是1:3000000. 故答案为:1:3000000. 【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比.
11.【答案】数值;50;300
【解析】【解答】解:(1)比例尺是1:5000000,这是数值比例尺,图上1厘米表示实际距离5000000厘米,即50千米;(2)6÷ =30000000(厘米)=300(千米); 故答案为:数值,50,300. 【分析】(1)比例尺是1:5000000,这是数值比例尺,图上1厘米表示实际距离5000000厘米,即50千米;(2)图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出A、B两地之间的实际距离.此题主要考查比例尺的意义以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算.
12.【答案】 5
【解析】【解答】6÷3=2, 5×2-5 =10-5 =5(cm). 故答案为:5. 【分析】观察图可知,△EDC中的直角边ED=3cm,放大后变成了AB,AB=6cm,则放大的比例是6:3=2:1;则放大后斜边AC的长度是:5×2=10cm,AE=AC-EC=10-5=5cm,据此解答. ?
四、解答题
13.【答案】 解:
【解析】【解答】根据分析,作图如下:
【分析】根据图可知,图中是按“上北下南,左西右东”来规定方向的,根据条件“ 每相邻两个圆之间的距离是10千米(最里面的小圆的半径为10千米) ”,以机场为观测点,依据各飞机在机场的方位和距离作图即可.
14.【答案】解:
【解析】【解答】根据分析,作图如下: 【分析】解答此题应该先确定比例尺,根据图意,可以用图上1厘米表示实际1千米,根据方向和距离的描述作图即可.
五、综合题
15.【答案】(1)北面;东面;南面;西面 (2)东南;西南
【解析】【解答】解:(1)教学楼在操场的 北面,图书室在操场的 东面,大门在操场的 南面,体育馆在操场的 西面.(2)图书馆在教学楼的 东南,体育馆在教学楼的 西南;
故答案为:北面,东面,南面,西面,东南,西南.
【分析】平面图中的方向标是:上北、下南、左西、右东,由此即可确定上图中的物体的位置.
六、应用题
16.【答案】解:因为300米=30000厘米, 则1.5厘米:30000厘米=1:20000; 答:这幅地图的比例尺是1:20000; 2.5÷ =50000(厘米), 50000厘米=500米; 答:实际距离是500米.
【解析】【分析】(1)图上距离和实际距离已知,依据“比例尺= ,代入数值,即可求得这幅图的比例尺;(2)求小东家到少年宫的实际距离,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可.解答此题应根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论.
