六年级上册数学一课一练-3.3探索规律 西师大版 (含答案)
文档属性
| 名称 | 六年级上册数学一课一练-3.3探索规律 西师大版 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 47.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 18:48:31 | ||
图片预览


文档简介
六年级上册数学一课一练-3.3探索规律
一、单选题
1.循环小数0.02567的小数点后第2012位上的数字是( )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
2.化成小数后,小数点右边第200位上的数是( )
A.?4???????????????????????????????????????????B.?2???????????????????????????????????????????C.?8???????????????????????????????????????????D.?5
3.加法算式1+2,2+5,3+8,1+11,2+14,3+17,……是按一定规律排列的,则第40个加法算式是(??? )。
A.?1+120????????????????????????????????B.?2+119????????????????????????????????C.?1+199????????????????????????????????D.?2+120
二、填空题
4.9876-6789=3087;
6543-3456=3087;
3210-123=3087;
7654-4567=________
5.2003名学生从前往后排成一列,按下面的规则报数,如果某个同学报的数是一位数,后面的同学就在报出这个数与9的和,如果某个同学报的数是二位数,后面的同学就要报出这个数的个位数与6的和,现让第一个同学报2,那么最后一个同学所报的数是________?.
6.找规律填一填。?????????????????????????????
(1)3、7、11、________、________。
(2)19、17、15、________、________。
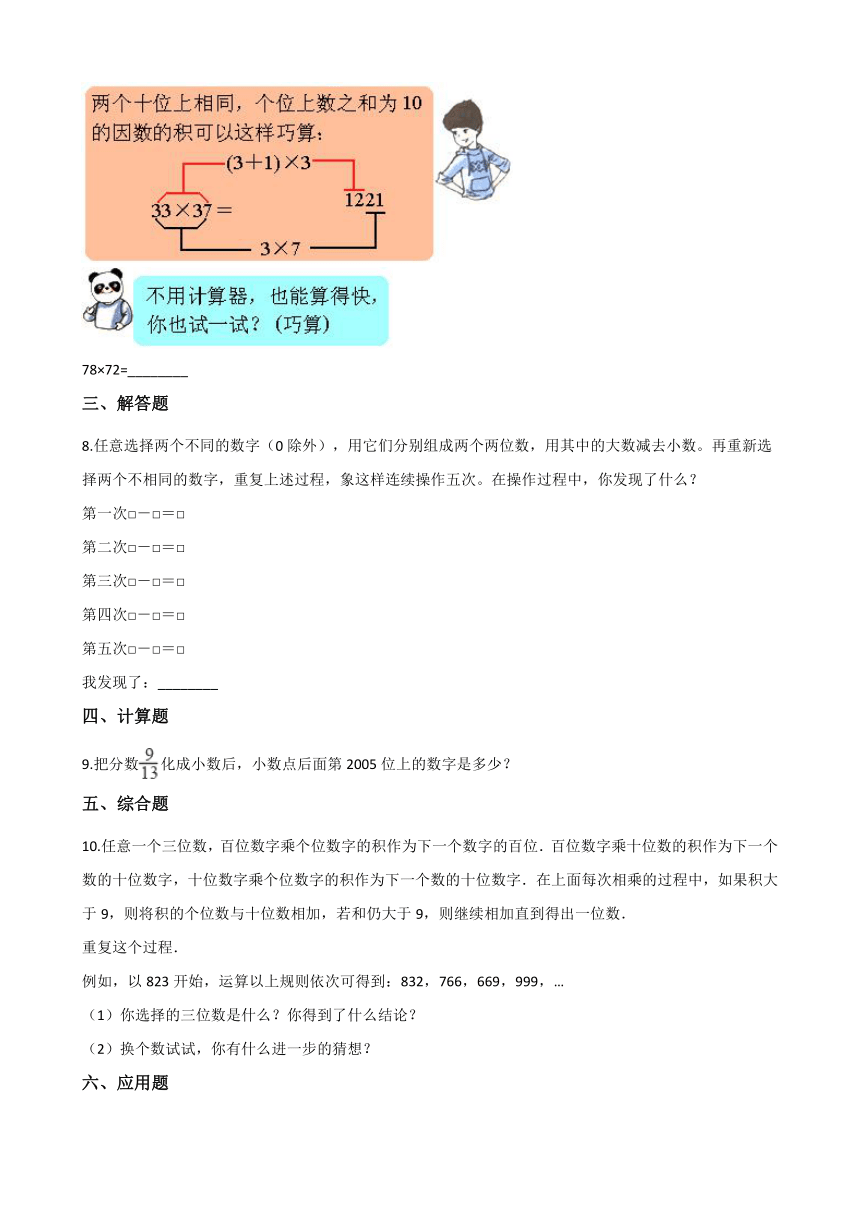
7.计算
15×15=225
34×36=1224
25×25=625
33×37=1221
35×35=1225
32×38=1216
45×45=2025
31×39=1209
78×72=________
三、解答题
8.任意选择两个不同的数字(0除外),用它们分别组成两个两位数,用其中的大数减去小数。再重新选择两个不相同的数字,重复上述过程,象这样连续操作五次。在操作过程中,你发现了什么? 第一次□-□=□ 第二次□-□=□ 第三次□-□=□ 第四次□-□=□ 第五次□-□=□ 我发现了:________
四、计算题
9.把分数化成小数后,小数点后面第2005位上的数字是多少?
五、综合题
10.任意一个三位数,百位数字乘个位数字的积作为下一个数字的百位.百位数字乘十位数的积作为下一个数的十位数字,十位数字乘个位数字的积作为下一个数的十位数字.在上面每次相乘的过程中,如果积大于9,则将积的个位数与十位数相加,若和仍大于9,则继续相加直到得出一位数.
重复这个过程.
例如,以823开始,运算以上规则依次可得到:832,766,669,999,…
(1)你选择的三位数是什么?你得到了什么结论?
(2)换个数试试,你有什么进一步的猜想?
六、应用题
11.1÷7的商是循环小数,这个小数的小数点右边第100位上 的数字是多少?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:0.02567的循环节是5位数, ÷5=402;
那么小数点后第2012位上的数字是循环节的末位上的数字,也就是8;
故选:D.
【分析】用2012减去2除以循环节的位数,如果能整除,第2012位上的数字是循环节末位上的数字;如果不能整除,余数是几,就从循环节的首位,数出几位,该位上的数字就是第2012位上的数字;由此解答.
2.【答案】 B
【解析】【解答】解:=0.2857, 它每6个数字一个循环:4、2、8、5、7、1;
200÷6=33…2.因为余数是2,所以小数点右第200位上的数字是2.
故选:B.
【分析】先把化成小数,=2857, 它每6个数字一个循环,用200除以6,再根据它的商和余数确定200位上的数.
3.【答案】 C
【解析】【解答】解:40÷3=13……1,第一个加数是“1、2、3”中的第一个是1; 第二个加数: 2+(40-1)×3 =2+117 =119 所以第40个加法算式是1+119 故答案为:C
【分析】第一个加数是“1、2、3”三个数字循环,用40除以3求出商和余数,余数是几就说明第40个算式中的第一个加数与“1、2、3”中的第几个数字相同;第二个加数依次多3,第40个算式中第二个加数比2多(40-1)个3,由此计算出第二个加数即可。
二、填空题
4.【答案】3087
【解析】【解答】7654-4567=3087 故答案为:3087
【分析】观察所给算式可以看出:被减数和减数是由四个连续自然数组成的最大数和最小数,不管这几个数字是多少,它们的差都是3087。
5.【答案】15
【解析】【解答】解:因为从第二名开始循环,每一个循环占13名同学,报数分别为11、7、16、12、8、17、13、9、18、14、10、6、15, 所以 ÷13=154, 对应的一个循环中的第13个数是15, 故答案为:15. 【分 析】只分析前几位同学报的数就可以发现规律:第一名同学报2,第二名同学报2+9=11,第三名同学报1+6=7,第四名同学报7+9=16,第五名同学 报6+6=12,第六名同学报2+6=8,第七名同学报8+9=17,第八名同学报7+6=13,第九名同学报3+6=9,第十名同学报9+9=18,第 十一名同学报8+6=14,第十二名同学报4+6=10,第十三名同学报0+6=6,第十四名同学报6+9=15,第十五名同学报5+6=11,第十六名 同学报1+6=7…依次算下去,分别报数为2、11、7、16、12、8、17、13、9、18、14、10、6、15、11、7…其实我们不难发现除了 第一个数2外,是11、7、16、12、8、17、13、9、18、14、10、6、15这13个数为一个循环,即从第二名开始循环,每一个循环占13名 同学,所以 ÷13看余数是几就是对应的一个循环中的第几个数.
6.【答案】(1)15;19 (2)13;11
【解析】
7.【答案】5616
【解析】【解答】解:78×72=5616 故答案为:5616 【分析】两位数乘两位数,两个因数个位数字的和是10,十位数字相同。两个个位数字的乘积就是得数的后两位数字,“十位数字×(十位数字+1)”就是得数前两位或前一位数字,按照这样的规律计算即可。
三、解答题
8.【答案】第一组:这两个数是8和5,那么: 85-58=27,27÷(8-5)=9; 第二组:1和7; 71-17=54,54÷(7-1)=9; 第三组:5和2; 52-25=27,27÷(5-2)=9; 第四组:6和3; 63-36=27,27÷(6-3)=9; 第五组:9和2; 92-29=63,63÷(9-2)=9 规律:每一次的结果都是两个数字差的9倍。
【解析】【分析】根据题意,用举例的方法解答,对于任何数设原两位数的十位数字为b,个位数字为a(b>a),则原两位数为10b+a,交换后的两位数为10a+b; 10b+a-(10a+b)=9(b-a)是9的倍数,由此可见这两个两位数的差都是这两个数字差的9倍,且对任何数都成立.
四、计算题
9.【答案】解:=0.9230, 循环节是692307有6个数字, 2005÷6=334(个)…1, 所以第2005位上是第335个循环节的第1位数字,是6. 答:小数点后面第2005位上的数字是6.
【解析】【分析】因为=0.9230该结果是循环小数,它的循环节是692307,是6位数,2005÷6=334(个)…1,所以小数部分的第2005位数字是334个循环节后的335个循环节上的第1个数字,循环节692307的第1个数字是6,据此解答.
五、综合题
10.【答案】(1)解:我选择的三位数是123,运算以上规则依次可得到:326,963,999,999,999…
(2)解:看题上的规律,999后边还是999;而我第(2)步举得例子也是999,
?看来根据题中规律,总是会得到一个相同的三位数999.
答:我选择的三位数是123,运算以上规则依次可得到:326,963,999,999,999…;看来根据题中规律,总是会得到一个相同的三位数999.
【解析】【分析】通过分析可知运算规律:百位数字乘个位数字的积作为下一个数字的百位.百位数字乘十位数的积作为下一个数的十位数字,十位数字乘个位数字的积作为 下一个数的十位数字.在上面每次相乘的过程中,如果积大于9,则将积的个位数与十位数相加,若和仍大于9,则急需相加直到得出一位数,据此解答即可.
六、应用题
11.【答案】解:1÷7=0.142857142857··· ? 答:这个小数的小数点右边第100位上的数字是8
【解析】【分析】循环节原有六个数字,即六个数字循环一次,100说明循环节一共循环了16次还多4个数字,也就是循环第17次时的第4个数字
一、单选题
1.循环小数0.02567的小数点后第2012位上的数字是( )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
2.化成小数后,小数点右边第200位上的数是( )
A.?4???????????????????????????????????????????B.?2???????????????????????????????????????????C.?8???????????????????????????????????????????D.?5
3.加法算式1+2,2+5,3+8,1+11,2+14,3+17,……是按一定规律排列的,则第40个加法算式是(??? )。
A.?1+120????????????????????????????????B.?2+119????????????????????????????????C.?1+199????????????????????????????????D.?2+120
二、填空题
4.9876-6789=3087;
6543-3456=3087;
3210-123=3087;
7654-4567=________
5.2003名学生从前往后排成一列,按下面的规则报数,如果某个同学报的数是一位数,后面的同学就在报出这个数与9的和,如果某个同学报的数是二位数,后面的同学就要报出这个数的个位数与6的和,现让第一个同学报2,那么最后一个同学所报的数是________?.
6.找规律填一填。?????????????????????????????
(1)3、7、11、________、________。
(2)19、17、15、________、________。
7.计算
15×15=225
34×36=1224
25×25=625
33×37=1221
35×35=1225
32×38=1216
45×45=2025
31×39=1209
78×72=________
三、解答题
8.任意选择两个不同的数字(0除外),用它们分别组成两个两位数,用其中的大数减去小数。再重新选择两个不相同的数字,重复上述过程,象这样连续操作五次。在操作过程中,你发现了什么? 第一次□-□=□ 第二次□-□=□ 第三次□-□=□ 第四次□-□=□ 第五次□-□=□ 我发现了:________
四、计算题
9.把分数化成小数后,小数点后面第2005位上的数字是多少?
五、综合题
10.任意一个三位数,百位数字乘个位数字的积作为下一个数字的百位.百位数字乘十位数的积作为下一个数的十位数字,十位数字乘个位数字的积作为下一个数的十位数字.在上面每次相乘的过程中,如果积大于9,则将积的个位数与十位数相加,若和仍大于9,则继续相加直到得出一位数.
重复这个过程.
例如,以823开始,运算以上规则依次可得到:832,766,669,999,…
(1)你选择的三位数是什么?你得到了什么结论?
(2)换个数试试,你有什么进一步的猜想?
六、应用题
11.1÷7的商是循环小数,这个小数的小数点右边第100位上 的数字是多少?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:0.02567的循环节是5位数, ÷5=402;
那么小数点后第2012位上的数字是循环节的末位上的数字,也就是8;
故选:D.
【分析】用2012减去2除以循环节的位数,如果能整除,第2012位上的数字是循环节末位上的数字;如果不能整除,余数是几,就从循环节的首位,数出几位,该位上的数字就是第2012位上的数字;由此解答.
2.【答案】 B
【解析】【解答】解:=0.2857, 它每6个数字一个循环:4、2、8、5、7、1;
200÷6=33…2.因为余数是2,所以小数点右第200位上的数字是2.
故选:B.
【分析】先把化成小数,=2857, 它每6个数字一个循环,用200除以6,再根据它的商和余数确定200位上的数.
3.【答案】 C
【解析】【解答】解:40÷3=13……1,第一个加数是“1、2、3”中的第一个是1; 第二个加数: 2+(40-1)×3 =2+117 =119 所以第40个加法算式是1+119 故答案为:C
【分析】第一个加数是“1、2、3”三个数字循环,用40除以3求出商和余数,余数是几就说明第40个算式中的第一个加数与“1、2、3”中的第几个数字相同;第二个加数依次多3,第40个算式中第二个加数比2多(40-1)个3,由此计算出第二个加数即可。
二、填空题
4.【答案】3087
【解析】【解答】7654-4567=3087 故答案为:3087
【分析】观察所给算式可以看出:被减数和减数是由四个连续自然数组成的最大数和最小数,不管这几个数字是多少,它们的差都是3087。
5.【答案】15
【解析】【解答】解:因为从第二名开始循环,每一个循环占13名同学,报数分别为11、7、16、12、8、17、13、9、18、14、10、6、15, 所以 ÷13=154, 对应的一个循环中的第13个数是15, 故答案为:15. 【分 析】只分析前几位同学报的数就可以发现规律:第一名同学报2,第二名同学报2+9=11,第三名同学报1+6=7,第四名同学报7+9=16,第五名同学 报6+6=12,第六名同学报2+6=8,第七名同学报8+9=17,第八名同学报7+6=13,第九名同学报3+6=9,第十名同学报9+9=18,第 十一名同学报8+6=14,第十二名同学报4+6=10,第十三名同学报0+6=6,第十四名同学报6+9=15,第十五名同学报5+6=11,第十六名 同学报1+6=7…依次算下去,分别报数为2、11、7、16、12、8、17、13、9、18、14、10、6、15、11、7…其实我们不难发现除了 第一个数2外,是11、7、16、12、8、17、13、9、18、14、10、6、15这13个数为一个循环,即从第二名开始循环,每一个循环占13名 同学,所以 ÷13看余数是几就是对应的一个循环中的第几个数.
6.【答案】(1)15;19 (2)13;11
【解析】
7.【答案】5616
【解析】【解答】解:78×72=5616 故答案为:5616 【分析】两位数乘两位数,两个因数个位数字的和是10,十位数字相同。两个个位数字的乘积就是得数的后两位数字,“十位数字×(十位数字+1)”就是得数前两位或前一位数字,按照这样的规律计算即可。
三、解答题
8.【答案】第一组:这两个数是8和5,那么: 85-58=27,27÷(8-5)=9; 第二组:1和7; 71-17=54,54÷(7-1)=9; 第三组:5和2; 52-25=27,27÷(5-2)=9; 第四组:6和3; 63-36=27,27÷(6-3)=9; 第五组:9和2; 92-29=63,63÷(9-2)=9 规律:每一次的结果都是两个数字差的9倍。
【解析】【分析】根据题意,用举例的方法解答,对于任何数设原两位数的十位数字为b,个位数字为a(b>a),则原两位数为10b+a,交换后的两位数为10a+b; 10b+a-(10a+b)=9(b-a)是9的倍数,由此可见这两个两位数的差都是这两个数字差的9倍,且对任何数都成立.
四、计算题
9.【答案】解:=0.9230, 循环节是692307有6个数字, 2005÷6=334(个)…1, 所以第2005位上是第335个循环节的第1位数字,是6. 答:小数点后面第2005位上的数字是6.
【解析】【分析】因为=0.9230该结果是循环小数,它的循环节是692307,是6位数,2005÷6=334(个)…1,所以小数部分的第2005位数字是334个循环节后的335个循环节上的第1个数字,循环节692307的第1个数字是6,据此解答.
五、综合题
10.【答案】(1)解:我选择的三位数是123,运算以上规则依次可得到:326,963,999,999,999…
(2)解:看题上的规律,999后边还是999;而我第(2)步举得例子也是999,
?看来根据题中规律,总是会得到一个相同的三位数999.
答:我选择的三位数是123,运算以上规则依次可得到:326,963,999,999,999…;看来根据题中规律,总是会得到一个相同的三位数999.
【解析】【分析】通过分析可知运算规律:百位数字乘个位数字的积作为下一个数字的百位.百位数字乘十位数的积作为下一个数的十位数字,十位数字乘个位数字的积作为 下一个数的十位数字.在上面每次相乘的过程中,如果积大于9,则将积的个位数与十位数相加,若和仍大于9,则急需相加直到得出一位数,据此解答即可.
六、应用题
11.【答案】解:1÷7=0.142857142857··· ? 答:这个小数的小数点右边第100位上的数字是8
【解析】【分析】循环节原有六个数字,即六个数字循环一次,100说明循环节一共循环了16次还多4个数字,也就是循环第17次时的第4个数字
