三年级下册数学一课一练-4.3建筑中的对称 西师大版(含答案)
文档属性
| 名称 | 三年级下册数学一课一练-4.3建筑中的对称 西师大版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 91.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 00:00:00 | ||
图片预览


文档简介
三年级下册数学一课一练-4.3建筑中的对称
一、单选题
1.美丽的图案都用到了(?? )
A.?平移??????????????????????????????????B.?旋转??????????????????????????????????C.?平移、旋转和对称
2.小明用如下图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的四个图案中,符合图示胶滚涂出的图案是(?? )
A.?A???????????????????????????????????????????B.?B???????????????????????????????????????????C.?C???????????????????????????????????????????D.?D
3.把一张圆形的纸对折,再对折,再对折,所形成的角是( )度。
A.?30????????????????????????????????????????????B.?45????????????????????????????????????????????C.?90
二、判断题
4.利用平移、旋转和轴对称,可以设计出许多美丽的图案。( ???)
5.利用平移、对称可以设计许多美丽的图案。
6.角的边越长,角就越大。
三、填空题
7.图形在平移和旋转后,________发生了变化,________不变。
8.图形变换包括________、________和________等。
9.由________组成
10.一个等边三角形绕它的一个顶点旋转90°后,变成了不等边三角形,这种情况可能出现吗?(填可能或不可能)________
四、解答题
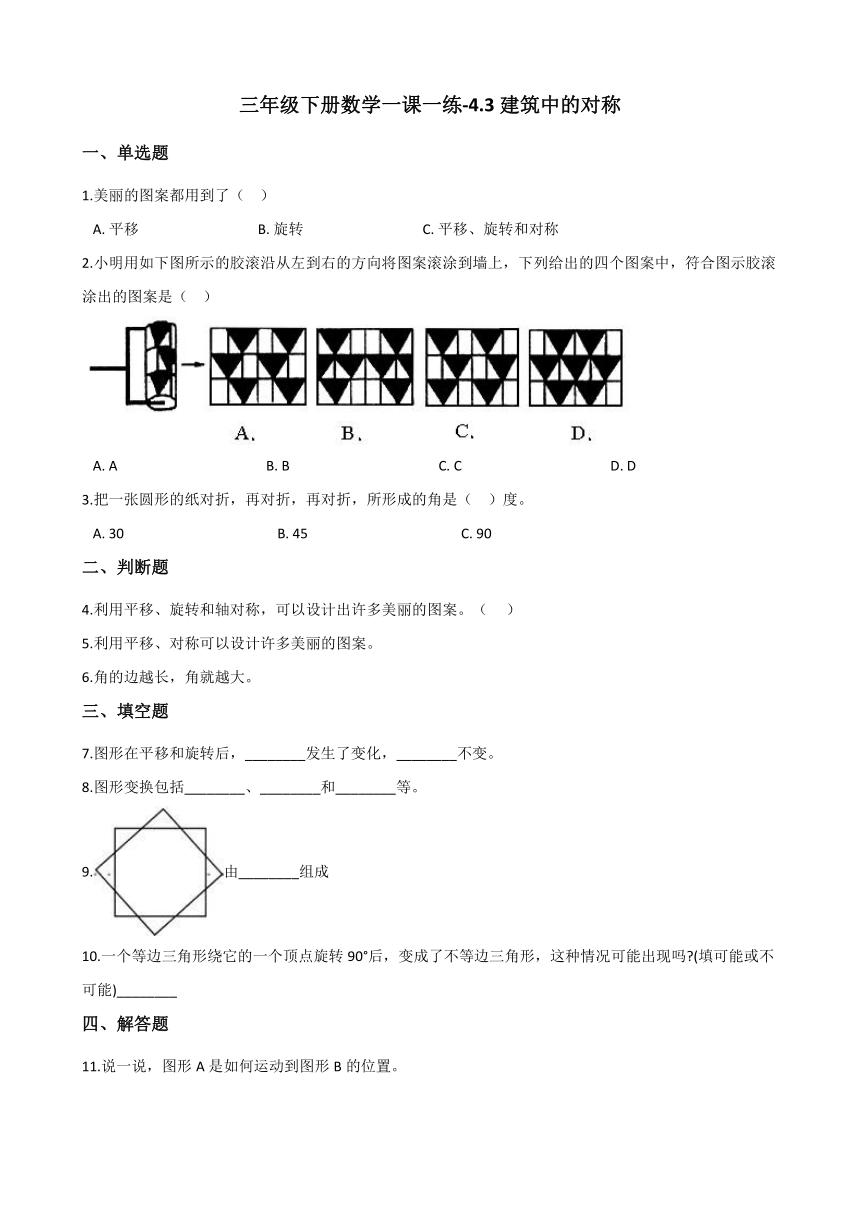
11.说一说,图形A是如何运动到图形B的位置。
12.自己按一定的规律设计一组图形,让同学来找一找规律。
五、综合题
13.画一画
?
(1)把图①向右平移4格,画出平移后的图形。
(2)把图②绕B点顺时针旋转90°,再右平移5格。画出旋转、平移的图形。
(3)把图③先向上平移1格,再绕A点逆时针旋转90°,再向右平移4格。
(4)把图④先向左平移4格,再绕O点逆时针旋转90°
六、应用题
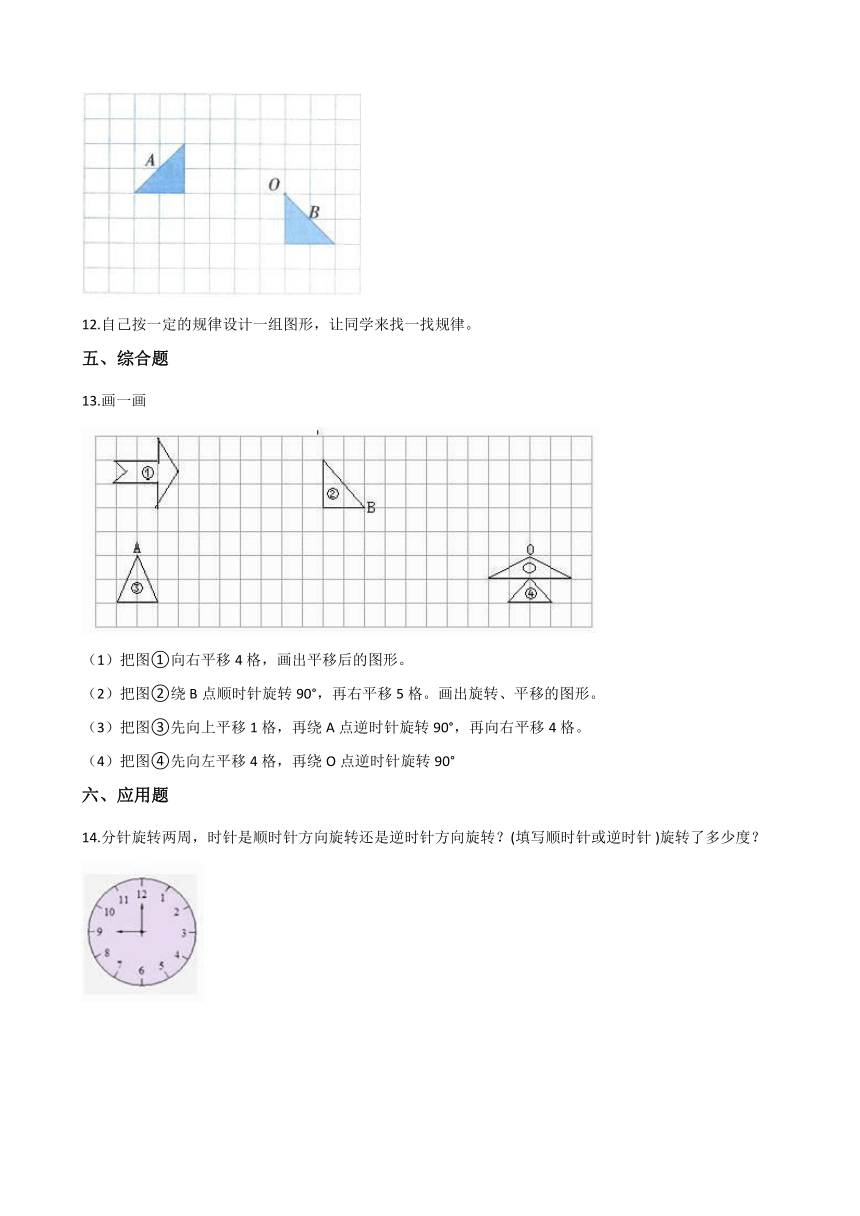
14.分针旋转两周,时针是顺时针方向旋转还是逆时针方向旋转?(填写顺时针或逆时针?)旋转了多少度?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】美丽的图案的设计一般都用到了平移、旋转和对称原理 【分析】考查了判别美丽的图案设计运用的平移、对称和旋转原理
2.【答案】 A
【解析】【解答】根据旋转的特征可得到图形A是符合题意的。 故答案为:A。
【分析】根据题意可知,第一行和第三行的图形是完全相同的,是图形是两两相对的关系。
3.【答案】 B
【解析】【解答】把一张圆形的纸对折,再对折,再对折,所形成的角是45度。
【分析】圆形的纸是周角,对折一次是平角,对折两次是周角,对折三次是45度。本题考查旋转与角。
二、判断题
4.【答案】 正确
【解析】【解答】解:利用平移、旋转和轴对称,可以设计出许多美丽的图案。原题说法正确。 故答案为:正确。 【分析】许多图案都是由一些规则的图形经过平移、旋转和轴对称得到的。
5.【答案】正确
【解析】【解答】解:根据分析画图如下: 故答案为:正确. 【分析】利用平移、对称可以设计许多美丽的图案,如先在图中画一个小旗,然后根据旋转图形的特征,将图中的小旗绕点O顺(或逆)时针旋转90°,点O的位置不动,其余各边都绕点O旋转90°,再旋转90°,再旋转90°即可得到如图美丽的图案.此题考查了运用平移、对称和旋转设计图案.
6.【答案】错误
【解析】【解答】角的边越长,角不一定越大。 故答案为:错误 【分析】角的边长度和角的大小没关系。
三、填空题
7.【答案】位置;大小、形状
【解析】【解答】解:图形在平移和旋转后,位置发生了变化,大小、形状不变。 故答案为:位置;大小、形状
【分析】平移和旋转都不改变图形的大小和形状,只是改变了图形的位置。
8.【答案】对称;平移;旋转
【解析】【解答】图形变换包括对称、平移和旋转等. 故答案为:对称;平移;旋转.【分析】轴对称变换:由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,轴对称变换不改变原图形的形状和大小;平移变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫做图形的平移变换,简称平移;旋转变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都围绕一个固定的点按同一个方向,旋转同一个角度,这样的图形改变叫做图形的旋转变换,简称旋转.
9.【答案】平行四边形
【解析】【解答】根据平行四边形的特点求解
10.【答案】不可能
【解析】【解答】解:一个等边三角形绕它的一个顶点旋转90°后,变成了不等边三角形,这种情况不可能出现。 故答案为:不可能 【分析】要想知道这种情况是否能出现,就要正确理解旋转的特征和性质。图形旋转后,形状、大小都没有发生变化,只是位置变了.图形中的对应角、对应线段都旋转相应的度数,和原图形相同。因此一个等边三角形旋转90°后,还是一个等边三角形,形状不会发生变化。
四、解答题
11.【答案】图形A先向右平移4格,再向下平移2格,然后顺时针旋转90°得到图形B.
【解析】【分析】图形的平移是由平移的方向和平移距离决定的,先找准对应点,然后判断平移的方向和距离,据此判断图形的变化;判断三角形旋转的角度,挑选三角形中的其中一条连着旋转点的边,这条边与旋转完后的边之间的夹角度数就是该图形旋转的角度,据此解答.
12.【答案】 解:如图:
【解析】【分析】这个图形就是一个梯形旋转四次设计出的图形。
五、综合题
13.【答案】(1) (2) (3) (4)
【解析】【分析】平移作图的步骤:1.找出能表示图形的关键点;2.确定平移的方向和距离;3.按平移的方向和距离确定关键点平移后的对应点;4.按原图的顺序,连接各对应点;画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接,据此作图即可.
六、应用题
14.【答案】解:因为分针旋转了两周,时针从9点走到11点,走了两个小格。每个小格的度数是360÷12=30(度),所以时针顺时针旋转了:30×2=60(度)。
【解析】
一、单选题
1.美丽的图案都用到了(?? )
A.?平移??????????????????????????????????B.?旋转??????????????????????????????????C.?平移、旋转和对称
2.小明用如下图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的四个图案中,符合图示胶滚涂出的图案是(?? )
A.?A???????????????????????????????????????????B.?B???????????????????????????????????????????C.?C???????????????????????????????????????????D.?D
3.把一张圆形的纸对折,再对折,再对折,所形成的角是( )度。
A.?30????????????????????????????????????????????B.?45????????????????????????????????????????????C.?90
二、判断题
4.利用平移、旋转和轴对称,可以设计出许多美丽的图案。( ???)
5.利用平移、对称可以设计许多美丽的图案。
6.角的边越长,角就越大。
三、填空题
7.图形在平移和旋转后,________发生了变化,________不变。
8.图形变换包括________、________和________等。
9.由________组成
10.一个等边三角形绕它的一个顶点旋转90°后,变成了不等边三角形,这种情况可能出现吗?(填可能或不可能)________
四、解答题
11.说一说,图形A是如何运动到图形B的位置。
12.自己按一定的规律设计一组图形,让同学来找一找规律。
五、综合题
13.画一画
?
(1)把图①向右平移4格,画出平移后的图形。
(2)把图②绕B点顺时针旋转90°,再右平移5格。画出旋转、平移的图形。
(3)把图③先向上平移1格,再绕A点逆时针旋转90°,再向右平移4格。
(4)把图④先向左平移4格,再绕O点逆时针旋转90°
六、应用题
14.分针旋转两周,时针是顺时针方向旋转还是逆时针方向旋转?(填写顺时针或逆时针?)旋转了多少度?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】美丽的图案的设计一般都用到了平移、旋转和对称原理 【分析】考查了判别美丽的图案设计运用的平移、对称和旋转原理
2.【答案】 A
【解析】【解答】根据旋转的特征可得到图形A是符合题意的。 故答案为:A。
【分析】根据题意可知,第一行和第三行的图形是完全相同的,是图形是两两相对的关系。
3.【答案】 B
【解析】【解答】把一张圆形的纸对折,再对折,再对折,所形成的角是45度。
【分析】圆形的纸是周角,对折一次是平角,对折两次是周角,对折三次是45度。本题考查旋转与角。
二、判断题
4.【答案】 正确
【解析】【解答】解:利用平移、旋转和轴对称,可以设计出许多美丽的图案。原题说法正确。 故答案为:正确。 【分析】许多图案都是由一些规则的图形经过平移、旋转和轴对称得到的。
5.【答案】正确
【解析】【解答】解:根据分析画图如下: 故答案为:正确. 【分析】利用平移、对称可以设计许多美丽的图案,如先在图中画一个小旗,然后根据旋转图形的特征,将图中的小旗绕点O顺(或逆)时针旋转90°,点O的位置不动,其余各边都绕点O旋转90°,再旋转90°,再旋转90°即可得到如图美丽的图案.此题考查了运用平移、对称和旋转设计图案.
6.【答案】错误
【解析】【解答】角的边越长,角不一定越大。 故答案为:错误 【分析】角的边长度和角的大小没关系。
三、填空题
7.【答案】位置;大小、形状
【解析】【解答】解:图形在平移和旋转后,位置发生了变化,大小、形状不变。 故答案为:位置;大小、形状
【分析】平移和旋转都不改变图形的大小和形状,只是改变了图形的位置。
8.【答案】对称;平移;旋转
【解析】【解答】图形变换包括对称、平移和旋转等. 故答案为:对称;平移;旋转.【分析】轴对称变换:由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,轴对称变换不改变原图形的形状和大小;平移变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫做图形的平移变换,简称平移;旋转变换:由一个图形改变为另一个图形,在改变过程中,原图形上所有的点都围绕一个固定的点按同一个方向,旋转同一个角度,这样的图形改变叫做图形的旋转变换,简称旋转.
9.【答案】平行四边形
【解析】【解答】根据平行四边形的特点求解
10.【答案】不可能
【解析】【解答】解:一个等边三角形绕它的一个顶点旋转90°后,变成了不等边三角形,这种情况不可能出现。 故答案为:不可能 【分析】要想知道这种情况是否能出现,就要正确理解旋转的特征和性质。图形旋转后,形状、大小都没有发生变化,只是位置变了.图形中的对应角、对应线段都旋转相应的度数,和原图形相同。因此一个等边三角形旋转90°后,还是一个等边三角形,形状不会发生变化。
四、解答题
11.【答案】图形A先向右平移4格,再向下平移2格,然后顺时针旋转90°得到图形B.
【解析】【分析】图形的平移是由平移的方向和平移距离决定的,先找准对应点,然后判断平移的方向和距离,据此判断图形的变化;判断三角形旋转的角度,挑选三角形中的其中一条连着旋转点的边,这条边与旋转完后的边之间的夹角度数就是该图形旋转的角度,据此解答.
12.【答案】 解:如图:
【解析】【分析】这个图形就是一个梯形旋转四次设计出的图形。
五、综合题
13.【答案】(1) (2) (3) (4)
【解析】【分析】平移作图的步骤:1.找出能表示图形的关键点;2.确定平移的方向和距离;3.按平移的方向和距离确定关键点平移后的对应点;4.按原图的顺序,连接各对应点;画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接,据此作图即可.
六、应用题
14.【答案】解:因为分针旋转了两周,时针从9点走到11点,走了两个小格。每个小格的度数是360÷12=30(度),所以时针顺时针旋转了:30×2=60(度)。
【解析】
