五年级下册数学一课一练-3.6设计长方体的包装方案 西师大版 (含答案)
文档属性
| 名称 | 五年级下册数学一课一练-3.6设计长方体的包装方案 西师大版 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 42.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 00:00:00 | ||
图片预览


文档简介
五年级下册数学一课一练-3.6设计长方体的包装方案
一、单选题
1.把一个正方体的棱长扩大2倍,则它的体积(?? )
A.?扩大2倍?????????????????????????????B.?扩大4倍?????????????????????????????C.?扩大8倍?????????????????????????????D.?扩大12倍
2.一个正方体的棱长扩大到原来的3倍,它的体积就扩大到原来的(??? )。
A.?3倍??????????????????????????????????????B.?9倍??????????????????????????????????????C.?6倍??????????????????????????????????????D.?27倍
3.将两个完全一样的长方体拼成一个大长方体,下列说法正确的是(?? )。
A.?表面积增加,体积不变???????????????????????????????????????B.?表面积减少,体积不变 C.?表面积和体积都增加???????????????????????????????????????????D.?表面积和体积都不变。
4.一个长方体的长、宽、高都扩大到原来的5倍,表面积就扩大到原来的(??? )倍。
A.?25?????????????????????????????????????????????B.?15?????????????????????????????????????????????C.?5
二、判断题
5.判断对错. 一个正方体的棱长扩大2倍,体积就扩大8倍.
6.将一个正方体切成两个完全相同的长方体,每个长方体的表面积是正方体表面积的一半.
7.正方体的棱长扩大2倍,则表面积和体积都扩大4倍.(判断对错)
8.判断对错.两个体积相等的长方体,它们的长、宽、高一定相等
三、填空题
9.棱长是1厘米的正方体,体积是________,记作________。
10.一个长方体水箱,底面长0.4米,宽30厘米,如果注水62.5厘米高,注入了________升水。
11.正方体的棱长之和是36厘米,正方体的表面积是________平方厘米,体积是________立方厘米.
12.在一个底面边长是2分米的正方体玻璃水槽中放入一块青铜(完全浸没在水中),水面上升1分米.(玻璃的厚度忽略不计)
(1)这块青铜的体积是________立方分米?
(2)如果每立方分米青铜重8.5千克,这块青铜重________千克?
(3)这块青铜是由铜、锡、锌按30∶3∶1铸造而成的,这块青铜中含铜、锡、锌各________千克?
(4)如果把这块青铜铸造成一个底面直径是10厘米的圆柱,它的高约是________厘米?(保留整数)
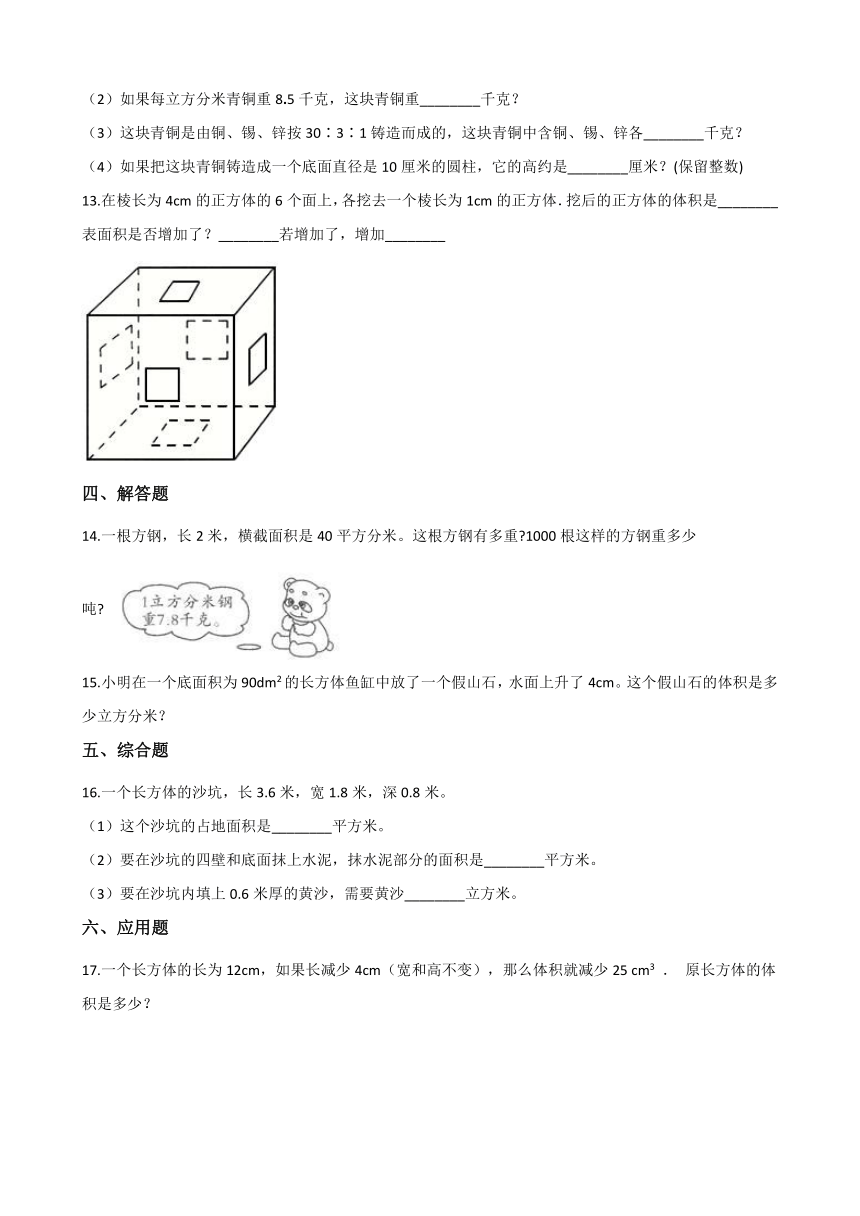
13.在棱长为4cm的正方体的6个面上,各挖去一个棱长为1cm的正方体.挖后的正方体的体积是________表面积是否增加了?________若增加了,增加________
四、解答题
14.一根方钢,长2米,横截面积是40平方分米。这根方钢有多重?1000根这样的方钢重多少吨?
15.小明在一个底面积为90dm2的长方体鱼缸中放了一个假山石,水面上升了4cm。这个假山石的体积是多少立方分米?
五、综合题
16.一个长方体的沙坑,长3.6米,宽1.8米,深0.8米。
(1)这个沙坑的占地面积是________平方米。
(2)要在沙坑的四壁和底面抹上水泥,抹水泥部分的面积是________平方米。
(3)要在沙坑内填上0.6米厚的黄沙,需要黄沙________立方米。
六、应用题
17.一个长方体的长为12cm,如果长减少4cm(宽和高不变),那么体积就减少25 cm3 . 原长方体的体积是多少?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:设原来的正方体的棱长是x,则后来的正方体的棱长是2x,
则(2x)3÷x3
=8x3÷x3
=8
所以把一个正方体的棱长扩大2倍,则它的体积扩大8倍.
故选:C.
【分析】设原来的正方体的棱长是x,则后来的正方体的棱长是2x,根据“正方体的体积=棱长3”分别求出原来、后来两个正方体的体积,然后根据求一个数是另一个数的几倍用除法解答即可.
2.【答案】D
【解析】【解答】解:设正方体的棱长为a,扩大到原来的3倍为:3a. 因原正方体的体积=a×a×a=;扩大后的正方体的面积=3a3a3a=27,故选 D。 【分析】正方体积的大小,取决于棱长:棱长越长体积越大,棱长越短体积越小。若棱长扩大3倍,就等于体积扩大了:3×3×3=27(倍),据此可求解。
3.【答案】 B
【解析】【解答】解:两个完全一样的长方体拼成一个大长方体,长方体表面积减少,体积不变. 故答案为:B.
【分析】两个完全一样的长方体拼成一个大长方体,减少两个面的面积,体积不因形状改变而改变,据此解答即可.
4.【答案】 A
【解析】【解答】一个长方体的长、宽、高分别扩大到原来的5倍,表面积就扩大5×5=25倍,
答:表面积就扩大到原来的25倍。故选A。
【分析】根据长方体的表面积公式:s=〔ab+ah+bh)×2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答。
二、判断题
5.【答案】正确
【解析】【解答】一个正方体的棱长扩大2倍,体积就扩大:2×2×2=8倍,原题说法正确. 故答案为:正确. 【分析】正方体的体积=棱长×棱长×棱长,据此分析解答.
6.【答案】错误
【解析】【解答】解:正方体切成两个完全相同的长方体后,表面积比原来增加了两个正方体的面的面积, 所以每个长方体的表面积是原来的正方体的表面积的一半加上一个正方体的面的面积, 所以原题说法错误. 故答案为:错误. 【分析】正方体切成两个完全相同的长方体后,表面积比原来增加了两个正方体的面的面积,由此即可进行判断.解答此题要明确:正方体切成两个完全相同的长方体后表面积比原来增加了两个面的面积.
7.【答案】正确
【解析】【解答】解:正方体的棱长扩大2倍,它的表面积就扩大2×2=4倍. 因此,正方体的棱长扩大2倍,则表面积和体积都扩大4倍.这种说法是正确的. 故答案为:正确. 【分析】根据正方体的表面积公式:s=6a2 , 再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断即可.
8.【答案】错误
【解析】【解答】因为长方体体积=长×宽×高,所以两个体积相等的长方体,它们的长、宽、高不一定相等,本题错 故答案为:错误 【分析】体积相等,只能说明长×宽×高的积相等,并不能说明它们的长、宽、高一定相等
三、填空题
9.【答案】1立方厘米;1cm3
【解析】【解答】棱长是1厘米的正方体,体积是:1×1×1=1(立方厘米),记作:1cm3 故答案为:1立方厘米;1cm3 【分析】正方体的体积=棱长×棱长×棱长,据此列式解答.
10.【答案】 75
【解析】【解答】解:0.4米=40厘米 40×30×62.5=75000(立方厘米)=75立方分米=75升 故答案为:75。
【分析】长方体体积=长×宽×高,代入数据计算即可求出水的体积。
11.【答案】54;27
【解析】【解答】解:36÷12=3(厘米) 表面积:3×3×6=54(平方厘米) 体积:3×3×3=27(立方厘米) 故答案为:54;27 【分析】用正方体棱长之和除以12即可求出正方体棱长,正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6.
12.【答案】(1)4 (2)34 (3)30;3;1 (4)51
【解析】【解答】解:(1)青铜的体积:2×2×1=4(立方分米); (2)青铜的重量:4×8.5=34(千克); (3)铜:34×=30(千克); 锡:34×=3(千克); 锌:34×=1(千克); (4)4立方分米=4000立方厘米,10÷2=5(厘米) 4000÷(3.14×52) =4000÷78.5 ≈51(厘米) 故答案为:4;34;30;3;1;51
【分析】(1)水面上升部分水的体积就是青铜的体积;(2)用青铜的体积乘8.5即可求出青铜的重量;(3)把青铜的重量按照30:3:1的比例分配后分别求出三种成分的重量即可;(4)把青铜的体积换算成立方厘米,然后用青铜的体积除以铸造的圆柱的底面积即可求出圆柱的高.
13.【答案】58立方厘米;是增加了;24平方厘米
【解析】【解答】解:体积: 4×4×4-1×1×1×6 =64-6 =58(立方厘米) 表面积增加了:1×1×4×6=24(平方厘米) 故答案为:58立方厘米;是增加了;24平方厘米 【分析】用大正方体的体积减去6个小正方体的体积就是剩下的体积;每挖去一个小正方体就会增加四个小正方形的面,因此表面积是增加的,计算出增加的小正方形面的个数即可计算增加的面积.
四、解答题
14.【答案】解:2米=20分米40×20×7.8=6240(千克) 6240×1000=6240000(千克)=6240(吨) 答:这根方钢有6240千克,1000根这样的方钢重6240吨。
【解析】【分析】根据长方体的体积=底面积高先算出方钢的体积,再用方钢的体积乘1立方分米的方钢的质量即可算出1根方钢的质量,用1根方钢的质量乘1000即可算出1000根这样的方钢的重量
15.【答案】解:4cm=0.4dm,90×0.4=36(dm3) 答:这假山石的体积是36立方分米。
【解析】【分析】假山石是浸没在水中的,水面上升部分水的体积就是假山石的体积,由此用鱼缸的底面积乘水面上升的高度即可求出假山石的体积。
五、综合题
16.【答案】(1)6.48 (2)15.12 (3)3.888
【解析】【解答】解:(1)3.6×1.8=6.48(平方米); (2)6.48+1.8×0.8×2+3.6×0.8×2 =6.48+2.88+5.76 =15.12(平方米) (3)6.48×0.6=3.888(立方米) 故答案为:6.48;15.12;3.888
【分析】(1)根据长方形面积公式计算占地面积;(2)用底面积加上左右和前后面的面积就是抹水泥的面积;(3)用占地面积乘黄沙的厚度即可求出黄沙的体积.
六、应用题
17.【答案】解:25÷4×12 =6.25×12 =75(立方厘米) 答:原长方体的体积是75立方厘米.
【解析】【分析】由题意,长减少4厘米,体积就减少25立方厘米,可知宽×高×4=25立方厘米,则宽×高=6.25平方厘米.再根据长方体的体积公式:V=abh,解答即可.
一、单选题
1.把一个正方体的棱长扩大2倍,则它的体积(?? )
A.?扩大2倍?????????????????????????????B.?扩大4倍?????????????????????????????C.?扩大8倍?????????????????????????????D.?扩大12倍
2.一个正方体的棱长扩大到原来的3倍,它的体积就扩大到原来的(??? )。
A.?3倍??????????????????????????????????????B.?9倍??????????????????????????????????????C.?6倍??????????????????????????????????????D.?27倍
3.将两个完全一样的长方体拼成一个大长方体,下列说法正确的是(?? )。
A.?表面积增加,体积不变???????????????????????????????????????B.?表面积减少,体积不变 C.?表面积和体积都增加???????????????????????????????????????????D.?表面积和体积都不变。
4.一个长方体的长、宽、高都扩大到原来的5倍,表面积就扩大到原来的(??? )倍。
A.?25?????????????????????????????????????????????B.?15?????????????????????????????????????????????C.?5
二、判断题
5.判断对错. 一个正方体的棱长扩大2倍,体积就扩大8倍.
6.将一个正方体切成两个完全相同的长方体,每个长方体的表面积是正方体表面积的一半.
7.正方体的棱长扩大2倍,则表面积和体积都扩大4倍.(判断对错)
8.判断对错.两个体积相等的长方体,它们的长、宽、高一定相等
三、填空题
9.棱长是1厘米的正方体,体积是________,记作________。
10.一个长方体水箱,底面长0.4米,宽30厘米,如果注水62.5厘米高,注入了________升水。
11.正方体的棱长之和是36厘米,正方体的表面积是________平方厘米,体积是________立方厘米.
12.在一个底面边长是2分米的正方体玻璃水槽中放入一块青铜(完全浸没在水中),水面上升1分米.(玻璃的厚度忽略不计)
(1)这块青铜的体积是________立方分米?
(2)如果每立方分米青铜重8.5千克,这块青铜重________千克?
(3)这块青铜是由铜、锡、锌按30∶3∶1铸造而成的,这块青铜中含铜、锡、锌各________千克?
(4)如果把这块青铜铸造成一个底面直径是10厘米的圆柱,它的高约是________厘米?(保留整数)
13.在棱长为4cm的正方体的6个面上,各挖去一个棱长为1cm的正方体.挖后的正方体的体积是________表面积是否增加了?________若增加了,增加________
四、解答题
14.一根方钢,长2米,横截面积是40平方分米。这根方钢有多重?1000根这样的方钢重多少吨?
15.小明在一个底面积为90dm2的长方体鱼缸中放了一个假山石,水面上升了4cm。这个假山石的体积是多少立方分米?
五、综合题
16.一个长方体的沙坑,长3.6米,宽1.8米,深0.8米。
(1)这个沙坑的占地面积是________平方米。
(2)要在沙坑的四壁和底面抹上水泥,抹水泥部分的面积是________平方米。
(3)要在沙坑内填上0.6米厚的黄沙,需要黄沙________立方米。
六、应用题
17.一个长方体的长为12cm,如果长减少4cm(宽和高不变),那么体积就减少25 cm3 . 原长方体的体积是多少?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:设原来的正方体的棱长是x,则后来的正方体的棱长是2x,
则(2x)3÷x3
=8x3÷x3
=8
所以把一个正方体的棱长扩大2倍,则它的体积扩大8倍.
故选:C.
【分析】设原来的正方体的棱长是x,则后来的正方体的棱长是2x,根据“正方体的体积=棱长3”分别求出原来、后来两个正方体的体积,然后根据求一个数是另一个数的几倍用除法解答即可.
2.【答案】D
【解析】【解答】解:设正方体的棱长为a,扩大到原来的3倍为:3a. 因原正方体的体积=a×a×a=;扩大后的正方体的面积=3a3a3a=27,故选 D。 【分析】正方体积的大小,取决于棱长:棱长越长体积越大,棱长越短体积越小。若棱长扩大3倍,就等于体积扩大了:3×3×3=27(倍),据此可求解。
3.【答案】 B
【解析】【解答】解:两个完全一样的长方体拼成一个大长方体,长方体表面积减少,体积不变. 故答案为:B.
【分析】两个完全一样的长方体拼成一个大长方体,减少两个面的面积,体积不因形状改变而改变,据此解答即可.
4.【答案】 A
【解析】【解答】一个长方体的长、宽、高分别扩大到原来的5倍,表面积就扩大5×5=25倍,
答:表面积就扩大到原来的25倍。故选A。
【分析】根据长方体的表面积公式:s=〔ab+ah+bh)×2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答。
二、判断题
5.【答案】正确
【解析】【解答】一个正方体的棱长扩大2倍,体积就扩大:2×2×2=8倍,原题说法正确. 故答案为:正确. 【分析】正方体的体积=棱长×棱长×棱长,据此分析解答.
6.【答案】错误
【解析】【解答】解:正方体切成两个完全相同的长方体后,表面积比原来增加了两个正方体的面的面积, 所以每个长方体的表面积是原来的正方体的表面积的一半加上一个正方体的面的面积, 所以原题说法错误. 故答案为:错误. 【分析】正方体切成两个完全相同的长方体后,表面积比原来增加了两个正方体的面的面积,由此即可进行判断.解答此题要明确:正方体切成两个完全相同的长方体后表面积比原来增加了两个面的面积.
7.【答案】正确
【解析】【解答】解:正方体的棱长扩大2倍,它的表面积就扩大2×2=4倍. 因此,正方体的棱长扩大2倍,则表面积和体积都扩大4倍.这种说法是正确的. 故答案为:正确. 【分析】根据正方体的表面积公式:s=6a2 , 再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断即可.
8.【答案】错误
【解析】【解答】因为长方体体积=长×宽×高,所以两个体积相等的长方体,它们的长、宽、高不一定相等,本题错 故答案为:错误 【分析】体积相等,只能说明长×宽×高的积相等,并不能说明它们的长、宽、高一定相等
三、填空题
9.【答案】1立方厘米;1cm3
【解析】【解答】棱长是1厘米的正方体,体积是:1×1×1=1(立方厘米),记作:1cm3 故答案为:1立方厘米;1cm3 【分析】正方体的体积=棱长×棱长×棱长,据此列式解答.
10.【答案】 75
【解析】【解答】解:0.4米=40厘米 40×30×62.5=75000(立方厘米)=75立方分米=75升 故答案为:75。
【分析】长方体体积=长×宽×高,代入数据计算即可求出水的体积。
11.【答案】54;27
【解析】【解答】解:36÷12=3(厘米) 表面积:3×3×6=54(平方厘米) 体积:3×3×3=27(立方厘米) 故答案为:54;27 【分析】用正方体棱长之和除以12即可求出正方体棱长,正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6.
12.【答案】(1)4 (2)34 (3)30;3;1 (4)51
【解析】【解答】解:(1)青铜的体积:2×2×1=4(立方分米); (2)青铜的重量:4×8.5=34(千克); (3)铜:34×=30(千克); 锡:34×=3(千克); 锌:34×=1(千克); (4)4立方分米=4000立方厘米,10÷2=5(厘米) 4000÷(3.14×52) =4000÷78.5 ≈51(厘米) 故答案为:4;34;30;3;1;51
【分析】(1)水面上升部分水的体积就是青铜的体积;(2)用青铜的体积乘8.5即可求出青铜的重量;(3)把青铜的重量按照30:3:1的比例分配后分别求出三种成分的重量即可;(4)把青铜的体积换算成立方厘米,然后用青铜的体积除以铸造的圆柱的底面积即可求出圆柱的高.
13.【答案】58立方厘米;是增加了;24平方厘米
【解析】【解答】解:体积: 4×4×4-1×1×1×6 =64-6 =58(立方厘米) 表面积增加了:1×1×4×6=24(平方厘米) 故答案为:58立方厘米;是增加了;24平方厘米 【分析】用大正方体的体积减去6个小正方体的体积就是剩下的体积;每挖去一个小正方体就会增加四个小正方形的面,因此表面积是增加的,计算出增加的小正方形面的个数即可计算增加的面积.
四、解答题
14.【答案】解:2米=20分米40×20×7.8=6240(千克) 6240×1000=6240000(千克)=6240(吨) 答:这根方钢有6240千克,1000根这样的方钢重6240吨。
【解析】【分析】根据长方体的体积=底面积高先算出方钢的体积,再用方钢的体积乘1立方分米的方钢的质量即可算出1根方钢的质量,用1根方钢的质量乘1000即可算出1000根这样的方钢的重量
15.【答案】解:4cm=0.4dm,90×0.4=36(dm3) 答:这假山石的体积是36立方分米。
【解析】【分析】假山石是浸没在水中的,水面上升部分水的体积就是假山石的体积,由此用鱼缸的底面积乘水面上升的高度即可求出假山石的体积。
五、综合题
16.【答案】(1)6.48 (2)15.12 (3)3.888
【解析】【解答】解:(1)3.6×1.8=6.48(平方米); (2)6.48+1.8×0.8×2+3.6×0.8×2 =6.48+2.88+5.76 =15.12(平方米) (3)6.48×0.6=3.888(立方米) 故答案为:6.48;15.12;3.888
【分析】(1)根据长方形面积公式计算占地面积;(2)用底面积加上左右和前后面的面积就是抹水泥的面积;(3)用占地面积乘黄沙的厚度即可求出黄沙的体积.
六、应用题
17.【答案】解:25÷4×12 =6.25×12 =75(立方厘米) 答:原长方体的体积是75立方厘米.
【解析】【分析】由题意,长减少4厘米,体积就减少25立方厘米,可知宽×高×4=25立方厘米,则宽×高=6.25平方厘米.再根据长方体的体积公式:V=abh,解答即可.
