高中数学人教A版2003课标版必修1.1.2.1 函数的概念(共17张PPT)
文档属性
| 名称 | 高中数学人教A版2003课标版必修1.1.2.1 函数的概念(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
1.1 集合
1.1.1 集合的含义与表示(1课时)
1.1.2 集合间的基本关系(1课时)
1.1.3 集合的基本运算(1课时)
1.2 函数及其表示
1.2.1 函数的概念(1课时)
1.2.2 函数的表示方法(2课时)
1.3 函数的基本性质
1.3.1 函数的单调性与最大(小)值(2课时)
1.3.2 奇偶性(1课时)
第一章复习与测试
(1)课本从大家熟悉的集合出发,给出元素、集合的含义及表示方法;通过类比实数间的大小关系、运算引入集合间的关系、运算,同时介绍子集和全集等概念.
(2)函数是中学数学最重要的基本概念之一.函数分两阶段学习:(初中)函数概念、正(反)比例函数、一次函数、二次函数及其图像和性质.(高一必修)函数概念、基本性质、基本初等函数(I、II).(高二选修)导数及其应用.
(3)实习作业:收集17世纪前后对数学发展起重大作用的历史事件和人物(开普勒、伽利略、笛卡尔、牛顿、莱布尼兹、欧拉等)的有关资料.
本章内容简介
1.理解函数的概念,体会对应关系在刻画函数概念中的作用.
2.掌握构成函数的三要素,会求一些简单函数的定义域.
3.会用区间表示连续数集.
学习目标
设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有惟一的值与它对应,则称x是自变量,y是x的函数.
1.初中学习的函数概念是什么?
2.请问:我们在初中学过哪些函数?
一、初中的函数
时间t的变化范围是数集A={t|0≤t≤26},
高度h的变化范围是数集B={h|0≤h≤845}
对于数集A中的任意一个时刻t,按照对应关系h=130t-5t2,在数集B中都有惟一的高度h和它对应
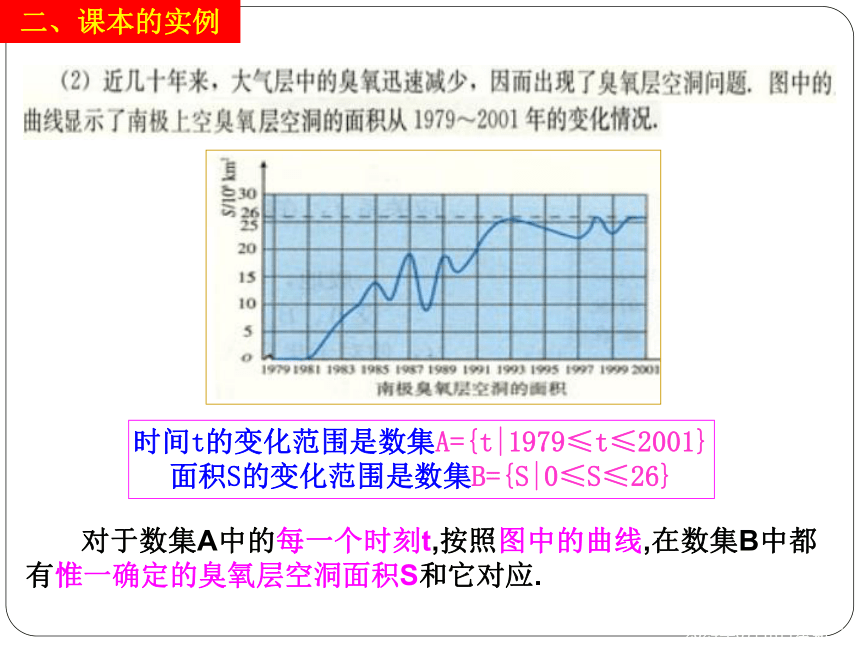
二、课本的实例
二、课本的实例
时间t的变化范围是数集A={t|1979≤t≤2001} 面积S的变化范围是数集B={S|0≤S≤26}
对于数集A中的每一个时刻t,按照图中的曲线,在数集B中都有惟一确定的臭氧层空洞面积S和它对应.
时间构成一个数集A,恩格尔系数构成一个数集B.
对于数集A中的每一个时刻t,按照表中的对应值,在数集B中都有惟一确定的恩格尔系数和它对应.
二、课本的实例
对于数集A中的每一个x,按照某种对应关系f ,在数集B中都有惟一确定的y和它对应,记作 f: A→B.
二、课本的实例
设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x) ,x∈A.
x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
初中各类函数的对应法则、定义域、值域分别是什么?
三、函数的概念
R
R
R
R
R
三、函数的概念
三、函数的概念
试用区间表示下列实数集合
(1) {x|5 ≤ x<6}
(2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
设a,b是两个实数,而且a(1) 满足不等式a≤x≤b的实数x的集合叫做闭区间,表示为 [a,b]
(2) 满足不等式a(1) 满足不等式a≤x 实数集R可以用区间表示为(-∞,+∞),“∞”读作“无穷大”.满足x≥a,x>a ,x≤b,x四、区间的概念
连续数集
①定义域是研究任何函数的前提 ②函数的定义域常常由其实际背景决定,若只给出解析式时,定义域就是使这个式子有意义的实数x的集合.
实数集R
使分母不等于0的实数的集合
使根号内的式子大于或等于0的实数的集合
使各部分式子都有意义的实数的集合(即各集合的交集)
使实际问题有意义的实数的集合
(3)如果y=f (x)是二次根式,则定义域是
(4)如果y=f (x)是由几个部分的式子构成的,则定义域是
(1)如果y=f (x)是整式,则定义域是
(2)如果y=f (x)是分式,则定义域是
(5)如果是实际问题,是
五、例题
如何判断两个函数是否相同?
五、例题
如果两个函数的定义域相同,对应关系完全一样,则称这两个函数相等.
五、例题
抽象函数的定义域
函数的解析式
五、例题
六、课后小结
1.1 集合
1.1.1 集合的含义与表示(1课时)
1.1.2 集合间的基本关系(1课时)
1.1.3 集合的基本运算(1课时)
1.2 函数及其表示
1.2.1 函数的概念(1课时)
1.2.2 函数的表示方法(2课时)
1.3 函数的基本性质
1.3.1 函数的单调性与最大(小)值(2课时)
1.3.2 奇偶性(1课时)
第一章复习与测试
(1)课本从大家熟悉的集合出发,给出元素、集合的含义及表示方法;通过类比实数间的大小关系、运算引入集合间的关系、运算,同时介绍子集和全集等概念.
(2)函数是中学数学最重要的基本概念之一.函数分两阶段学习:(初中)函数概念、正(反)比例函数、一次函数、二次函数及其图像和性质.(高一必修)函数概念、基本性质、基本初等函数(I、II).(高二选修)导数及其应用.
(3)实习作业:收集17世纪前后对数学发展起重大作用的历史事件和人物(开普勒、伽利略、笛卡尔、牛顿、莱布尼兹、欧拉等)的有关资料.
本章内容简介
1.理解函数的概念,体会对应关系在刻画函数概念中的作用.
2.掌握构成函数的三要素,会求一些简单函数的定义域.
3.会用区间表示连续数集.
学习目标
设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有惟一的值与它对应,则称x是自变量,y是x的函数.
1.初中学习的函数概念是什么?
2.请问:我们在初中学过哪些函数?
一、初中的函数
时间t的变化范围是数集A={t|0≤t≤26},
高度h的变化范围是数集B={h|0≤h≤845}
对于数集A中的任意一个时刻t,按照对应关系h=130t-5t2,在数集B中都有惟一的高度h和它对应
二、课本的实例
二、课本的实例
时间t的变化范围是数集A={t|1979≤t≤2001} 面积S的变化范围是数集B={S|0≤S≤26}
对于数集A中的每一个时刻t,按照图中的曲线,在数集B中都有惟一确定的臭氧层空洞面积S和它对应.
时间构成一个数集A,恩格尔系数构成一个数集B.
对于数集A中的每一个时刻t,按照表中的对应值,在数集B中都有惟一确定的恩格尔系数和它对应.
二、课本的实例
对于数集A中的每一个x,按照某种对应关系f ,在数集B中都有惟一确定的y和它对应,记作 f: A→B.
二、课本的实例
设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x) ,x∈A.
x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
初中各类函数的对应法则、定义域、值域分别是什么?
三、函数的概念
R
R
R
R
R
三、函数的概念
三、函数的概念
试用区间表示下列实数集合
(1) {x|5 ≤ x<6}
(2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
设a,b是两个实数,而且a
(2) 满足不等式a
连续数集
①定义域是研究任何函数的前提 ②函数的定义域常常由其实际背景决定,若只给出解析式时,定义域就是使这个式子有意义的实数x的集合.
实数集R
使分母不等于0的实数的集合
使根号内的式子大于或等于0的实数的集合
使各部分式子都有意义的实数的集合(即各集合的交集)
使实际问题有意义的实数的集合
(3)如果y=f (x)是二次根式,则定义域是
(4)如果y=f (x)是由几个部分的式子构成的,则定义域是
(1)如果y=f (x)是整式,则定义域是
(2)如果y=f (x)是分式,则定义域是
(5)如果是实际问题,是
五、例题
如何判断两个函数是否相同?
五、例题
如果两个函数的定义域相同,对应关系完全一样,则称这两个函数相等.
五、例题
抽象函数的定义域
函数的解析式
五、例题
六、课后小结
