四年级下册数学一课一练-4.1认识三角形 西师大版(含答案)
文档属性
| 名称 | 四年级下册数学一课一练-4.1认识三角形 西师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 32.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
四年级下册数学一课一练-4.1认识三角形
一、单选题
1.一个三角形从它的一个顶点起,用一条直线把它分成两个小三角形,每个小三角形的内角和是(
)。
A. 90° B. 180° C. 360°
2.一个三角形至少有()个锐角.(
)
A. 1 B. 2 C. 3
3.一个三角形中最大角的度数是这个三角形内角和的
,这是一个( )三角形.
A. 锐角 B. 直角 C. 钝角
4.等腰三角形中有一个角是50°,另外两个内角(
)。
A. 都是65° B. 是50°和80° C. 是50°和80°或者都是65°
二、判断题
5.钝角三角形有内角和大于锐角三角形的内角和。
6.将一个大三角形分成两个小三角形,每个小三角形的内角和是90度。
7.慧眼识真金(判断正误)。
一个直角三角形中,一个锐角是20°,另一个锐角就是70°。
8.一个三角形可能有两个钝角。
三、填空题
9.一个三角形的三个内角和是________度.
10.求出下面三角形中未知角的度数.
________°
11.仔细想,认真填。
一个等腰三角形的一个底角是30°,它的顶角是________度。
12.仔细想,认真填。
在一个三角形中,一个内角是72°,另一个内角是58°,那么第三个内角是________°。
四、解答题
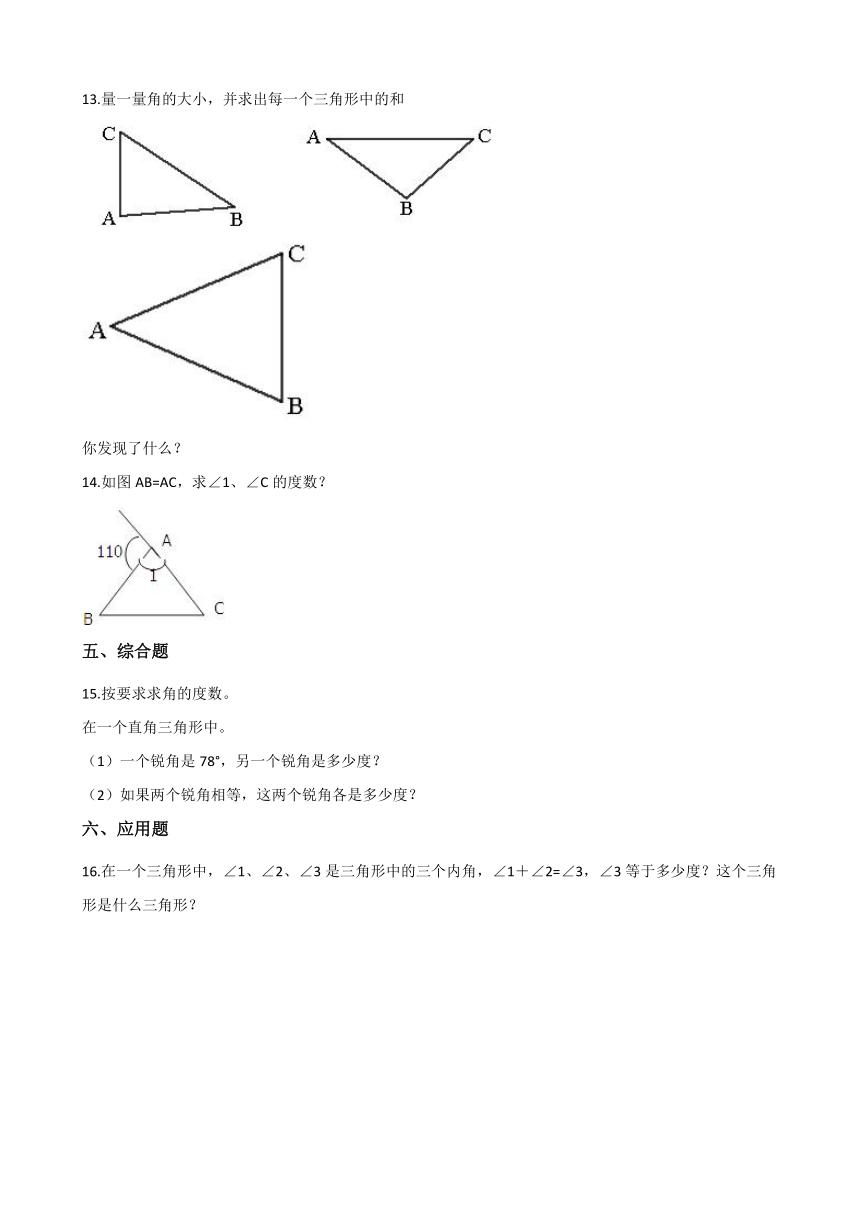
13.量一量角的大小,并求出每一个三角形中的和
你发现了什么?
14.如图AB=AC,求∠1、∠C的度数?
五、综合题
15.按要求求角的度数。
在一个直角三角形中。
(1)一个锐角是78°,另一个锐角是多少度?
(2)如果两个锐角相等,这两个锐角各是多少度?
六、应用题
16.在一个三角形中,∠1、∠2、∠3是三角形中的三个内角,∠1+∠2=∠3,∠3等于多少度?这个三角形是什么三角形?
参考答案
一、单选题
1.【答案】
B
【解析】【解答】三角形的内角和是180°.
故答案为:B.
【分析】任何一个三角形的内角和都是180°,据此解答.
2.【答案】
B
【解析】【解答】解:一个三角形最多有一个直角或一个钝角,另外两个角都是锐角,所以一个三角形至少有2个锐角.
故答案为:B
【分析】三角形内角和是180°,所以三角形至少有2个锐角,最多三个都是锐角.
3.【答案】
C
【解析】【解答】解:180×
=120(度)
答:这是一个钝角三角形。
【分析】根据三角形的内角和等于180度,一个三角形中最大角的度数是这个三角形内角和的
,用180×
=120度,根据三角形的分类标准判断三角形的类别即可。
故选:C.
4.【答案】
C
【解析】【解答】当50°是底角时,顶角为180°-50°-50°=80°,所以另两个角是50°和80°;当50°是顶角时,180°-50°=130°,130°2=65°,所以两个内角都是65°。
故答案为:C。
【分析]
等腰三角形的两个底角的度数相等。
二、判断题
5.【答案】错误
【解析】【解答】解:钝角三角形和锐角三角形的内角和是相等的,原题说法错误.
故答案为:错误
【分析】任何三角形的内角和都是180°,这是固定不变的,与三角形的形状和大小无关.
6.【答案】
错误
【解析】【解答】解:每个小三角形的内角和是180°,原题说法错误.
故答案为:错误
【分析】任意三角形的内角和都是180°,这是固定不变的.
7.【答案】
正确
【解析】【解答】解:20°+70°=90°,在一个直角三角形中,一个锐角是20°,另一个锐角就是70°,原题说法正确.
故答案为:正确
【分析】三角形内角和是180°,直角三角形中两个锐角的度数和是90°,由此判断即可.
8.【答案】
错误
【解析】【解答】钝三角形的中有一个角是钝角,钝角大于90°,两个钝角的和大于180°,三角形内角和是180°.
故答案为:错误.
【分析】三角形内角和是180°,两个钝角的和大于180°,所以在三角形中只能有一个钝角.
三、填空题
9.【答案】
180
【解析】【解答】一个三角形的三个内角和是180度.
故答案为:180
【分析】三角形的性质:三角形内角和是180度.
10.【答案】
137
【解析】【解答】解:180°-26°-17°
=154°-17°
=137°
故答案为:137
【分析】用三角形内角和180°减去两个已知角的度数即可求出第三个内角的度数.
11.【答案】120
【解析】【解答】解:180°-30°×2
=180°-60°
=120°
故答案为:120
【分析】等腰三角形两个底角相等,用三角形内角和180度减去两个底角的度数即可求出顶角的度数.
12.【答案】
50
【解析】【解答】解:180°-(72°+58°)
=180°-130°
=50°
故答案为:50
【分析】三角形内角和是180°,用三角形内角和减去另外两个已知角的度数即可求出第三个内角的度数.
四、解答题
13.【答案】
三角形三个内角的和=180°
每一个三角形的三个内角的和都是180度。
【解析】【分析】解答此题根据测量角的度数的方法,测量出每个角的度数,然后把每个三角形内的三个角的度数相加,最后得数结论,三角形的内角和是180度,解答此题的关键是测量每个角的度数要准确.
14.【答案】
解:∠1=180°﹣110°=70°
∠C=(180°﹣70°)÷2
=110°÷2
=55°
答:∠1是70°,∠C是55°
【解析】【分析】因为AB=AC,所以三角形ABC是等腰三角形,所以∠B=∠C,然后用180°﹣110°即可求出∠1的度数,然后根据等腰三角形的性质以及三角形内角和是180度即可求出∠C的度数.
五、综合题
15.【答案】(1)解:90°-78°=12°
答:另一个锐角是12°
(2)解:90°÷2=45°
答:两个锐角都是45°
【解析】【分析】(1)直角三角形的两个锐角的和是90度,90度-一个锐角度数=另一个锐角度数;(2)两个锐角的和是90度,且度数相等,这两个锐角都是45度。
六、应用题
16.【答案】解:∠1+∠2+∠3=180°
∠1+∠2=∠3,所以
∠3+∠3=180°,∠3=90°
答:∠3等于90°,这是一个直角三角形.
【解析】【分析】要判断一个三角形是什么三角形,必须先求出其中各角的度数.因为∠1+∠2+∠3=180°,∠1+∠2=∠3,所以∠3+∠3=180°,2个∠3是180°,即∠3=90°.然后根据最大角的度数确定三角形的类型即可.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
四年级下册数学一课一练-4.1认识三角形
一、单选题
1.一个三角形从它的一个顶点起,用一条直线把它分成两个小三角形,每个小三角形的内角和是(
)。
A. 90° B. 180° C. 360°
2.一个三角形至少有()个锐角.(
)
A. 1 B. 2 C. 3
3.一个三角形中最大角的度数是这个三角形内角和的
,这是一个( )三角形.
A. 锐角 B. 直角 C. 钝角
4.等腰三角形中有一个角是50°,另外两个内角(
)。
A. 都是65° B. 是50°和80° C. 是50°和80°或者都是65°
二、判断题
5.钝角三角形有内角和大于锐角三角形的内角和。
6.将一个大三角形分成两个小三角形,每个小三角形的内角和是90度。
7.慧眼识真金(判断正误)。
一个直角三角形中,一个锐角是20°,另一个锐角就是70°。
8.一个三角形可能有两个钝角。
三、填空题
9.一个三角形的三个内角和是________度.
10.求出下面三角形中未知角的度数.
________°
11.仔细想,认真填。
一个等腰三角形的一个底角是30°,它的顶角是________度。
12.仔细想,认真填。
在一个三角形中,一个内角是72°,另一个内角是58°,那么第三个内角是________°。
四、解答题
13.量一量角的大小,并求出每一个三角形中的和
你发现了什么?
14.如图AB=AC,求∠1、∠C的度数?
五、综合题
15.按要求求角的度数。
在一个直角三角形中。
(1)一个锐角是78°,另一个锐角是多少度?
(2)如果两个锐角相等,这两个锐角各是多少度?
六、应用题
16.在一个三角形中,∠1、∠2、∠3是三角形中的三个内角,∠1+∠2=∠3,∠3等于多少度?这个三角形是什么三角形?
参考答案
一、单选题
1.【答案】
B
【解析】【解答】三角形的内角和是180°.
故答案为:B.
【分析】任何一个三角形的内角和都是180°,据此解答.
2.【答案】
B
【解析】【解答】解:一个三角形最多有一个直角或一个钝角,另外两个角都是锐角,所以一个三角形至少有2个锐角.
故答案为:B
【分析】三角形内角和是180°,所以三角形至少有2个锐角,最多三个都是锐角.
3.【答案】
C
【解析】【解答】解:180×
=120(度)
答:这是一个钝角三角形。
【分析】根据三角形的内角和等于180度,一个三角形中最大角的度数是这个三角形内角和的
,用180×
=120度,根据三角形的分类标准判断三角形的类别即可。
故选:C.
4.【答案】
C
【解析】【解答】当50°是底角时,顶角为180°-50°-50°=80°,所以另两个角是50°和80°;当50°是顶角时,180°-50°=130°,130°2=65°,所以两个内角都是65°。
故答案为:C。
【分析]
等腰三角形的两个底角的度数相等。
二、判断题
5.【答案】错误
【解析】【解答】解:钝角三角形和锐角三角形的内角和是相等的,原题说法错误.
故答案为:错误
【分析】任何三角形的内角和都是180°,这是固定不变的,与三角形的形状和大小无关.
6.【答案】
错误
【解析】【解答】解:每个小三角形的内角和是180°,原题说法错误.
故答案为:错误
【分析】任意三角形的内角和都是180°,这是固定不变的.
7.【答案】
正确
【解析】【解答】解:20°+70°=90°,在一个直角三角形中,一个锐角是20°,另一个锐角就是70°,原题说法正确.
故答案为:正确
【分析】三角形内角和是180°,直角三角形中两个锐角的度数和是90°,由此判断即可.
8.【答案】
错误
【解析】【解答】钝三角形的中有一个角是钝角,钝角大于90°,两个钝角的和大于180°,三角形内角和是180°.
故答案为:错误.
【分析】三角形内角和是180°,两个钝角的和大于180°,所以在三角形中只能有一个钝角.
三、填空题
9.【答案】
180
【解析】【解答】一个三角形的三个内角和是180度.
故答案为:180
【分析】三角形的性质:三角形内角和是180度.
10.【答案】
137
【解析】【解答】解:180°-26°-17°
=154°-17°
=137°
故答案为:137
【分析】用三角形内角和180°减去两个已知角的度数即可求出第三个内角的度数.
11.【答案】120
【解析】【解答】解:180°-30°×2
=180°-60°
=120°
故答案为:120
【分析】等腰三角形两个底角相等,用三角形内角和180度减去两个底角的度数即可求出顶角的度数.
12.【答案】
50
【解析】【解答】解:180°-(72°+58°)
=180°-130°
=50°
故答案为:50
【分析】三角形内角和是180°,用三角形内角和减去另外两个已知角的度数即可求出第三个内角的度数.
四、解答题
13.【答案】
三角形三个内角的和=180°
每一个三角形的三个内角的和都是180度。
【解析】【分析】解答此题根据测量角的度数的方法,测量出每个角的度数,然后把每个三角形内的三个角的度数相加,最后得数结论,三角形的内角和是180度,解答此题的关键是测量每个角的度数要准确.
14.【答案】
解:∠1=180°﹣110°=70°
∠C=(180°﹣70°)÷2
=110°÷2
=55°
答:∠1是70°,∠C是55°
【解析】【分析】因为AB=AC,所以三角形ABC是等腰三角形,所以∠B=∠C,然后用180°﹣110°即可求出∠1的度数,然后根据等腰三角形的性质以及三角形内角和是180度即可求出∠C的度数.
五、综合题
15.【答案】(1)解:90°-78°=12°
答:另一个锐角是12°
(2)解:90°÷2=45°
答:两个锐角都是45°
【解析】【分析】(1)直角三角形的两个锐角的和是90度,90度-一个锐角度数=另一个锐角度数;(2)两个锐角的和是90度,且度数相等,这两个锐角都是45度。
六、应用题
16.【答案】解:∠1+∠2+∠3=180°
∠1+∠2=∠3,所以
∠3+∠3=180°,∠3=90°
答:∠3等于90°,这是一个直角三角形.
【解析】【分析】要判断一个三角形是什么三角形,必须先求出其中各角的度数.因为∠1+∠2+∠3=180°,∠1+∠2=∠3,所以∠3+∠3=180°,2个∠3是180°,即∠3=90°.然后根据最大角的度数确定三角形的类型即可.
