五年级下册数学一课一练-1.3合数、质数 西师大版(含答案)
文档属性
| 名称 | 五年级下册数学一课一练-1.3合数、质数 西师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 60.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览



文档简介
(
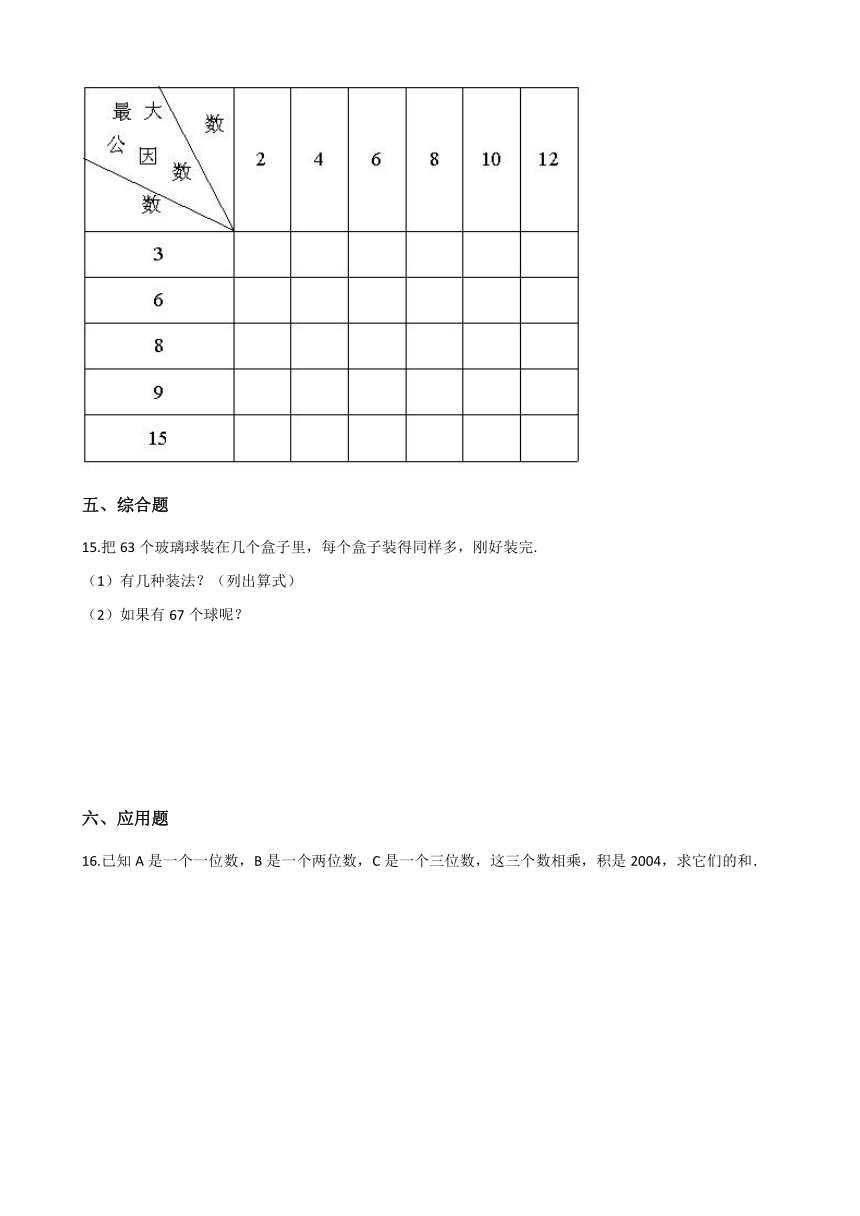
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-1.3合数、质数
一、单选题
1.下面的4个数中,(
)是奇数又是合数
A. 11 B. 13 C. 15 D. 17
2.a、b、c是三个不同的质数,且a>b,a+b=c,那么b=(
)
A. 2 B. 3 C. 5 D. 其它
3.两个质数相乘的积(
)。
A. 一定是偶数 B. 一定是合数 C. 可能是合数也可能是质数
4.在2至12中质数有(
)个。
A. 4 B. 6 C. 5 D. 3
二、判断题
5.判断对错.
相邻的两个数,一定是互质数.
6.在非0自然数中,除2以外,所有的偶数都是合数。
7.自然数中,是2的倍数的数叫做合数。
三、填空题
8.分解质因数
210=________×________×________×________
(从小到大依次填写)
9.在10以内的奇数中,所有质数的和是________
10.将6个“优秀少先队员”的名额分给六年级的一、二、三班,每个班至少1个名额,共有________ 种不同的分法.
11.非0自然数按能否被________整除,可以分成奇数和偶数;按约数的个数可以分成质数和________数.
12.100以内最大的质数与最小的合数的和是________,差是________。
四、解答题
13.把60分解质因数.
14.在下表中填出两个数的最大公因数.
五、综合题
15.把63个玻璃球装在几个盒子里,每个盒子装得同样多,刚好装完.
(1)有几种装法?(列出算式)
(2)如果有67个球呢?
六、应用题
16.已知A是一个一位数,B是一个两位数,C是一个三位数,这三个数相乘,积是2004,求它们的和.
参考答案
一、单选题
1.【答案】
C
【解析】【解答】因为,11、13和17是质数,15是合数,
故答案为:C.
【分析】根据合数与质数的认识进行解答.
2.【答案】
A
【解析】【解答】解:符合要求的只有3+2=5,所以b=2.
故答案为:A
【分析】从最小的质数开始试算,直到确定出符合a+b=c的算式就可以确定b的值.
3.【答案】
B
【解析】【解答】解:两个质数相乘的积,除了1和它本身外,这两个数也是它的因数。
故答案为:B
【分析】除了1和它本身外,还有别的因数的数是合数。
4.【答案】
C
【解析】【解答】在2至12中质数有2、3、5、7、11,共5个。
故答案为:C
【分析】质数:一个大于1的自然数,除了1和它本身外,不再有其他的因数,这样的数就是质数。
二、判断题
5.【答案】
错误
【解析】【解答】例如0和1是相邻的两个数,但它们不是互质数,所以原题说法错误.
故答案为:错误
【分析】互质数的定义:只有公因数1的两个数是互质数.采用举例子的方法是解答判断题常用的方法.
6.【答案】正确
【解析】【解答】解:在非0自然数列中,除2以外,所有的偶数的因数除了1和它本身以外,一定还有因数2,所以除了2以外的非0偶数都是合数.原题说法正确.
故答案为:正确【分析】合数是除了1和本身外还有其它因数的数,最小的合数是4,大于4的所有偶数都是合数,但是合数也有奇数.
7.【答案】
错误
【解析】【解答】解:例如2是2的倍数,但2是质数,原题说法错误.
故答案为:错误
【分析】合数是除了1和本身外还有其它因数的数,除了0、2之外,所有的偶数都是合数.
三、填空题
8.【答案】
2
;3
;5
;7
【解析】【解答】解:
210=2×3×5×7
故答案为:2,3,5,7.
【分析】根据短除法写出210的质因数进行解答.
9.【答案】15
【解析】【解答】解:10以内以内的奇数中,所有的质数有:3,5,7.
所以:10以内所有的质数的和是:3+5+7=15.
故答案为:15.
【分析】写出10以内的所有质数,再相加即可.
10.【答案】
10
【解析】【解答】解:由于每个班至少1个名额,6﹣3=3.
在每班保证一个的情况,还剩三个名额:
共有3×1+3×2+1=10(种).
答:共有10种不同的分法.
故答案为:10.
【分析】由于每个班至少1个名额,所以,本题的分配方案实质上就是对余下3个名额的分配方案:
(1)把3个名额都给一个班级:3种;
(2)将3个名额分成1个和2个进行分配共3×2=6种分法;
(1)将3个名额分成1、1、1进行分配共1种分法.即平均每班两个名额.
所以共有3+6+1=10种分法.
11.【答案】
2
;合
【解析】【解答】如果一个非0自然数能被2整除,这个数就是偶数,不能被2整除,这个数就是合数;一个数只有两个约数,这个数就是合数,至少有3个约数,这个数就是合数.
故答案为:2;合
【分析】偶数都能被2整除,奇数都不能被2整除;质数是只有1和本身两个因数的数,合数是除了1和本身外还有其他因数的数.
12.【答案】101;93
【解析】【解答】解:100以内最大的质数与最小的合数的和是101和93.
故答案为:101;93.
【分析】本题考查的主要内容是质数和合数的应用问题,根据质数和合数的定义进行分析.
四、解答题
13.【答案】
解:方法一:“树枝”图式分解法.
①先把60分解成两个数相乘形式,60分解成2×30.
②2是质数,不需再分解;30是合数,需再进行分解;直到所有因数是质数为止.
③写出分解结果.合数后面写等号,然后把分解出的质数用连乘形式写在等号后.
分解过程如图所示:
60=2×3×2×5
也可以先把60分解成6×10或4×15,然后再依次分解.如图:
60=3×2×5×2
60=2×2×3×5
从60的分解过程可以看出,60的质因数是2、3、2、5这四个数,分解过程中只是2、2、3、5的顺序不同.
方法二:短除法分解质因数.
①把要分解的数60写在短除号里.
②用60的质因数去除,一般从最小的质因数开始.
③直到商是质数为止.
④把除数和商写成相乘形式.
分解过程如下:
60=2×3×2×5
分解方式不仅有以上一种,还有其他分解方式,也可以按如下方式分解:
60=3×5×2×2
60=5×3×2×2
60=3×2×5×2
【解析】【分析】本题考查的主要内容是质因数的应用问题,根据质因数的定义进行分析.
14.【答案】解:
【解析】【解答】2和3的最大公因数是1;3和4的最大公因数是1;3和6的最大公因数是3;3和8的最大公因数是1;3和1的最大公因数是1;3和12的最大公因数是3;6和2的最大公因数是2;6和4的最大公因数是2;6和6的最大公因数是6;6和8的最大公因数是2;6和10的最大公因数是2;6和12的最大公因数是6;8和2的最大公因数是2;8和4的最大公因数是4;8和6的最大公因数是2;8和8的最大公因数是8;8和10的最大公因数是2;8和12的最大公因数是4;9和2的最大公因数是1;9和4的最大公因数是1;9和6的最大公因数是3;9和8的最大公因数是1;9和10的最大公因数是1;9和12的最大公因数是3;15和2的最大公因数是1;15和4的最大公因数是1;15和6的最大公因数是3;15和8的最大公因数是1;15和10的最大公因数是5;15和12的最大公因数是3.
故答案为:
【分析】两个数的最大公因数就是两个数公有的质因数的积;互质数的两个数的最大公因数是1;相邻的两个数的最大公因数是1.
五、综合题
15.【答案】
(1)解:63=1×63,每个盒子里装一个,或者将63个球装在一个盒子里,
63=3×21,每个盒子里装3个或每个盒子里装21个,
63=7×9,每个盒子里装7个或每个盒子里装9个,
装法有:2+2+2=6(种),
答:有6种不同的装法
(2)解:67是质数,所以只有2种装法:每个盒子里装一个,或者将67个球装在一个盒子里.
答:有2种装法
【解析】【分析】(1)根据题意,即把63个求平均分到若干个盒子里,那么两个数相乘积是63,因为没有规定盒子的个数,所有63有多少个因数就有几种装法,列式解答即可得到答案.(2)67是质数,所以67=1×67,由此即可得出只有2种不同的装法.解答此题关键将63和67进行分解因数,有几个因数就有几种装法.
六、应用题
16.【答案】
解:2004=2×2×3×167=1×12×167,
所以A=1,B=12,C=167
这三个数的和为:1+12+167=180,
答:它们的和为180
【解析】【分析】先把2004分解质因数得出A、B、C的值再相加即可.本题主要考查了合数分解质因数,关键是得出A、B、C的值.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-1.3合数、质数
一、单选题
1.下面的4个数中,(
)是奇数又是合数
A. 11 B. 13 C. 15 D. 17
2.a、b、c是三个不同的质数,且a>b,a+b=c,那么b=(
)
A. 2 B. 3 C. 5 D. 其它
3.两个质数相乘的积(
)。
A. 一定是偶数 B. 一定是合数 C. 可能是合数也可能是质数
4.在2至12中质数有(
)个。
A. 4 B. 6 C. 5 D. 3
二、判断题
5.判断对错.
相邻的两个数,一定是互质数.
6.在非0自然数中,除2以外,所有的偶数都是合数。
7.自然数中,是2的倍数的数叫做合数。
三、填空题
8.分解质因数
210=________×________×________×________
(从小到大依次填写)
9.在10以内的奇数中,所有质数的和是________
10.将6个“优秀少先队员”的名额分给六年级的一、二、三班,每个班至少1个名额,共有________ 种不同的分法.
11.非0自然数按能否被________整除,可以分成奇数和偶数;按约数的个数可以分成质数和________数.
12.100以内最大的质数与最小的合数的和是________,差是________。
四、解答题
13.把60分解质因数.
14.在下表中填出两个数的最大公因数.
五、综合题
15.把63个玻璃球装在几个盒子里,每个盒子装得同样多,刚好装完.
(1)有几种装法?(列出算式)
(2)如果有67个球呢?
六、应用题
16.已知A是一个一位数,B是一个两位数,C是一个三位数,这三个数相乘,积是2004,求它们的和.
参考答案
一、单选题
1.【答案】
C
【解析】【解答】因为,11、13和17是质数,15是合数,
故答案为:C.
【分析】根据合数与质数的认识进行解答.
2.【答案】
A
【解析】【解答】解:符合要求的只有3+2=5,所以b=2.
故答案为:A
【分析】从最小的质数开始试算,直到确定出符合a+b=c的算式就可以确定b的值.
3.【答案】
B
【解析】【解答】解:两个质数相乘的积,除了1和它本身外,这两个数也是它的因数。
故答案为:B
【分析】除了1和它本身外,还有别的因数的数是合数。
4.【答案】
C
【解析】【解答】在2至12中质数有2、3、5、7、11,共5个。
故答案为:C
【分析】质数:一个大于1的自然数,除了1和它本身外,不再有其他的因数,这样的数就是质数。
二、判断题
5.【答案】
错误
【解析】【解答】例如0和1是相邻的两个数,但它们不是互质数,所以原题说法错误.
故答案为:错误
【分析】互质数的定义:只有公因数1的两个数是互质数.采用举例子的方法是解答判断题常用的方法.
6.【答案】正确
【解析】【解答】解:在非0自然数列中,除2以外,所有的偶数的因数除了1和它本身以外,一定还有因数2,所以除了2以外的非0偶数都是合数.原题说法正确.
故答案为:正确【分析】合数是除了1和本身外还有其它因数的数,最小的合数是4,大于4的所有偶数都是合数,但是合数也有奇数.
7.【答案】
错误
【解析】【解答】解:例如2是2的倍数,但2是质数,原题说法错误.
故答案为:错误
【分析】合数是除了1和本身外还有其它因数的数,除了0、2之外,所有的偶数都是合数.
三、填空题
8.【答案】
2
;3
;5
;7
【解析】【解答】解:
210=2×3×5×7
故答案为:2,3,5,7.
【分析】根据短除法写出210的质因数进行解答.
9.【答案】15
【解析】【解答】解:10以内以内的奇数中,所有的质数有:3,5,7.
所以:10以内所有的质数的和是:3+5+7=15.
故答案为:15.
【分析】写出10以内的所有质数,再相加即可.
10.【答案】
10
【解析】【解答】解:由于每个班至少1个名额,6﹣3=3.
在每班保证一个的情况,还剩三个名额:
共有3×1+3×2+1=10(种).
答:共有10种不同的分法.
故答案为:10.
【分析】由于每个班至少1个名额,所以,本题的分配方案实质上就是对余下3个名额的分配方案:
(1)把3个名额都给一个班级:3种;
(2)将3个名额分成1个和2个进行分配共3×2=6种分法;
(1)将3个名额分成1、1、1进行分配共1种分法.即平均每班两个名额.
所以共有3+6+1=10种分法.
11.【答案】
2
;合
【解析】【解答】如果一个非0自然数能被2整除,这个数就是偶数,不能被2整除,这个数就是合数;一个数只有两个约数,这个数就是合数,至少有3个约数,这个数就是合数.
故答案为:2;合
【分析】偶数都能被2整除,奇数都不能被2整除;质数是只有1和本身两个因数的数,合数是除了1和本身外还有其他因数的数.
12.【答案】101;93
【解析】【解答】解:100以内最大的质数与最小的合数的和是101和93.
故答案为:101;93.
【分析】本题考查的主要内容是质数和合数的应用问题,根据质数和合数的定义进行分析.
四、解答题
13.【答案】
解:方法一:“树枝”图式分解法.
①先把60分解成两个数相乘形式,60分解成2×30.
②2是质数,不需再分解;30是合数,需再进行分解;直到所有因数是质数为止.
③写出分解结果.合数后面写等号,然后把分解出的质数用连乘形式写在等号后.
分解过程如图所示:
60=2×3×2×5
也可以先把60分解成6×10或4×15,然后再依次分解.如图:
60=3×2×5×2
60=2×2×3×5
从60的分解过程可以看出,60的质因数是2、3、2、5这四个数,分解过程中只是2、2、3、5的顺序不同.
方法二:短除法分解质因数.
①把要分解的数60写在短除号里.
②用60的质因数去除,一般从最小的质因数开始.
③直到商是质数为止.
④把除数和商写成相乘形式.
分解过程如下:
60=2×3×2×5
分解方式不仅有以上一种,还有其他分解方式,也可以按如下方式分解:
60=3×5×2×2
60=5×3×2×2
60=3×2×5×2
【解析】【分析】本题考查的主要内容是质因数的应用问题,根据质因数的定义进行分析.
14.【答案】解:
【解析】【解答】2和3的最大公因数是1;3和4的最大公因数是1;3和6的最大公因数是3;3和8的最大公因数是1;3和1的最大公因数是1;3和12的最大公因数是3;6和2的最大公因数是2;6和4的最大公因数是2;6和6的最大公因数是6;6和8的最大公因数是2;6和10的最大公因数是2;6和12的最大公因数是6;8和2的最大公因数是2;8和4的最大公因数是4;8和6的最大公因数是2;8和8的最大公因数是8;8和10的最大公因数是2;8和12的最大公因数是4;9和2的最大公因数是1;9和4的最大公因数是1;9和6的最大公因数是3;9和8的最大公因数是1;9和10的最大公因数是1;9和12的最大公因数是3;15和2的最大公因数是1;15和4的最大公因数是1;15和6的最大公因数是3;15和8的最大公因数是1;15和10的最大公因数是5;15和12的最大公因数是3.
故答案为:
【分析】两个数的最大公因数就是两个数公有的质因数的积;互质数的两个数的最大公因数是1;相邻的两个数的最大公因数是1.
五、综合题
15.【答案】
(1)解:63=1×63,每个盒子里装一个,或者将63个球装在一个盒子里,
63=3×21,每个盒子里装3个或每个盒子里装21个,
63=7×9,每个盒子里装7个或每个盒子里装9个,
装法有:2+2+2=6(种),
答:有6种不同的装法
(2)解:67是质数,所以只有2种装法:每个盒子里装一个,或者将67个球装在一个盒子里.
答:有2种装法
【解析】【分析】(1)根据题意,即把63个求平均分到若干个盒子里,那么两个数相乘积是63,因为没有规定盒子的个数,所有63有多少个因数就有几种装法,列式解答即可得到答案.(2)67是质数,所以67=1×67,由此即可得出只有2种不同的装法.解答此题关键将63和67进行分解因数,有几个因数就有几种装法.
六、应用题
16.【答案】
解:2004=2×2×3×167=1×12×167,
所以A=1,B=12,C=167
这三个数的和为:1+12+167=180,
答:它们的和为180
【解析】【分析】先把2004分解质因数得出A、B、C的值再相加即可.本题主要考查了合数分解质因数,关键是得出A、B、C的值.
