一题可破万题山——二次函数压轴题常见模型小结(PDF版,无答案)
文档属性
| 名称 | 一题可破万题山——二次函数压轴题常见模型小结(PDF版,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览



文档简介
1
——二次函数压轴题常见模型小结
2
【特别说明】:
本次培训内容并非原创
根据王勇战老师《2019中考数学模型教学研讨会》分享内容学习整理
王勇战:郑州市名师,挑战压轴题郑州教研基地理事长。
编写有《冲刺十招》、《突围》、《春季攻势》、《沙场秋点兵》等书籍
D
B O
A
x
y
C
问题1:求抛物线解析式和顶点D坐标
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
1 2
( )( )y a x x x x? ? ?
2y ax bx c? ? ?
2( )y a x h k? ? ?
十字相乘
配方法(★)
1 2
轴交点( ,0)、( ,0)x x x
轴交点(0,c)y
顶点(h,k)
原始三角形:
重视四点围成的
三角形(边、角
关系)
函数 点 形
2
2
2 3
( 3)( 1)
( 1) 4
y x x
y x x
y x
? ? ?
? ? ?
? ? ?
3
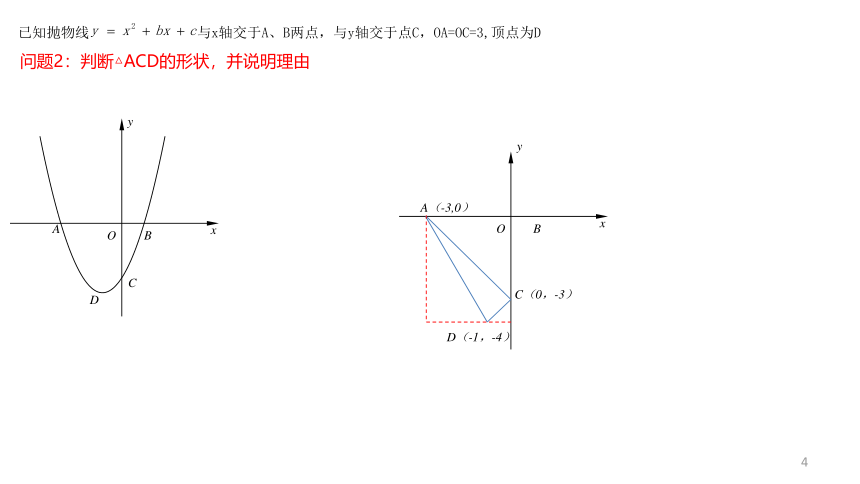
问题2:判断△ACD的形状,并说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
B O
A(-3,0)
x
y
C(0,-3)
4
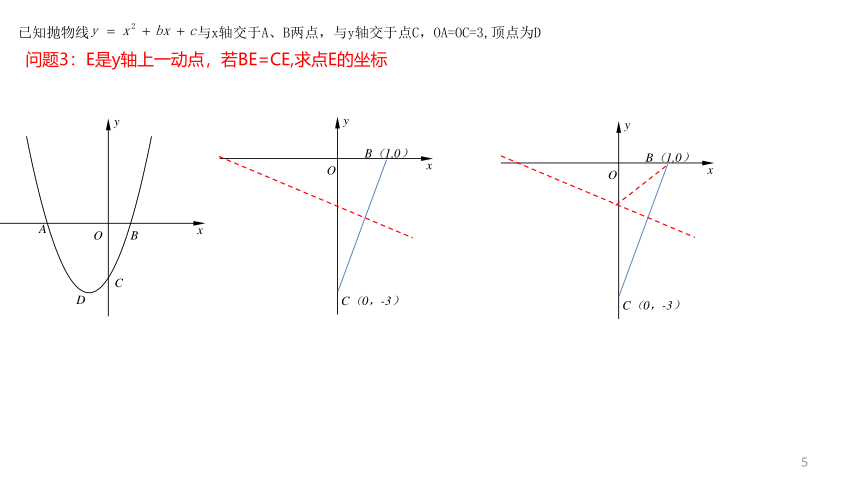
问题3:E是y轴上一动点,若BE=CE,求点E的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
x
y
C(0,-3)
B(1,0)
O
x
y
C(0,-3)
5
问题4:抛物线上有一动点P,过点P作PM⊥x轴于点M,交直线AC与点N,在线段PM、
MN中,若其中一条线段是另一条线段的2倍,求点P的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
6
问题5:直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,求线段PH的
最大值及此时点P的坐标
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C P
H
D
B O
A
x
y
C P
H
E
F
D
B O
A
x
y
C P
H
E
F
7
问题6:直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,PG∥y轴交AC
于G,PH为邻边作矩形PEGH,求矩形PEGH周长的最大值。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C P
H
E
G
8
问题7:在对称轴上找一点P,使得△BCP的周长最小,求出P点坐标及△BCP的周长
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
.x=1
P
9
问题8:在对称轴上找一点P,使得∣PA-PC∣最大,求出P点坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
.x=1
P
10
问题9:线段MN=1,在对称轴上运动(M点在N点上方),
求四边形BMNC周长的最小值及此时M点坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
.x=1
N
B’ B’’
M
11
将军饮马:这个将军饮的不是马,是数学!
解题依据:两点间线段最短;点到直线的垂直距离最短;翻折,对称。
解题策略:对称、翻折→化同为异;化异为同;化折为直。
· ·
A
B
P
两村一路(异侧)
和最小
两村一路(同侧)
和最小
一村两路和最小 两村两路和最小
两村一路(线段)和最小
两村一路(同侧)
差最大
两村一路(异侧)
差最大
12
问题10:求四边形ABCD的面积
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
E
D(-1,-4)
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
E F
13
问题11:在AC下方的抛物线上有一动点N,使得三角形CAN的面积最大?若存在,
请求出△CAN的最大面积及点N的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C N
E
F
14
宽高法(铅垂线法):S =(宽×高)÷2
★重点:什么是宽?什么是高?如何确定? (横平竖直;改斜归正)
定义:过三角形的一个顶点做y轴的平行线(x轴的垂线)与这个顶点的对边
(或延长线)相交,交点到这点的距离(纵坐标的差的绝对值)叫做该三角形
的“高”(竖直高);另外两个顶点的水平距离(横坐标的差的绝对值)叫做
该三角形的“宽”(水平宽)。具体操作时有如图所示的三种情形:
A
B
C
D
m
S=(m×AD)÷2
A
B
C
D
S=(m×CD)÷2
A
B
C
D
m
S=(m×BD)÷2
m
注:一般来讲:过动点(设横表纵)做y轴的平行线与其对边或延长线相交!
15
问题12:在AC下方的抛物线上有一动点N,使得四边形ABCN的面积最大?若存在,
请求出四边形ABCN的最大面积。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C N
E
F
16
问题13:抛物线上是否存在点N,使得S△ABN= S△ABC,若存在,求出点N的坐标;
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
N2
N1
N3
17
问题14:抛物线上是否存在点H,使得S△BCH= S△ABC,若存在,求出点H的坐标;
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O A
x
y
C
H
18
问题15:抛物线上是否存在点Q,使得S△AOQ= S△COQ,若存在,求出点Q的坐标;
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
Q1
Q2
19
问题16:抛物线上是否存在点E,使得BE平分△ABC的面积,若存在,求出E点坐标,
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
E
F
20
问题17:抛物线上找一点P,作PM⊥x轴,交线段AC于点N,使AC平分△APM的面积
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C P
M
N
21
问题18:抛物线上找一点P,作PM⊥x轴,交线段AC于点N,使AC分△APM的面
积为2:1两部分?
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B
O
A
x
y
C P
M
N
22
问题19:在y轴上是否存在一点E,使得△ADE是直角三角形?若存在,求出点E的
坐标;若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
O
x
y
A(-3,0)
D(-1,-4)
O
x
y
A(-3,0)
D(-1,-4)
O
x
y
A(-3,0)
E1
E2
E3
E4
23
问题20:在y轴上是否存在一点F,使得△ADF是等腰三角形?若存在,求出点F的坐
标;若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
O
x
y
A(-3,0)
F1
F2
F3
F4
F5
D(-1,-4)
O
x
y
A(-3,0)
F5
24
问题21:作垂直于x轴的直线x=-1交直线AC于点M,交抛物线于点N,以A、M、
N、E为顶点作平行四边形,求第四个顶点E的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
N
B O A
x
y
C
M
x=-1
25
问题22:在对称轴上有一点M,在抛物线上有一点N,若以A、B、M、N为顶点
的四边形为平行四边形,求M、N的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
D
B O A
x
y
C
26
平行四边形的存在性
预备知识:①中点坐标公式;②三平三交定三点;③两对角线端点的横、纵坐标
之和分别相等(秒杀必备);④横平竖直接做辅助。
分类
三定一动:用②③即可秒杀(本质还是中点坐标公式)
两定两动
两点之间线
段是一条边
两点之间线
段是对角线
利用①②③
④综合解决
27
问题23:点E是抛物线上一动点,点F在抛物线的对称轴上,若以C、D、E、F为顶
点的四边形为菱形,求点E的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B
O
A
x
y
C
x=-1
28
问题24:在线段AC上是否存在点M,使得三角形AOM与△ABC相似?若存在,
求出点M的坐标,若不能,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B O
A
x
y
C
B O
A
x
y
C
29
问题25:P是抛物线上一个动点,作PH⊥x轴于H,是否存在一点P,使得△PAH与
△BOC相似?若存在,求出点P的坐标,若不能,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
30
问题26:在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,求出点P的坐标,
若不能,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
31
问题27:过点B的直线交直线AC与点M,当直线AC与BM的夹角等于∠ACB的2倍时,
直接写出点M的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B
O
A
x
y
C
32
问题28:y轴上是否存在点N,使得∠BCO+ ∠BNO= ∠BAC?若存在,请写出点N的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B
O
A
x
y
C
33
问题29:将△BOC绕平面内一点顺时针转90°,得到△B’O’P’,若△B’O’P’
恰好有两个点同时落在抛物线上,求点O’的坐标?
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
D
B O
A
x
y
C
34
问题30:将AD所在的直线绕点A逆时针旋转45°,所得直线与抛物线交于点M,求M点坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
35
题号 针对变式题目
形定问题 1-解析式、2-三角形形状
线段问题 3-线段相等、4-线段成比例
最值问题 5-线段最值1(直)、 6-线段最值2(斜) 、 7-和最小
8-差最大 、 9-两村一路
面积问题 10-定点求面积 、11-斜三角形求面积 、 12-(定+动)求面积
13-同底等高(直)、14-同底等高(斜)、15-面积平分1
16-面积平分 2 、17-面积平分3 、 18-面积分割
特殊图形 19-直角三角形 、20-等腰三角形 、21-平行四边形1
22-平行四边形2 、23-菱形 、 24-相似三角形1
25-相似三角形2
角度问题 26-角相等 、27-倍半角、28-和差角
旋转问题 29-形旋转 、30-线旋转
…… ……
——二次函数压轴题常见模型小结
2
【特别说明】:
本次培训内容并非原创
根据王勇战老师《2019中考数学模型教学研讨会》分享内容学习整理
王勇战:郑州市名师,挑战压轴题郑州教研基地理事长。
编写有《冲刺十招》、《突围》、《春季攻势》、《沙场秋点兵》等书籍
D
B O
A
x
y
C
问题1:求抛物线解析式和顶点D坐标
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
1 2
( )( )y a x x x x? ? ?
2y ax bx c? ? ?
2( )y a x h k? ? ?
十字相乘
配方法(★)
1 2
轴交点( ,0)、( ,0)x x x
轴交点(0,c)y
顶点(h,k)
原始三角形:
重视四点围成的
三角形(边、角
关系)
函数 点 形
2
2
2 3
( 3)( 1)
( 1) 4
y x x
y x x
y x
? ? ?
? ? ?
? ? ?
3
问题2:判断△ACD的形状,并说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
B O
A(-3,0)
x
y
C(0,-3)
4
问题3:E是y轴上一动点,若BE=CE,求点E的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
x
y
C(0,-3)
B(1,0)
O
x
y
C(0,-3)
5
问题4:抛物线上有一动点P,过点P作PM⊥x轴于点M,交直线AC与点N,在线段PM、
MN中,若其中一条线段是另一条线段的2倍,求点P的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
6
问题5:直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,求线段PH的
最大值及此时点P的坐标
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C P
H
D
B O
A
x
y
C P
H
E
F
D
B O
A
x
y
C P
H
E
F
7
问题6:直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,PG∥y轴交AC
于G,PH为邻边作矩形PEGH,求矩形PEGH周长的最大值。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C P
H
E
G
8
问题7:在对称轴上找一点P,使得△BCP的周长最小,求出P点坐标及△BCP的周长
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
.x=1
P
9
问题8:在对称轴上找一点P,使得∣PA-PC∣最大,求出P点坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
.x=1
P
10
问题9:线段MN=1,在对称轴上运动(M点在N点上方),
求四边形BMNC周长的最小值及此时M点坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
.x=1
N
B’ B’’
M
11
将军饮马:这个将军饮的不是马,是数学!
解题依据:两点间线段最短;点到直线的垂直距离最短;翻折,对称。
解题策略:对称、翻折→化同为异;化异为同;化折为直。
· ·
A
B
P
两村一路(异侧)
和最小
两村一路(同侧)
和最小
一村两路和最小 两村两路和最小
两村一路(线段)和最小
两村一路(同侧)
差最大
两村一路(异侧)
差最大
12
问题10:求四边形ABCD的面积
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
E
D(-1,-4)
B(1,0)
O
A(-3,0)
x
y
C(0,-3)
E F
13
问题11:在AC下方的抛物线上有一动点N,使得三角形CAN的面积最大?若存在,
请求出△CAN的最大面积及点N的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C N
E
F
14
宽高法(铅垂线法):S =(宽×高)÷2
★重点:什么是宽?什么是高?如何确定? (横平竖直;改斜归正)
定义:过三角形的一个顶点做y轴的平行线(x轴的垂线)与这个顶点的对边
(或延长线)相交,交点到这点的距离(纵坐标的差的绝对值)叫做该三角形
的“高”(竖直高);另外两个顶点的水平距离(横坐标的差的绝对值)叫做
该三角形的“宽”(水平宽)。具体操作时有如图所示的三种情形:
A
B
C
D
m
S=(m×AD)÷2
A
B
C
D
S=(m×CD)÷2
A
B
C
D
m
S=(m×BD)÷2
m
注:一般来讲:过动点(设横表纵)做y轴的平行线与其对边或延长线相交!
15
问题12:在AC下方的抛物线上有一动点N,使得四边形ABCN的面积最大?若存在,
请求出四边形ABCN的最大面积。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C N
E
F
16
问题13:抛物线上是否存在点N,使得S△ABN= S△ABC,若存在,求出点N的坐标;
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
N2
N1
N3
17
问题14:抛物线上是否存在点H,使得S△BCH= S△ABC,若存在,求出点H的坐标;
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O A
x
y
C
H
18
问题15:抛物线上是否存在点Q,使得S△AOQ= S△COQ,若存在,求出点Q的坐标;
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
Q1
Q2
19
问题16:抛物线上是否存在点E,使得BE平分△ABC的面积,若存在,求出E点坐标,
若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
E
F
20
问题17:抛物线上找一点P,作PM⊥x轴,交线段AC于点N,使AC平分△APM的面积
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C P
M
N
21
问题18:抛物线上找一点P,作PM⊥x轴,交线段AC于点N,使AC分△APM的面
积为2:1两部分?
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B
O
A
x
y
C P
M
N
22
问题19:在y轴上是否存在一点E,使得△ADE是直角三角形?若存在,求出点E的
坐标;若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
O
x
y
A(-3,0)
D(-1,-4)
O
x
y
A(-3,0)
D(-1,-4)
O
x
y
A(-3,0)
E1
E2
E3
E4
23
问题20:在y轴上是否存在一点F,使得△ADF是等腰三角形?若存在,求出点F的坐
标;若不存在,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D(-1,-4)
O
x
y
A(-3,0)
F1
F2
F3
F4
F5
D(-1,-4)
O
x
y
A(-3,0)
F5
24
问题21:作垂直于x轴的直线x=-1交直线AC于点M,交抛物线于点N,以A、M、
N、E为顶点作平行四边形,求第四个顶点E的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
N
B O A
x
y
C
M
x=-1
25
问题22:在对称轴上有一点M,在抛物线上有一点N,若以A、B、M、N为顶点
的四边形为平行四边形,求M、N的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
D
B O A
x
y
C
26
平行四边形的存在性
预备知识:①中点坐标公式;②三平三交定三点;③两对角线端点的横、纵坐标
之和分别相等(秒杀必备);④横平竖直接做辅助。
分类
三定一动:用②③即可秒杀(本质还是中点坐标公式)
两定两动
两点之间线
段是一条边
两点之间线
段是对角线
利用①②③
④综合解决
27
问题23:点E是抛物线上一动点,点F在抛物线的对称轴上,若以C、D、E、F为顶
点的四边形为菱形,求点E的坐标
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B
O
A
x
y
C
x=-1
28
问题24:在线段AC上是否存在点M,使得三角形AOM与△ABC相似?若存在,
求出点M的坐标,若不能,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B O
A
x
y
C
B O
A
x
y
C
29
问题25:P是抛物线上一个动点,作PH⊥x轴于H,是否存在一点P,使得△PAH与
△BOC相似?若存在,求出点P的坐标,若不能,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
30
问题26:在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,求出点P的坐标,
若不能,请说明理由
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
31
问题27:过点B的直线交直线AC与点M,当直线AC与BM的夹角等于∠ACB的2倍时,
直接写出点M的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B
O
A
x
y
C
32
问题28:y轴上是否存在点N,使得∠BCO+ ∠BNO= ∠BAC?若存在,请写出点N的坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
B
O
A
x
y
C
33
问题29:将△BOC绕平面内一点顺时针转90°,得到△B’O’P’,若△B’O’P’
恰好有两个点同时落在抛物线上,求点O’的坐标?
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
D
B O
A
x
y
C
34
问题30:将AD所在的直线绕点A逆时针旋转45°,所得直线与抛物线交于点M,求M点坐标。
D
B O
A
x
y
C
已知抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D
2y x bx c? ? ?
D
B O
A
x
y
C
35
题号 针对变式题目
形定问题 1-解析式、2-三角形形状
线段问题 3-线段相等、4-线段成比例
最值问题 5-线段最值1(直)、 6-线段最值2(斜) 、 7-和最小
8-差最大 、 9-两村一路
面积问题 10-定点求面积 、11-斜三角形求面积 、 12-(定+动)求面积
13-同底等高(直)、14-同底等高(斜)、15-面积平分1
16-面积平分 2 、17-面积平分3 、 18-面积分割
特殊图形 19-直角三角形 、20-等腰三角形 、21-平行四边形1
22-平行四边形2 、23-菱形 、 24-相似三角形1
25-相似三角形2
角度问题 26-角相等 、27-倍半角、28-和差角
旋转问题 29-形旋转 、30-线旋转
…… ……
同课章节目录
