人教版八年级数学下册17.1 勾股定理课件 (第1课时,区级示范课,共25张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.1 勾股定理课件 (第1课时,区级示范课,共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 17:05:17 | ||
图片预览






文档简介
(共25张PPT)
17.1 勾股定理
第十七章 勾股定理
第1课时 勾股定理
1、 经历勾股定理的探究过程,了解关于勾股定理的
一些文化历史背景,通过对于我国古代研究勾股
定理的成就的介绍,培养学生的民族自豪感;
2、能用勾股定理解决一些简单问题 .
其他星球上是否存在着“人”呢?为了探寻这一点,世界上许多科学家向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等.
情景引入
据说我国著名的数学家华罗庚曾建议“发射”一种勾股定理的图形(如图).
很多学者认为如果宇宙“人”也拥有文明的话,那么他们一定会认识这种语言,因为几乎所有具有古代文化的民族和国家都对勾股定理有所了解.
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
问题1 试问正方形A、B、C面积之间有什么样的数量关系?
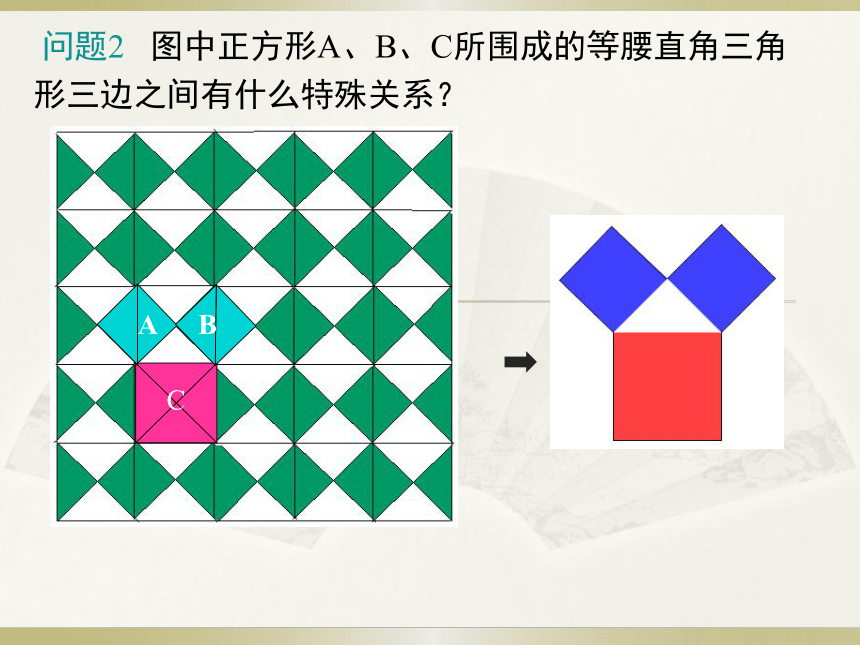
问题2 图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系?
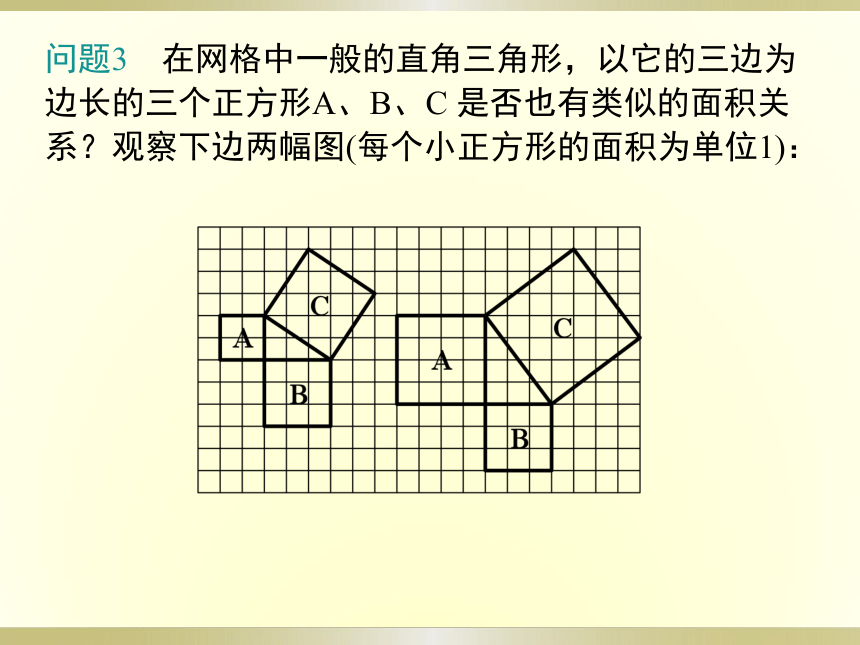
问题3 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
问题4:正方形A、B、C 所围成的直角三角形三条边之
间有怎样的特殊关系?
猜想: 如果直角三角形的两条直角边长分别为a,b,斜
边长为c,那么a2+b2=c2.两直角边的平方和等于
斜边的平方.
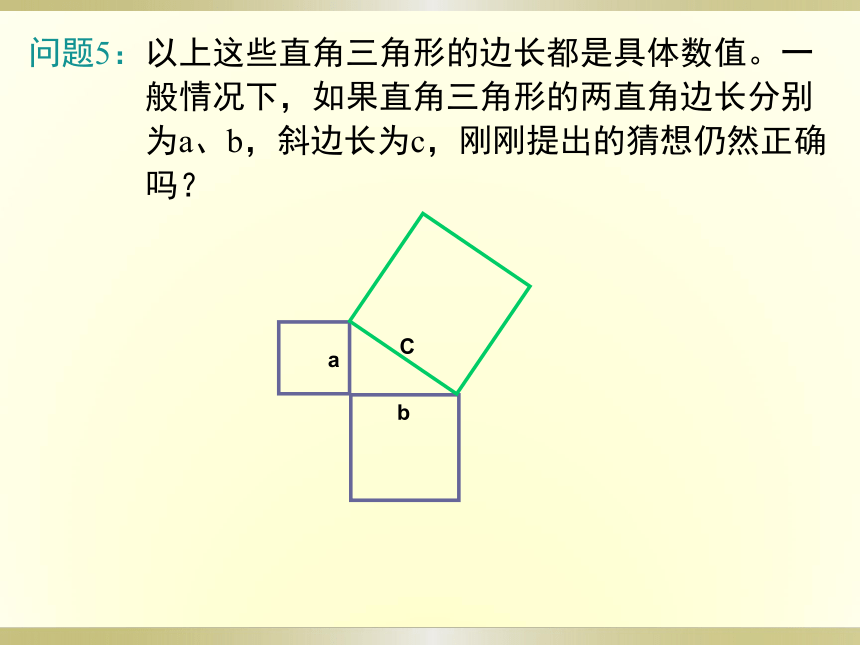
问题5:以上这些直角三角形的边长都是具体数值。一
般情况下,如果直角三角形的两直角边长分别
为a、b,斜边长为c,刚刚提出的猜想仍然正确
吗?
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
a
b
b
c
a
b
c
a
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
归纳总结
3
4
5
∟
勾
股
弦
公元前1100年
古希腊著名数学家
赵爽----东汉末至三国时代吴国人
美国第二十任总统伽菲尔德
总统证明法
a2 + b2 = c2.
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
(2)据勾股定理得
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
【变式题1】在Rt△ABC中, ∠C=90°.
x2+(2x)2=52,
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
【变式题2】 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图?,
当BC为斜边时,如图?,
图?
图?
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
例2:如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
解:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB= .
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD= ,∴BC=BD+CD=1+ ,
∴△ABC的周长=AB+AC+BC= .
3、小明妈妈买了一部29英寸(74厘米)的电视机。
小明量了电视机的屏幕后,发现屏幕只有58厘
米长和46厘米宽,他觉得一定是售货员搞错了。
你同意他的想法吗?你能解释这是为什么吗?
解:∵AE=BE,
∴S△ABE= AE·BE= AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE= AB2= ;
同理可得S△AHC+S△BCF= AC2+ BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为 AB2= .
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
能力提升:
课堂小结
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
17.1 勾股定理
第十七章 勾股定理
第1课时 勾股定理
1、 经历勾股定理的探究过程,了解关于勾股定理的
一些文化历史背景,通过对于我国古代研究勾股
定理的成就的介绍,培养学生的民族自豪感;
2、能用勾股定理解决一些简单问题 .
其他星球上是否存在着“人”呢?为了探寻这一点,世界上许多科学家向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等.
情景引入
据说我国著名的数学家华罗庚曾建议“发射”一种勾股定理的图形(如图).
很多学者认为如果宇宙“人”也拥有文明的话,那么他们一定会认识这种语言,因为几乎所有具有古代文化的民族和国家都对勾股定理有所了解.
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
问题1 试问正方形A、B、C面积之间有什么样的数量关系?
问题2 图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系?
问题3 在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
问题4:正方形A、B、C 所围成的直角三角形三条边之
间有怎样的特殊关系?
猜想: 如果直角三角形的两条直角边长分别为a,b,斜
边长为c,那么a2+b2=c2.两直角边的平方和等于
斜边的平方.
问题5:以上这些直角三角形的边长都是具体数值。一
般情况下,如果直角三角形的两直角边长分别
为a、b,斜边长为c,刚刚提出的猜想仍然正确
吗?
下面动图形象的说明命题1的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想.
a
b
b
c
a
b
c
a
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
归纳总结
3
4
5
∟
勾
股
弦
公元前1100年
古希腊著名数学家
赵爽----东汉末至三国时代吴国人
美国第二十任总统伽菲尔德
总统证明法
a2 + b2 = c2.
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
(2)据勾股定理得
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
【变式题1】在Rt△ABC中, ∠C=90°.
x2+(2x)2=52,
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
【变式题2】 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图?,
当BC为斜边时,如图?,
图?
图?
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
例2:如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
解:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB= .
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD= ,∴BC=BD+CD=1+ ,
∴△ABC的周长=AB+AC+BC= .
3、小明妈妈买了一部29英寸(74厘米)的电视机。
小明量了电视机的屏幕后,发现屏幕只有58厘
米长和46厘米宽,他觉得一定是售货员搞错了。
你同意他的想法吗?你能解释这是为什么吗?
解:∵AE=BE,
∴S△ABE= AE·BE= AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE= AB2= ;
同理可得S△AHC+S△BCF= AC2+ BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为 AB2= .
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
能力提升:
课堂小结
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
