人教版九年级数学 下册 26.1.2 反比例函数的图像和性质 课件(共24张PPT)
文档属性
| 名称 | 人教版九年级数学 下册 26.1.2 反比例函数的图像和性质 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 793.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 14:38:02 | ||
图片预览







文档简介
(共24张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
26.1.2 反比例函数的图象与性质
人教版八年级数学 下册
目标导航
1.会画反比例函数的图象。
2.理解反比例函数图象的性质。
3、能够运用反比例函数的性质解决简单的实际问题。
2. 已知函数 是正比例函数,则 m = ___ ;
已知函数 是反比例函数,则 m = ___ 。
4
5
1.什么是反比例函数?
一般地,形如 y = — ( k是常数, k ≠ 0 ) 的函数叫做反比例函数。
k
x
知识回顾
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象(graph)
回顾:一次函数y=2x+1的图象的作法过程:
解:列表:
x … -2 -1 0 1 2 …
y=2x+1 … …
-3
-1
1
3
5
知识回顾
y
x
-1
-1
0
1
1
3
2
5
-2
-3
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
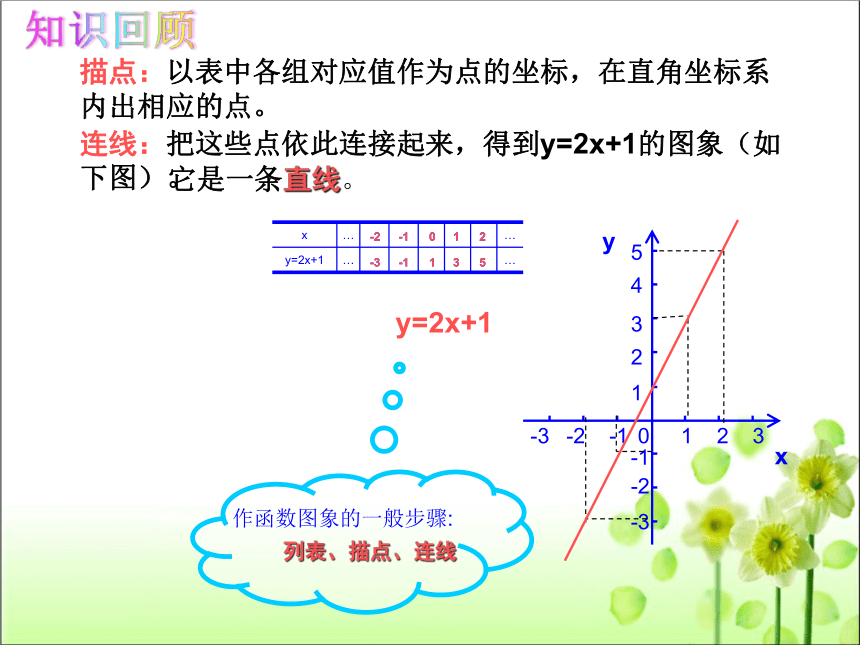
描点:以表中各组对应值作为点的坐标,在直角坐标系内出相应的点。
连线:把这些点依此连接起来,得到y=2x+1的图象(如下图)。
作函数图象的一般步骤:
列表、描点、连线
y=2x+1
x … …
y=2x+1 … …
-2
-3
-1
-1
0
1
1
3
2
5
它是一条直线。
知识回顾
认真阅读课本26.1.2反比例函数的图象与性质部分内容,完成下面练习并体验知识点的形成过程。
自主研学
例.画出函数 y = — 的图象。
4
x
思考:
(1)这个函数中自变量的取值范围是什么?
(2)画函数图象的三个步骤是什么?
因为分母不能为零,所以 x = 0。
列表、描点、连线。
解:
列表:
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
1
2
4
8
-8
-4
-2
-1
合作探究
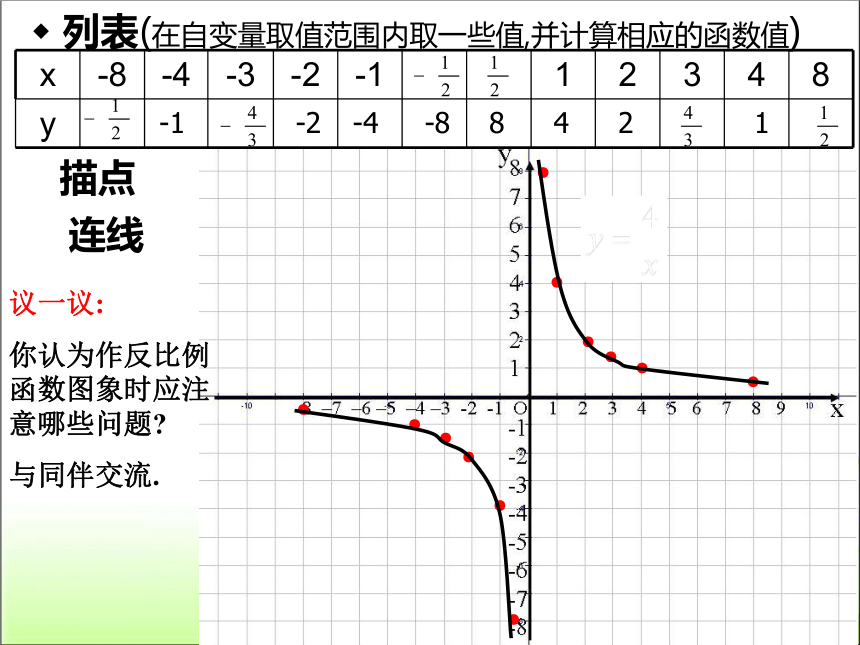
列表(在自变量取值范围内取一些值,并计算相应的函数值)
连线
描点
x -8 -4 -3 -2 -1 1 2 3 4 8
y
-1
-2
-4
-8
8
4
2
1
●
●
●
●
●
●
●
●
●
●
●
●
议一议:
你认为作反比例函数图象时应注意哪些问题?
与同伴交流.
作反比例函数图象时应注意以下问题:
1.在列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点.
2.列表、描点时,要尽量多取一些点,这样方便连线.
4.连线时必须用光滑的曲线连接各点;
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
3.描点时一定要养成按自变量从小到大的顺序依次画线, 从中体会函数的增减性;
合作探究
画出函数 y =-— 的图象
4
x
解:
列表:
描点:
连线:
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
-1
-2
-4
-8
8
4
2
1
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
用光滑的曲线顺次连接各点,就可得到
的图象.
即学即练
.
-1
-2
-4
-8
8
4
2
1
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
…
…
.
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
y
x
y =- —
4
x
.
.
.
.
.
y
-6
-6
y
6
-6
-5
x
1
2
3
4
5
-4
-1
-2
-3
1
2
4
5
6
3
-5
-1
-3
-4
-2
0
x
合作探究
反比例函数的图象和性质
形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内。
合作探究
在同一坐标系内作出函数 与函数y=x-1的图象,并利用图像求它们的交点坐标.
●
●
y=x-1
●
●
●
●
●
●
●
●
●
●
(-1,-2)
(2,1)
拓展提升
函数来自现实生活,函数是描述现实世界变化规律的重要数学模型。
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段。
课堂小结
反比例函数 y = — 有下列性质:
k
x
反比例函数的图象 是由两支曲线组成的。
(1) 当 k>0 时,两支曲线分别位于第___、___象限,
一
三
(2) 当 k<0 时,两支曲线分别位于第___、___象限.
二
四
x
y
y
x
0
(3) 反比例函数图象——与坐标轴不相交。
课堂小结
“双胞胎”之间的差异
x
y
o
x
y
o
检测目标
由k<0可知,两个函数的图象在第二,四象限,故可选(2),(4);再由y=k(x-1)=kx-k得-k>0,即一次函数与y轴的正半轴相交,因此选(2).
x
y
o
x
y
o
x
y
o
x
y
o
(1) (2) (3) (4)
检测目标
提高从函数的图象中获取信息的能力
x
y
o
x
y
o
说一说,当你看到下面的图象时,你能从中知道些什么?
x
y
o
x
y
o
x
y
o
y=kx+b
y=kx+b
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
26.1.2 反比例函数的图象与性质
人教版八年级数学 下册
目标导航
1.会画反比例函数的图象。
2.理解反比例函数图象的性质。
3、能够运用反比例函数的性质解决简单的实际问题。
2. 已知函数 是正比例函数,则 m = ___ ;
已知函数 是反比例函数,则 m = ___ 。
4
5
1.什么是反比例函数?
一般地,形如 y = — ( k是常数, k ≠ 0 ) 的函数叫做反比例函数。
k
x
知识回顾
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象(graph)
回顾:一次函数y=2x+1的图象的作法过程:
解:列表:
x … -2 -1 0 1 2 …
y=2x+1 … …
-3
-1
1
3
5
知识回顾
y
x
-1
-1
0
1
1
3
2
5
-2
-3
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
描点:以表中各组对应值作为点的坐标,在直角坐标系内出相应的点。
连线:把这些点依此连接起来,得到y=2x+1的图象(如下图)。
作函数图象的一般步骤:
列表、描点、连线
y=2x+1
x … …
y=2x+1 … …
-2
-3
-1
-1
0
1
1
3
2
5
它是一条直线。
知识回顾
认真阅读课本26.1.2反比例函数的图象与性质部分内容,完成下面练习并体验知识点的形成过程。
自主研学
例.画出函数 y = — 的图象。
4
x
思考:
(1)这个函数中自变量的取值范围是什么?
(2)画函数图象的三个步骤是什么?
因为分母不能为零,所以 x = 0。
列表、描点、连线。
解:
列表:
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
1
2
4
8
-8
-4
-2
-1
合作探究
列表(在自变量取值范围内取一些值,并计算相应的函数值)
连线
描点
x -8 -4 -3 -2 -1 1 2 3 4 8
y
-1
-2
-4
-8
8
4
2
1
●
●
●
●
●
●
●
●
●
●
●
●
议一议:
你认为作反比例函数图象时应注意哪些问题?
与同伴交流.
作反比例函数图象时应注意以下问题:
1.在列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点.
2.列表、描点时,要尽量多取一些点,这样方便连线.
4.连线时必须用光滑的曲线连接各点;
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
3.描点时一定要养成按自变量从小到大的顺序依次画线, 从中体会函数的增减性;
合作探究
画出函数 y =-— 的图象
4
x
解:
列表:
描点:
连线:
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
-1
-2
-4
-8
8
4
2
1
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
用光滑的曲线顺次连接各点,就可得到
的图象.
即学即练
.
-1
-2
-4
-8
8
4
2
1
x … -8 -4 -3 -2 -1 … 1 2 3 4 8
… …
…
…
.
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
y
x
y =- —
4
x
.
.
.
.
.
y
-6
-6
y
6
-6
-5
x
1
2
3
4
5
-4
-1
-2
-3
1
2
4
5
6
3
-5
-1
-3
-4
-2
0
x
合作探究
反比例函数的图象和性质
形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内。
合作探究
在同一坐标系内作出函数 与函数y=x-1的图象,并利用图像求它们的交点坐标.
●
●
y=x-1
●
●
●
●
●
●
●
●
●
●
(-1,-2)
(2,1)
拓展提升
函数来自现实生活,函数是描述现实世界变化规律的重要数学模型。
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段。
课堂小结
反比例函数 y = — 有下列性质:
k
x
反比例函数的图象 是由两支曲线组成的。
(1) 当 k>0 时,两支曲线分别位于第___、___象限,
一
三
(2) 当 k<0 时,两支曲线分别位于第___、___象限.
二
四
x
y
y
x
0
(3) 反比例函数图象——与坐标轴不相交。
课堂小结
“双胞胎”之间的差异
x
y
o
x
y
o
检测目标
由k<0可知,两个函数的图象在第二,四象限,故可选(2),(4);再由y=k(x-1)=kx-k得-k>0,即一次函数与y轴的正半轴相交,因此选(2).
x
y
o
x
y
o
x
y
o
x
y
o
(1) (2) (3) (4)
检测目标
提高从函数的图象中获取信息的能力
x
y
o
x
y
o
说一说,当你看到下面的图象时,你能从中知道些什么?
x
y
o
x
y
o
x
y
o
y=kx+b
y=kx+b
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
