湘教版八年级数学下册课件2.2.2.1平行四边形的判定定理1和2(15张)
文档属性
| 名称 | 湘教版八年级数学下册课件2.2.2.1平行四边形的判定定理1和2(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览






文档简介
课件15张PPT。第二章
四边形八年级数学湘教版·下册2.2.2.1 平行四边形的判定定理1、2学习目标
1.运用类比的方法,探索平行四边形的判定方法;
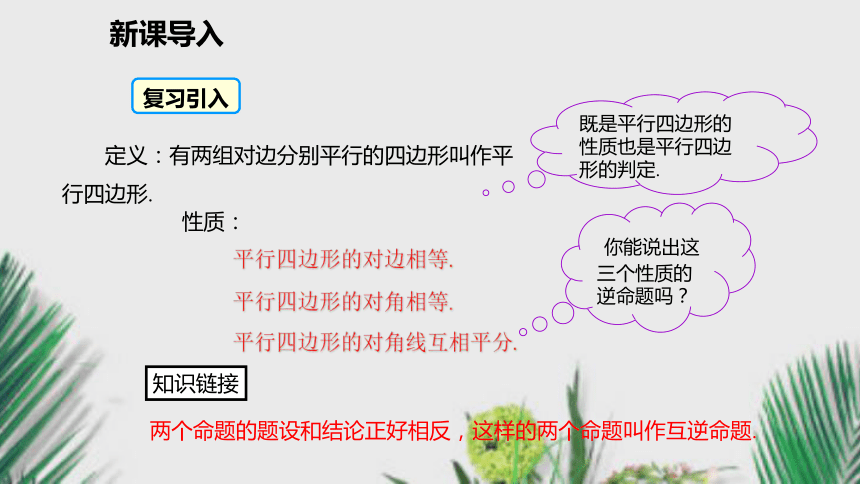
2.理解平行四边形的判定方法,并会简单运用;新课导入 定义:有两组对边分别平行的四边形叫作平行四边形.平行四边形的对边相等.平行四边形的对角相等.平行四边形的对角线互相平分.既是平行四边形的性质也是平行四边形的判定. 你能说出这三个性质的逆命题吗?知识链接两个命题的题设和结论正好相反,这样的两个命题叫作互逆命题.复习引入 性质:新知探究 通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分,那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢? 你能根据平行四边形的定义证明它们吗?新知探究作对角线构造全等三角形两组对应角相等两组对边分别平行四边形ABCD是平行四边形一组对边平行且相等的四边形是平行四边形.问题:已知:四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.新知探究连接AC .
∵AB∥CD, ∴∠2=∠3 .
在△ABC和△CDA中,AB=CD (已知),AC=CA(公共边),∠3=∠2,∴△ABC ≌△CDA(SAS),∴ ∠1=∠4, 又 ∠ 2=∠3,∴AB∥CD , AD∥BC ,∴四边形ABCD是平行四边形.新知探究例1 如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形. 证明:∵在平行四边形ABCD中,
AE,CF分别是∠DAB, ∠BCD的角平分线,
∴∠B=∠D,AB=CD,
∠BAE=∠DCF= ∠DAB= ∠BCD,新知探究∴△ABE ≌△CDF(ASA) ,
∴BE=DF, ∴AF=CE .
∵AF∥CE,
∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形).新知探究证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC,
∴AD BC,
∴四边形ABCD是平行四边形.例2 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.新知探究两组对边分别相等的四边形是平行四边形.问题:已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形.作对角线构造全等三角形两组对应角相等两组对边分别平行四边形ABCD是平行四边形新知探究连结AC,在△ABC和△CDA中,AB=CD (已知),BC=DA(已知),AC=CA (公共边),∴△ABC ≌△CDA(SSS),∴ ∠1=∠4 , ∠ 2=∠3,∴AB∥CD , AD∥BC,∴四边形ABCD是平行四边形.新知探究例3 如图,在平行四边形ABCD中,E,F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形.解:可求得△ABE ≌△CDF(SAS),
∴AE=CF.
又∵AF=CE,
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形).
课堂小结平行四边形的判定方法:定义法:两组对边分别平行的四边形是平行四边形.判定定理1 一组对边平行且相等的四边形是平行四边形.判定定理2 两组对边分别相等的四边形是平行四边形.知识要点课堂小测证明: ∵四边形ABCD是平行四边形,∴AD∥ BC且AD =BC,∠EAD = ∠FCB.∴△AED ≌△CFB(SAS),∴DE=BF.∴四边形BFDE是平行四边形.在△AED和△CFB中,同理可证:BE=DF,1.已知:E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.课堂小测2.已知:如图,E,F分别是 平行四边形ABCD 的边AD,BC的中点.
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD ,AD=BC,∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).∴BE=DF(平行四边形的对边分别相等).
1.运用类比的方法,探索平行四边形的判定方法;
2.理解平行四边形的判定方法,并会简单运用;新课导入 定义:有两组对边分别平行的四边形叫作平行四边形.平行四边形的对边相等.平行四边形的对角相等.平行四边形的对角线互相平分.既是平行四边形的性质也是平行四边形的判定. 你能说出这三个性质的逆命题吗?知识链接两个命题的题设和结论正好相反,这样的两个命题叫作互逆命题.复习引入 性质:新知探究 通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分,那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢? 你能根据平行四边形的定义证明它们吗?新知探究作对角线构造全等三角形两组对应角相等两组对边分别平行四边形ABCD是平行四边形一组对边平行且相等的四边形是平行四边形.问题:已知:四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.新知探究连接AC .
∵AB∥CD, ∴∠2=∠3 .
在△ABC和△CDA中,AB=CD (已知),AC=CA(公共边),∠3=∠2,∴△ABC ≌△CDA(SAS),∴ ∠1=∠4, 又 ∠ 2=∠3,∴AB∥CD , AD∥BC ,∴四边形ABCD是平行四边形.新知探究例1 如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形. 证明:∵在平行四边形ABCD中,
AE,CF分别是∠DAB, ∠BCD的角平分线,
∴∠B=∠D,AB=CD,
∠BAE=∠DCF= ∠DAB= ∠BCD,新知探究∴△ABE ≌△CDF(ASA) ,
∴BE=DF, ∴AF=CE .
∵AF∥CE,
∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形).新知探究证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC,
∴AD BC,
∴四边形ABCD是平行四边形.例2 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.新知探究两组对边分别相等的四边形是平行四边形.问题:已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形.作对角线构造全等三角形两组对应角相等两组对边分别平行四边形ABCD是平行四边形新知探究连结AC,在△ABC和△CDA中,AB=CD (已知),BC=DA(已知),AC=CA (公共边),∴△ABC ≌△CDA(SSS),∴ ∠1=∠4 , ∠ 2=∠3,∴AB∥CD , AD∥BC,∴四边形ABCD是平行四边形.新知探究例3 如图,在平行四边形ABCD中,E,F分别是边BC和AD上的两点,且AF=CE.
求证:四边形AECF为平行四边形.解:可求得△ABE ≌△CDF(SAS),
∴AE=CF.
又∵AF=CE,
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形).
课堂小结平行四边形的判定方法:定义法:两组对边分别平行的四边形是平行四边形.判定定理1 一组对边平行且相等的四边形是平行四边形.判定定理2 两组对边分别相等的四边形是平行四边形.知识要点课堂小测证明: ∵四边形ABCD是平行四边形,∴AD∥ BC且AD =BC,∠EAD = ∠FCB.∴△AED ≌△CFB(SAS),∴DE=BF.∴四边形BFDE是平行四边形.在△AED和△CFB中,同理可证:BE=DF,1.已知:E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.课堂小测2.已知:如图,E,F分别是 平行四边形ABCD 的边AD,BC的中点.
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD ,AD=BC,∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).∴BE=DF(平行四边形的对边分别相等).
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
