人教版九年级数学 下册 27.2.1 相似三角形的判定课件(共22张PPT)
文档属性
| 名称 | 人教版九年级数学 下册 27.2.1 相似三角形的判定课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 15:18:22 | ||
图片预览






文档简介
(共22张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
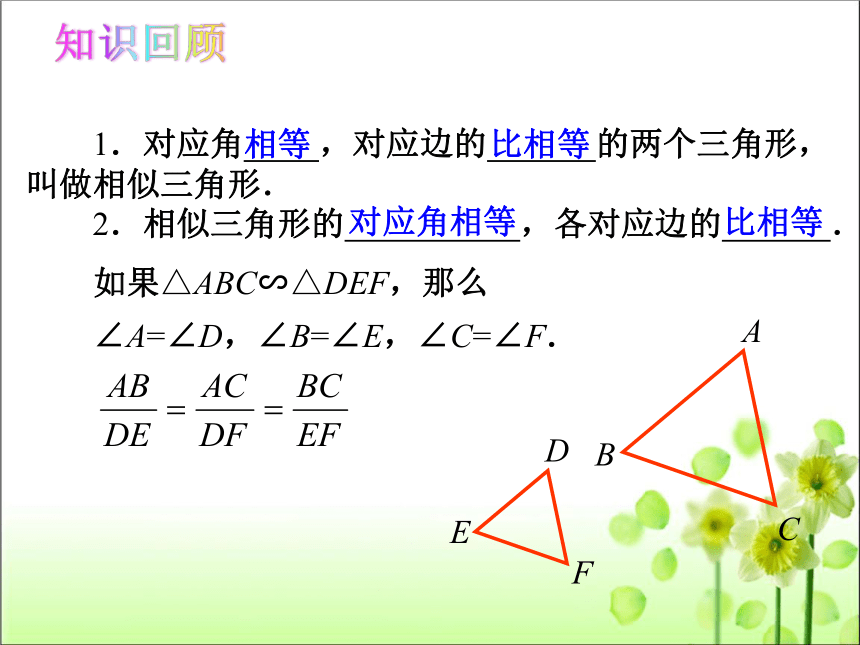
1.对应角 ,对应边的 的两个三角形,叫做相似三角形.
相等
比相等
对应角相等
比相等
∠A=∠D,∠B=∠E,∠C=∠F.
如果△ABC∽△DEF,那么
2.相似三角形的 ,各对应边的 .
学习三角形全等时,我们知道,除了可以验证所有的角和边分别相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
27.2.1 相似三角形的判定
人教版八年级数学 下册
1.掌握相似三角形的判定定理.
2.综合运用相似三角形的判定定理来解决问题.
3.进一步体验类比的学习思想.
请同学们阅读教材27.2.1 相似三角形的判定部分,理解并掌握其基本内容,初步归纳相似三角形的判定方法。
即对应角相等,对应边成比例,我们说△ABC与△DEF
相似,记作△ABC∽△DEF,△ABC 和△DEF的相似比
为 k, △DEF 与△ABC 的相似比为 .
∠A=∠D,∠B=∠E,∠C=∠F, ,
为了证明相似三角形的判定定理,我们先来学习下面的平行线分线段成比例这个基本事实.
定义:在△ABC 和△DEF中,如果
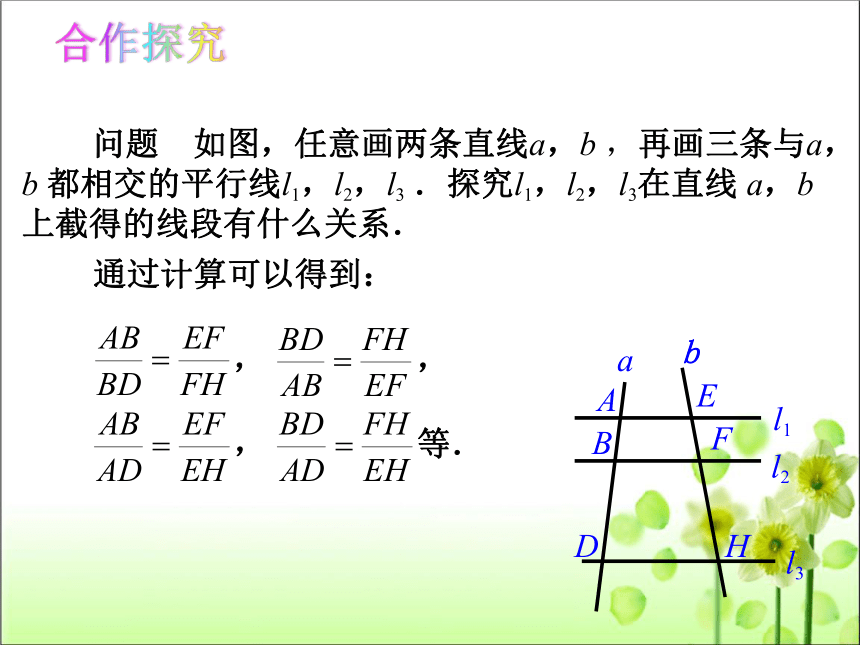
问题 如图,任意画两条直线a,b ,再画三条与a,b 都相交的平行线l1,l2,l3 .探究l1,l2,l3在直线 a,b 上截得的线段有什么关系.
通过计算可以得到:
等.
,
,
,
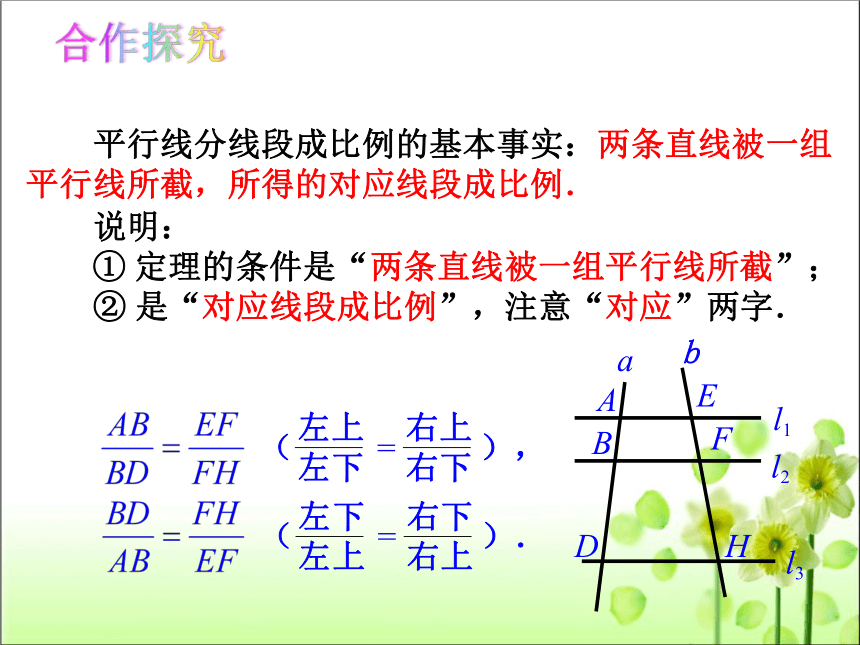
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
说明:
① 定理的条件是“两条直线被一组平行线所截”;
② 是“对应线段成比例”,注意“对应”两字.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
用定义证明△ADE∽△ABC, 需要具备的条件:
角:∠A=∠A,∠ADE=∠B,∠AED=∠C;
A
B
C
D
E
判定三角形相似的定理:
边: .
F
如何证明呢?
问题: 成立吗?
如图 l1∥l2∥l3,试根据图形写出成比例线段.
.
,
,
,
,
,
判定方法:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
问题2:在△ABC 与△ 中,如果满足∠B= ∠B',∠C=∠C',那么能否判定这两个三角形相似?
判定方法:两角分别相等的两个三角形相似.
A'
B'
C'
B
A
C
D
E
A: ( )
B: ( )
C: ( )
D: ( )
A
B
C
D
E
如图,DE∥BC,判断下列各式是否正确:
1.本节课我们学习了三角形相似的哪种判定方法?这种判定方法的前提条件是什么?
2.我们是如何证明判定方法的?
1:判断图中的两个三角形是否相似.
15
20
25
27
36
45
2:判断图中的两个三角形是否相似,并求出 x和∠A.
56°
54
45
36
30
20
x
A
B
C
D
E
3:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
F
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
1.对应角 ,对应边的 的两个三角形,叫做相似三角形.
相等
比相等
对应角相等
比相等
∠A=∠D,∠B=∠E,∠C=∠F.
如果△ABC∽△DEF,那么
2.相似三角形的 ,各对应边的 .
学习三角形全等时,我们知道,除了可以验证所有的角和边分别相等来判定两个三角形全等外,还有判定的简便方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
27.2.1 相似三角形的判定
人教版八年级数学 下册
1.掌握相似三角形的判定定理.
2.综合运用相似三角形的判定定理来解决问题.
3.进一步体验类比的学习思想.
请同学们阅读教材27.2.1 相似三角形的判定部分,理解并掌握其基本内容,初步归纳相似三角形的判定方法。
即对应角相等,对应边成比例,我们说△ABC与△DEF
相似,记作△ABC∽△DEF,△ABC 和△DEF的相似比
为 k, △DEF 与△ABC 的相似比为 .
∠A=∠D,∠B=∠E,∠C=∠F, ,
为了证明相似三角形的判定定理,我们先来学习下面的平行线分线段成比例这个基本事实.
定义:在△ABC 和△DEF中,如果
问题 如图,任意画两条直线a,b ,再画三条与a,b 都相交的平行线l1,l2,l3 .探究l1,l2,l3在直线 a,b 上截得的线段有什么关系.
通过计算可以得到:
等.
,
,
,
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
说明:
① 定理的条件是“两条直线被一组平行线所截”;
② 是“对应线段成比例”,注意“对应”两字.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
用定义证明△ADE∽△ABC, 需要具备的条件:
角:∠A=∠A,∠ADE=∠B,∠AED=∠C;
A
B
C
D
E
判定三角形相似的定理:
边: .
F
如何证明呢?
问题: 成立吗?
如图 l1∥l2∥l3,试根据图形写出成比例线段.
.
,
,
,
,
,
判定方法:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
问题2:在△ABC 与△ 中,如果满足∠B= ∠B',∠C=∠C',那么能否判定这两个三角形相似?
判定方法:两角分别相等的两个三角形相似.
A'
B'
C'
B
A
C
D
E
A: ( )
B: ( )
C: ( )
D: ( )
A
B
C
D
E
如图,DE∥BC,判断下列各式是否正确:
1.本节课我们学习了三角形相似的哪种判定方法?这种判定方法的前提条件是什么?
2.我们是如何证明判定方法的?
1:判断图中的两个三角形是否相似.
15
20
25
27
36
45
2:判断图中的两个三角形是否相似,并求出 x和∠A.
56°
54
45
36
30
20
x
A
B
C
D
E
3:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
F
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
