人教版九年级数学 下册 27.2.2相似三角形的性质 课件(共24张PPT)
文档属性
| 名称 | 人教版九年级数学 下册 27.2.2相似三角形的性质 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 767.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 15:22:06 | ||
图片预览







文档简介
(共24张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
27.2.2 相似三角形的性质
人教版八年级数学 下册
目标导航
1.掌握相似三角形的性质定理.
2.综合运用相似三角形的性质定理来解决问题.
3.进一步体验类比的学习思想.
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比相等
对应角相等 对应角相等
对应高相等 对应高的比?
对应中线相等 对应中线的比?
对应角平分线相等 对应角平分线的比?
周长相等 周长的比?
面积相等 面积的比?
类比学习
认真阅读课本27.2.2相似三角形的性质部分内容,完成下面练习并体验知识点的形成过程。
自主研学
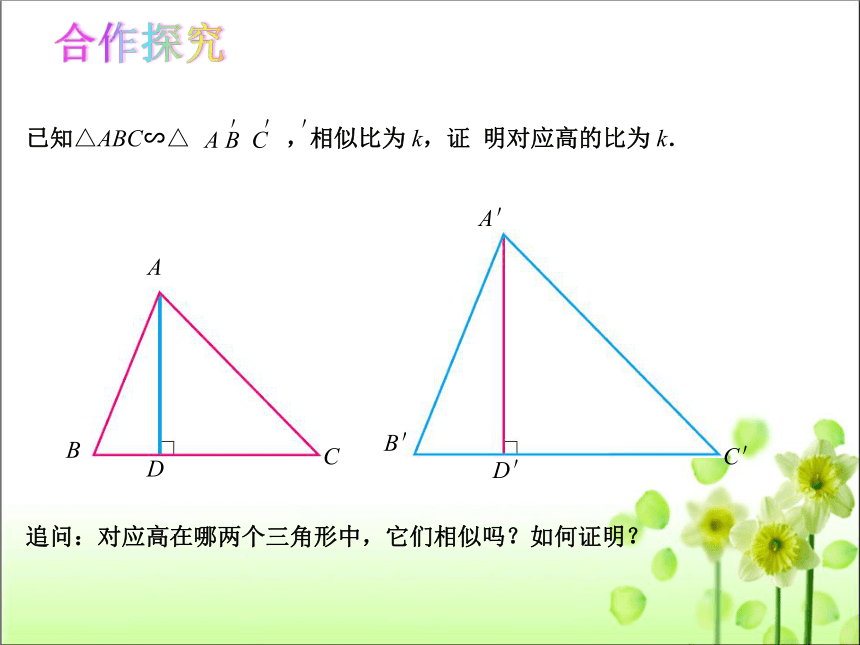
已知△ABC∽△ ,相似比为 k,证 明对应高的比为 k.
追问:对应高在哪两个三角形中,它们相似吗?如何证明?
A'
B'
D'
C'
A
B
D
C
'
'
'
A B C
合作探究
结论:
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
如果△ ABC∽△ ,相似比为 k,它们的对应中线、角平分线的比是否也等于相似比?
'
'
'
A B C
合作探究
两个相似三角形的_______相等,_______成比例。
_________________________、
____________________________、
________________________________都等于相似比。
对应角
对应边
相似三角形对应高的比
相似三角形对应中线的比
相似三角形对应角平分线的比
合作探究
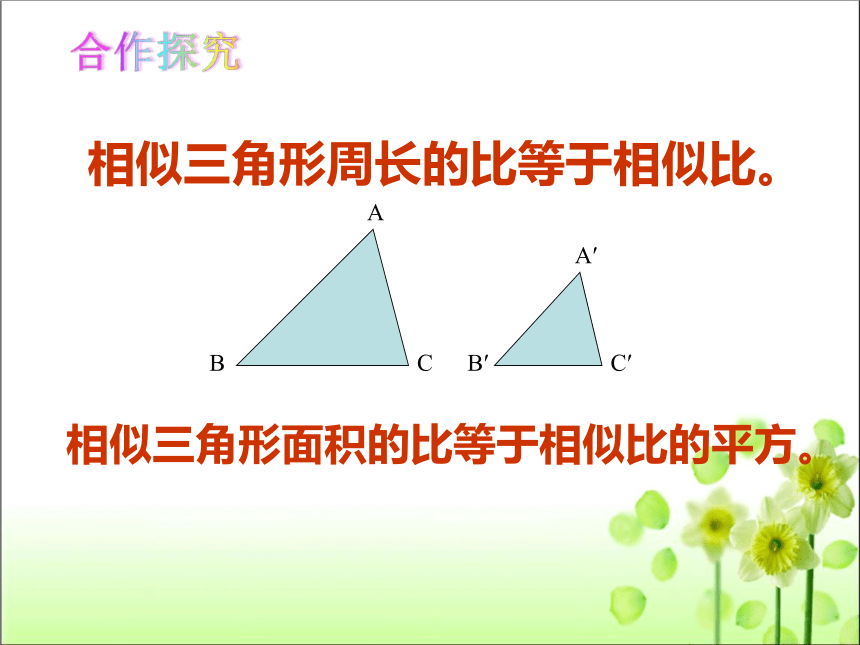
相似三角形周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
A
C
B
B′
A′
C′
合作探究
相似三角形周长的比等于相似比。
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
合作探究
相似三角形面积的比等于相似比的平方。
已知:
求证:
∽△
△
A
B
C
A′
B′
C′
D
D′
证明:
分别过A、A′,
作AD⊥BC于D,
∴
∵
∽ △
△
∴
∴
(相似三角形对应边成比例)
合作探究
例1:已知 : ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
解:∵
∽△
△
∴
(相似三角形周长的比等于相似比)
∵AB=15cm,
∴
∴
=18cm ,BC=20cm
∴
AC=60-15-20=25cm
=72-18-24=30cm
合作探究
例2:如图所示,D、E分别是AC、AB上的点,
A
B
C
D
E
已知△ABC的面积为 ,
求四边形BCDE的面积。
解:∵
,∠A=∠A
∴
∽△
△
∴
(相似三角形面积的比等于相似比的平方)
∴
∵
∴
∴
∴
(两边对应成比例,且夹角相等,两三角形相似)
合作探究
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
1.相似三角形对应边的比为3∶5 ,那么相似比为___________,对应角的角平分线的比为______,周长的比为_____,面积的比为_____。
变化:相似三角形对应边的比为9∶8?
相似三角形对应边的比为0.5?
2.两个相似三角形对应高的比为2:5,则对应角平分线的比为____, 周长比为___ .
3.两个相似三角形对应中线的比为1:4,则对应高的比为______ ,面积比为______。
即学即练
今天我们学习相似三角形哪些性质?
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
课堂小结
1.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
检测目标
2、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
3、两个相似三角形对应的中线长分别是6cm和
18cm,若较大三角形的周长是42cm,面积是
12 ,则较小三角形的周长为________cm,
面积为____ 。
1:2
1:4
检测目标
4、已知:如图△ABC中,DE∥BC,AF⊥DE
垂足为F,AF交BC于G。若AF=5,FG=3,
则
A
F
E
D
B
C
G
H
N
M
F
E
D
C
B
A
5、如图在 ABCD中,E是BC的中点,F是BE的中点,
AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。
5
8
5
8
25
64
1:4
检测目标
6、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。
A
B
C
D
E
检测目标
7、已知: ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
27.2.2 相似三角形的性质
人教版八年级数学 下册
目标导航
1.掌握相似三角形的性质定理.
2.综合运用相似三角形的性质定理来解决问题.
3.进一步体验类比的学习思想.
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比相等
对应角相等 对应角相等
对应高相等 对应高的比?
对应中线相等 对应中线的比?
对应角平分线相等 对应角平分线的比?
周长相等 周长的比?
面积相等 面积的比?
类比学习
认真阅读课本27.2.2相似三角形的性质部分内容,完成下面练习并体验知识点的形成过程。
自主研学
已知△ABC∽△ ,相似比为 k,证 明对应高的比为 k.
追问:对应高在哪两个三角形中,它们相似吗?如何证明?
A'
B'
D'
C'
A
B
D
C
'
'
'
A B C
合作探究
结论:
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
如果△ ABC∽△ ,相似比为 k,它们的对应中线、角平分线的比是否也等于相似比?
'
'
'
A B C
合作探究
两个相似三角形的_______相等,_______成比例。
_________________________、
____________________________、
________________________________都等于相似比。
对应角
对应边
相似三角形对应高的比
相似三角形对应中线的比
相似三角形对应角平分线的比
合作探究
相似三角形周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
A
C
B
B′
A′
C′
合作探究
相似三角形周长的比等于相似比。
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
合作探究
相似三角形面积的比等于相似比的平方。
已知:
求证:
∽△
△
A
B
C
A′
B′
C′
D
D′
证明:
分别过A、A′,
作AD⊥BC于D,
∴
∵
∽ △
△
∴
∴
(相似三角形对应边成比例)
合作探究
例1:已知 : ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
解:∵
∽△
△
∴
(相似三角形周长的比等于相似比)
∵AB=15cm,
∴
∴
=18cm ,BC=20cm
∴
AC=60-15-20=25cm
=72-18-24=30cm
合作探究
例2:如图所示,D、E分别是AC、AB上的点,
A
B
C
D
E
已知△ABC的面积为 ,
求四边形BCDE的面积。
解:∵
,∠A=∠A
∴
∽△
△
∴
(相似三角形面积的比等于相似比的平方)
∴
∵
∴
∴
∴
(两边对应成比例,且夹角相等,两三角形相似)
合作探究
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
1.相似三角形对应边的比为3∶5 ,那么相似比为___________,对应角的角平分线的比为______,周长的比为_____,面积的比为_____。
变化:相似三角形对应边的比为9∶8?
相似三角形对应边的比为0.5?
2.两个相似三角形对应高的比为2:5,则对应角平分线的比为____, 周长比为___ .
3.两个相似三角形对应中线的比为1:4,则对应高的比为______ ,面积比为______。
即学即练
今天我们学习相似三角形哪些性质?
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
课堂小结
1.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
检测目标
2、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
3、两个相似三角形对应的中线长分别是6cm和
18cm,若较大三角形的周长是42cm,面积是
12 ,则较小三角形的周长为________cm,
面积为____ 。
1:2
1:4
检测目标
4、已知:如图△ABC中,DE∥BC,AF⊥DE
垂足为F,AF交BC于G。若AF=5,FG=3,
则
A
F
E
D
B
C
G
H
N
M
F
E
D
C
B
A
5、如图在 ABCD中,E是BC的中点,F是BE的中点,
AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。
5
8
5
8
25
64
1:4
检测目标
6、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。
A
B
C
D
E
检测目标
7、已知: ,它们的周长分别 为60cm和72cm,且AB=15cm,
∽△
△
=24cm。
求:BC、AC、 、
A
B
C
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
