湘教版八年级数学下册课件2.7正方形(25张)
文档属性
| 名称 | 湘教版八年级数学下册课件2.7正方形(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览








文档简介
课件25张PPT。第二章
四边形八年级数学湘教版·下册2.7 正方形学习目标
1.掌握正方形的性质及判定方法.(重点)
2.会运用正方形的性质及判定条件进行有关的论证和
计算.(难点)新课引入
活动:观察这些图片,你什么发现?正方形四条边有什么关系?四个角呢?新知探究
活动1:准备一张矩形的纸片,按照下图折叠,然后展开,得到一个四边形.问题1:折叠后得到的特殊四边形是什么四边形?正方形活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.问题2:经过变化后得到特殊四边形是什么四边形?有一组邻边相等,并且有一个角是直角的平行四边形是正方形. 正方形新知探究
新知探究
ABCD角:
边:
对角线:
对称性:
四个角都是直角.四条边相等.对角线相等且互相垂直平分.aaaa轴对称图形(4条对称轴). 1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.填一填:中心对称图形.新知探究已知:如右图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.ABCD证明:∵四边形ABCD是正方形 ,
∴∠A=90°, AB=BC . (正方形的定义)
又∵正方形是平行四边形.
∴正方形是矩形, (矩形的定义)
正方形是菱形.(菱形的定义)
∴∠A=∠B =∠C =∠D = 90°,
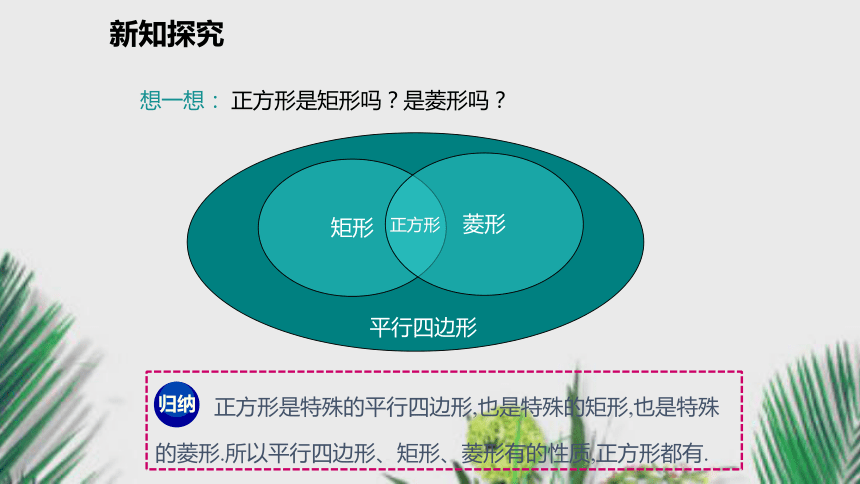
AB= BC=CD=AD.定理证明新知探究已知:如右图 , 四边形ABCD是正方形 . 对角线AC , BD相交于点O.求证:AO=BO=CO=DO , AC⊥BD. ABCDO请同学们动手完成以上证明?提示:可以先通过证明来得到正方形是矩形、菱形,然后利用矩形和菱形的定理来完成该题.新知探究想一想: 正方形是矩形吗?是菱形吗? 矩形菱形正方形平行四边形 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以平行四边形、矩形、菱形有的性质,正方形都有.新知探究归纳结论正方形对角线边边对角线对角线角对边平行且相等相互平分相等四个角相等都是90°相互垂直且
平分对角四边相等对称性轴对称图形(4条对称轴)新知探究例1:如图在正方形ABCD中, E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.典例精析解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形,
∴BC=DC,∠BCE =90° .
(正方形的四条边都相等,四个角都是直角).
∴∠DCF=180°-∠BCE=180°-90°=90°,ABDCFE新知探究ABDFE∴∠BCE=∠DCF.
又∵CE=CF,
∴△BCE ≌△DCF,
∴BE=DF.
(2)延长BE交DF于点M,
∵△BCE ≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°,∴∠CBE+∠F=90° , ∴∠BMF=90°.
∴BE⊥DF.CM新知探究动一动:过点A作射线AM的垂线AN,分别在AM , AN上取点B , D ,使AB=AD ,作DC∥AB , BC∥AD ,得四边形ABCD.AMNBDC问题1:上面所画四边形ABCD是正方形吗?为什么?新知探究想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?(1)(2)(3)(4)新知探究菱形问题2:满足怎样条件的矩形是正方形?矩形正方形一组邻边相等对角线互相垂直问题3:满足怎样条件的菱形是正方形?正方形一个角是直角对角线相等新知探究 1.对角线相等的菱形是正方形.
2.对角线垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.正方形判定的两条途径:正方形正方形++先判定菱形先判定矩形矩形条件菱形条件(1)(2)一个直角对角线相等一组邻边相等对角线垂直新知探究例2:如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.典例精析FABECD解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形;45°45°新知探究FABECD证明: ∵ BF∥CE , CF∥BE ,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°.
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.新知探究做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?矩形正方形任意四边形平行四边形菱形正方形EFGHEFGHEFGH课堂小结1.四个角都是直角2.四条边都相等3.对角线相等且互相垂直平分正方形性质定义有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形课堂小结有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 平行四边形矩形菱形正方形一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 课堂小测1.下列命题正确的是( )
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
2.四个内角都相等的四边形一定是( )
A.正方形 B.菱形 C.矩形 D.平行四边形DC课堂小测3.在正方形ABC中,∠ADB= ,∠DAC= , ∠BOC= .
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .45°90°22.5°第3题第4题45°课堂小测3.如图 , 已知正方形ABCD , 以AB为边向正方形外作等边△ABE,连接DE , CE ,求∠DEC的度数. DAEBC解:∵△ABE是等边三角形 ,
∴ AB =AE=BE,
∠ABE=∠BEA=∠EAB =60°.
又∵四边形ABCD是正方形.
∴AD=BC=AE=BE,
∠DAB=∠ABC=90° ,
∴∠DAE=∠CBE=150° ,
∴∠AED=∠EDA=∠CEB=∠BCE=15° ,
∴∠DEC=∠AEB-∠AED-∠CEB=30°.课堂小测4.已知:如图所示,在Rt△ABC中, ∠C=90° , ∠BAC , ∠ABC的平分线于点D , DE⊥BC于点E , DF⊥AC于点F.
求证:四边形CEDF是正方形.证明: 如图所示,过点D作DG⊥AB于点G.
∵DF⊥AC , DE⊥BC ,
∴∠DFC=∠DEC=90°.
又∠C=90°,
∴四边形CEDF是矩形 (有三个角是直角的四边形是矩形).
∴AD平分∠BAC , DF⊥AC , DG⊥AB ,
∴DF=DG. 同理可得DE=DG , ∴DE=DF.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).CEBAFDG
1.掌握正方形的性质及判定方法.(重点)
2.会运用正方形的性质及判定条件进行有关的论证和
计算.(难点)新课引入
活动:观察这些图片,你什么发现?正方形四条边有什么关系?四个角呢?新知探究
活动1:准备一张矩形的纸片,按照下图折叠,然后展开,得到一个四边形.问题1:折叠后得到的特殊四边形是什么四边形?正方形活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.问题2:经过变化后得到特殊四边形是什么四边形?有一组邻边相等,并且有一个角是直角的平行四边形是正方形. 正方形新知探究
新知探究
ABCD角:
边:
对角线:
对称性:
四个角都是直角.四条边相等.对角线相等且互相垂直平分.aaaa轴对称图形(4条对称轴). 1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.填一填:中心对称图形.新知探究已知:如右图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.ABCD证明:∵四边形ABCD是正方形 ,
∴∠A=90°, AB=BC . (正方形的定义)
又∵正方形是平行四边形.
∴正方形是矩形, (矩形的定义)
正方形是菱形.(菱形的定义)
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.定理证明新知探究已知:如右图 , 四边形ABCD是正方形 . 对角线AC , BD相交于点O.求证:AO=BO=CO=DO , AC⊥BD. ABCDO请同学们动手完成以上证明?提示:可以先通过证明来得到正方形是矩形、菱形,然后利用矩形和菱形的定理来完成该题.新知探究想一想: 正方形是矩形吗?是菱形吗? 矩形菱形正方形平行四边形 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以平行四边形、矩形、菱形有的性质,正方形都有.新知探究归纳结论正方形对角线边边对角线对角线角对边平行且相等相互平分相等四个角相等都是90°相互垂直且
平分对角四边相等对称性轴对称图形(4条对称轴)新知探究例1:如图在正方形ABCD中, E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.典例精析解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形,
∴BC=DC,∠BCE =90° .
(正方形的四条边都相等,四个角都是直角).
∴∠DCF=180°-∠BCE=180°-90°=90°,ABDCFE新知探究ABDFE∴∠BCE=∠DCF.
又∵CE=CF,
∴△BCE ≌△DCF,
∴BE=DF.
(2)延长BE交DF于点M,
∵△BCE ≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°,∴∠CBE+∠F=90° , ∴∠BMF=90°.
∴BE⊥DF.CM新知探究动一动:过点A作射线AM的垂线AN,分别在AM , AN上取点B , D ,使AB=AD ,作DC∥AB , BC∥AD ,得四边形ABCD.AMNBDC问题1:上面所画四边形ABCD是正方形吗?为什么?新知探究想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?(1)(2)(3)(4)新知探究菱形问题2:满足怎样条件的矩形是正方形?矩形正方形一组邻边相等对角线互相垂直问题3:满足怎样条件的菱形是正方形?正方形一个角是直角对角线相等新知探究 1.对角线相等的菱形是正方形.
2.对角线垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.正方形判定的两条途径:正方形正方形++先判定菱形先判定矩形矩形条件菱形条件(1)(2)一个直角对角线相等一组邻边相等对角线垂直新知探究例2:如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.典例精析FABECD解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形;45°45°新知探究FABECD证明: ∵ BF∥CE , CF∥BE ,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°.
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.新知探究做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?矩形正方形任意四边形平行四边形菱形正方形EFGHEFGHEFGH课堂小结1.四个角都是直角2.四条边都相等3.对角线相等且互相垂直平分正方形性质定义有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形课堂小结有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 平行四边形矩形菱形正方形一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 课堂小测1.下列命题正确的是( )
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
2.四个内角都相等的四边形一定是( )
A.正方形 B.菱形 C.矩形 D.平行四边形DC课堂小测3.在正方形ABC中,∠ADB= ,∠DAC= , ∠BOC= .
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .45°90°22.5°第3题第4题45°课堂小测3.如图 , 已知正方形ABCD , 以AB为边向正方形外作等边△ABE,连接DE , CE ,求∠DEC的度数. DAEBC解:∵△ABE是等边三角形 ,
∴ AB =AE=BE,
∠ABE=∠BEA=∠EAB =60°.
又∵四边形ABCD是正方形.
∴AD=BC=AE=BE,
∠DAB=∠ABC=90° ,
∴∠DAE=∠CBE=150° ,
∴∠AED=∠EDA=∠CEB=∠BCE=15° ,
∴∠DEC=∠AEB-∠AED-∠CEB=30°.课堂小测4.已知:如图所示,在Rt△ABC中, ∠C=90° , ∠BAC , ∠ABC的平分线于点D , DE⊥BC于点E , DF⊥AC于点F.
求证:四边形CEDF是正方形.证明: 如图所示,过点D作DG⊥AB于点G.
∵DF⊥AC , DE⊥BC ,
∴∠DFC=∠DEC=90°.
又∠C=90°,
∴四边形CEDF是矩形 (有三个角是直角的四边形是矩形).
∴AD平分∠BAC , DF⊥AC , DG⊥AB ,
∴DF=DG. 同理可得DE=DG , ∴DE=DF.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).CEBAFDG
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
