湘教版八年级数学下册课件2.1.2 多边形的外角和(15张)
文档属性
| 名称 | 湘教版八年级数学下册课件2.1.2 多边形的外角和(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览



文档简介
课件15张PPT。第二章
四边形八年级数学湘教版·下册2.1.2 多边形的外角和学习目标
1.了解多边形的外角定义,并能准确找出多边形的外角.
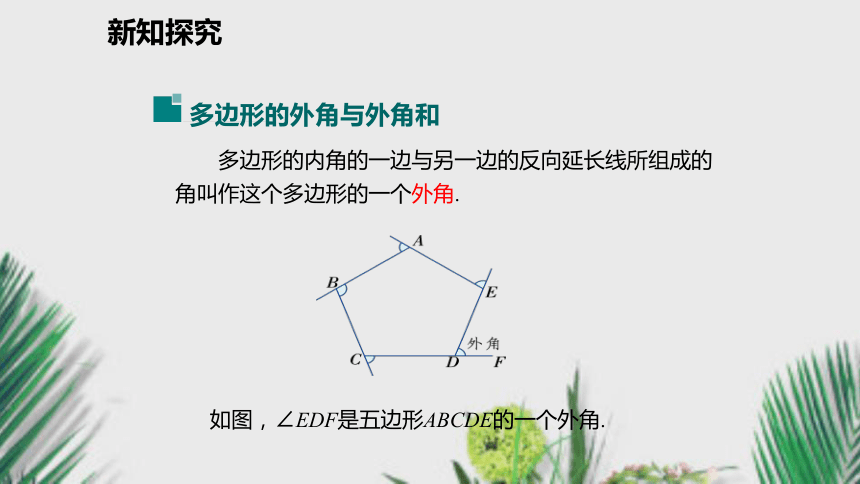
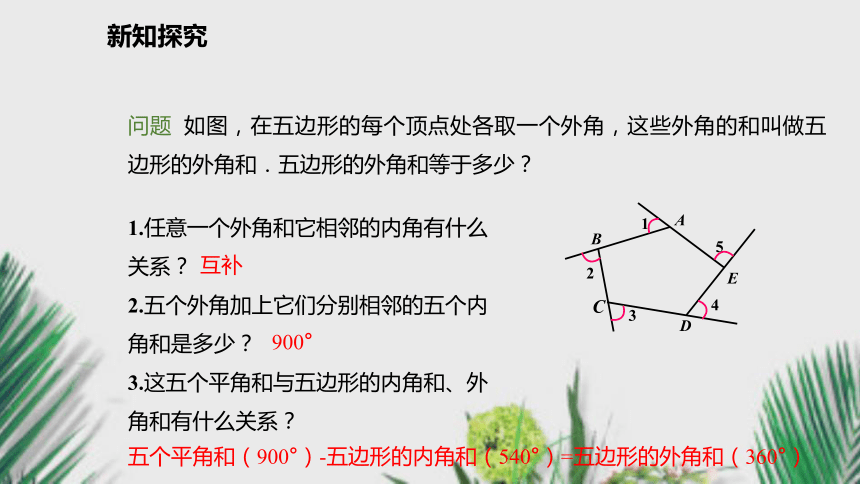
2.运用多边形的外角和解决问题.(重点)新课导入提问引入1.多边形的内角和是什么?2.你还记得三角形的外角是怎样定义的吗?三角形的外角和是多少呢?n边形的内角和等于(n-2) · 180° 三角形的内角的一边与另一边的反向延长线所组成的角叫作三角形的外角.其外角和为360°.新知探究 多边形的内角的一边与另一边的反向延长线所组成的角叫作这个多边形的一个外角. 如图,∠EDF是五边形ABCDE的一个外角.新知探究问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
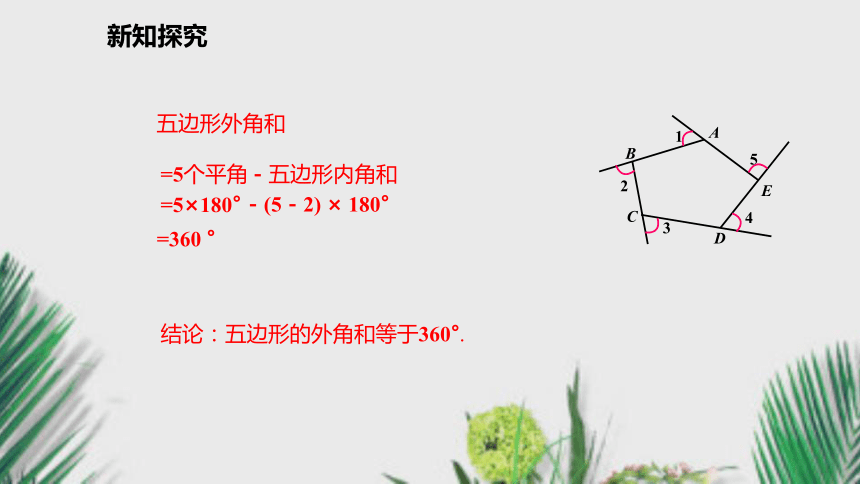
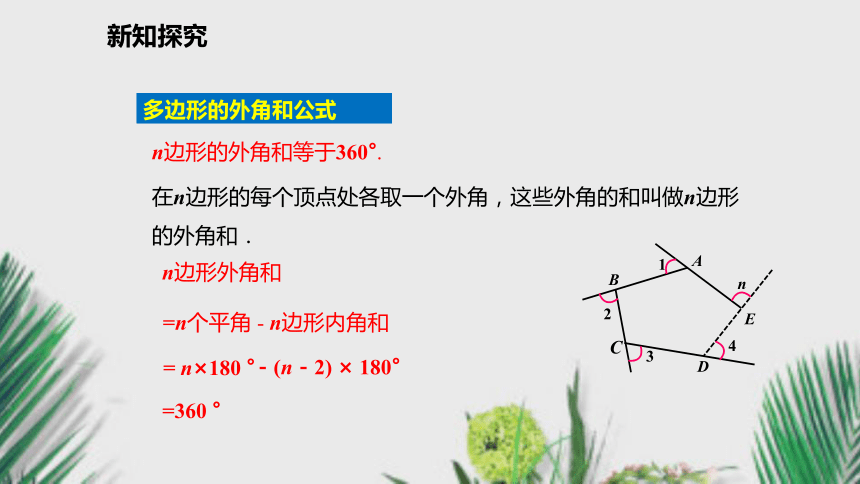
3.这五个平角和与五边形的内角和、外角和有什么关系?互补900°五个平角和(900°)-五边形的内角和(540°)=五边形的外角和(360°)新知探究五边形外角和=360 °=5个平角-五边形内角和=5×180°-(5-2) × 180°结论:五边形的外角和等于360°.新知探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和n边形的外角和等于360°.-(n-2) × 180°=360 °=n个平角 - n边形内角和= n×180 °多边形的外角和公式新知探究回想正多边形的性质 , 你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?每个内角的度数是每个外角的度数是练一练:(1)若一个正多边形的内角是120°, 那么这是正____边形.
(2)已知多边形的每个外角都是45°, 则这个多边形是______边形.六正八新知探究例1: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.解: 设多边形的边数为n.
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360°,
∴ (n-2)?180°=2× 360o.
解得 n=6.
∴这个多边形的边数为6.12新知探究例2: 已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.解:设这个多边形的内角为7x °,外角为2x°.
根据题意得7x+2x=180,解得x=20.即每个内角是140 °,每个外角是40 °.360° ÷40 °=9.答:这个多边形是九边形.还有其他解法吗?新知探究解:设这个多边形的边数为n,根据题意得解得n=9.答:这个多边形是九边形.课堂小结多边形的外角与外角和外角和多边形的外角和等于360°
特别注意:与边数无关正多
边形内角= ,外角=
课堂小测1.判断.
(1)当多边形边数增加时,它的内角和也随着增加. ( )
(2)当多边形边数增加时,它的外角和也随着增加. ( )
(3)三角形的外角和与八边形的外角和相等. ( )
(4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形.( )2.五边形的内角和为 ,它的对角线有 条.540°53.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.180°0°课堂小测4.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °D5.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540 ° C.720 ° D.900 °C课堂小测能力提升: 一个多边形所有内角与一个外角的和是2380°,则这个多边形的边数为___.15解析:设这个多边形的边数为x(x为正整数),则这个多边形的内角和为(x-2)×180°,由题意可得:
2380-180<(x-2)×180°<2380,
解得14.22因为x为正整数,所以x=15,即这个多边形的边数为15.
1.了解多边形的外角定义,并能准确找出多边形的外角.
2.运用多边形的外角和解决问题.(重点)新课导入提问引入1.多边形的内角和是什么?2.你还记得三角形的外角是怎样定义的吗?三角形的外角和是多少呢?n边形的内角和等于(n-2) · 180° 三角形的内角的一边与另一边的反向延长线所组成的角叫作三角形的外角.其外角和为360°.新知探究 多边形的内角的一边与另一边的反向延长线所组成的角叫作这个多边形的一个外角. 如图,∠EDF是五边形ABCDE的一个外角.新知探究问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?互补900°五个平角和(900°)-五边形的内角和(540°)=五边形的外角和(360°)新知探究五边形外角和=360 °=5个平角-五边形内角和=5×180°-(5-2) × 180°结论:五边形的外角和等于360°.新知探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和n边形的外角和等于360°.-(n-2) × 180°=360 °=n个平角 - n边形内角和= n×180 °多边形的外角和公式新知探究回想正多边形的性质 , 你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?每个内角的度数是每个外角的度数是练一练:(1)若一个正多边形的内角是120°, 那么这是正____边形.
(2)已知多边形的每个外角都是45°, 则这个多边形是______边形.六正八新知探究例1: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.解: 设多边形的边数为n.
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360°,
∴ (n-2)?180°=2× 360o.
解得 n=6.
∴这个多边形的边数为6.12新知探究例2: 已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.解:设这个多边形的内角为7x °,外角为2x°.
根据题意得7x+2x=180,解得x=20.即每个内角是140 °,每个外角是40 °.360° ÷40 °=9.答:这个多边形是九边形.还有其他解法吗?新知探究解:设这个多边形的边数为n,根据题意得解得n=9.答:这个多边形是九边形.课堂小结多边形的外角与外角和外角和多边形的外角和等于360°
特别注意:与边数无关正多
边形内角= ,外角=
课堂小测1.判断.
(1)当多边形边数增加时,它的内角和也随着增加. ( )
(2)当多边形边数增加时,它的外角和也随着增加. ( )
(3)三角形的外角和与八边形的外角和相等. ( )
(4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形.( )2.五边形的内角和为 ,它的对角线有 条.540°53.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.180°0°课堂小测4.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °D5.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540 ° C.720 ° D.900 °C课堂小测能力提升: 一个多边形所有内角与一个外角的和是2380°,则这个多边形的边数为___.15解析:设这个多边形的边数为x(x为正整数),则这个多边形的内角和为(x-2)×180°,由题意可得:
2380-180<(x-2)×180°<2380,
解得14.22
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
