湘教版八年级数学下册课件2.2.2.2平行四边形的判定定理3(14张)
文档属性
| 名称 | 湘教版八年级数学下册课件2.2.2.2平行四边形的判定定理3(14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览




文档简介
课件14张PPT。第二章
四边形八年级数学湘教版·下册2.2.2.2 平行四边形的判定定理3学习目标
1.利用对角线互相平分判定平行四边形;(重点)
2.利用两组对角分别相等判定平行四边形.新课导入平行四边形的判定方法:判定定理1 一组对边平行且相等的四边形是平行四边形.判定定理2 两组对边分别相等的四边形是平行四边形.新知探究工具:两支长度不相等的铅笔.动手:能利用这两支笔摆出一个平行
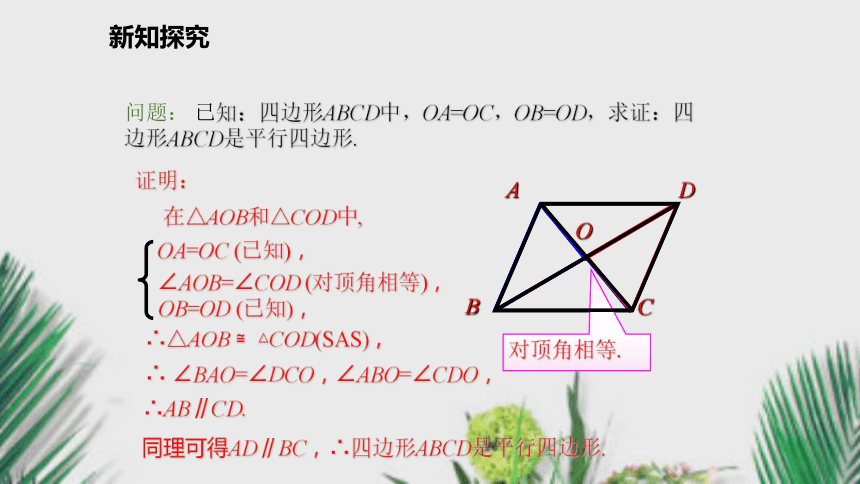
四边形吗?试试看!合作探究新知探究问题: 已知:四边形ABCD中,OA=OC,OB=OD,求证:四边形ABCD是平行四边形.证明:对顶角相等.在△AOB和△COD中,OA=OC (已知),OB=OD (已知),∠AOB=∠COD (对顶角相等),∴△AOB ≌△COD(SAS),∴ ∠BAO=∠DCO,∠ABO=∠CDO,∴AB∥CD.
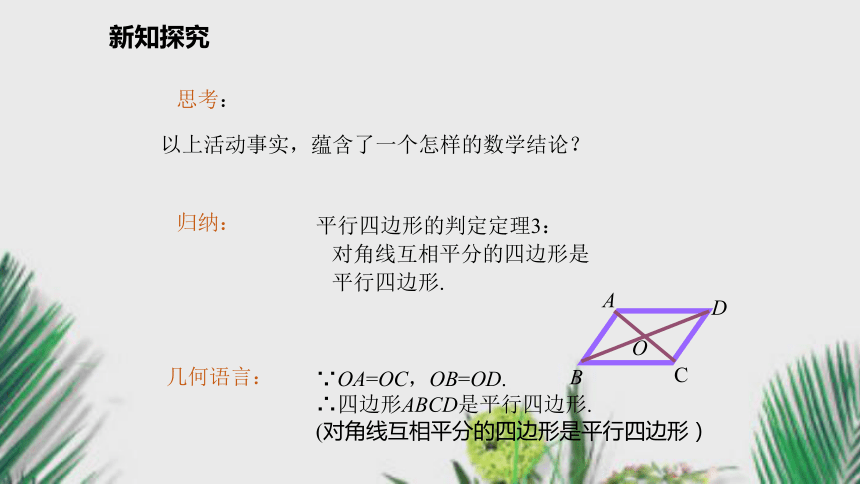
同理可得AD∥BC,∴四边形ABCD是平行四边形.新知探究 以上活动事实,蕴含了一个怎样的数学结论?平行四边形的判定定理3:
对角线互相平分的四边形是
平行四边形.∵OA=OC,OB=OD.
∴四边形ABCD是平行四边形.
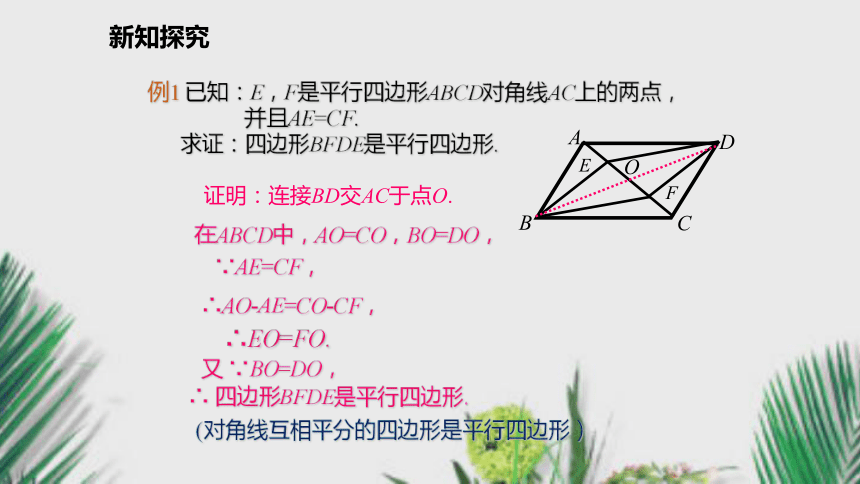
(对角线互相平分的四边形是平行四边形)思考:归纳:几何语言:新知探究例1 已知:E,F是平行四边形ABCD对角线AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.O证明:连接BD交AC于点O.在ABCD中,AO=CO,BO=DO,∵AE=CF,
∴AO-AE=CO-CF,∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)新知探究例2 已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
试问:四边 形ABCD是平行四边形吗?请说明理由.解:是平行四边形.理由如下:∵∠A+∠C+∠B+∠D=360°,又∵∠A=∠C ,∠B=∠D ,∴ AD∥BC.∴四边形ABCD是平行四边形。∴2∠A+2∠B=360°,即∠A+∠B=180°,同理得 AB∥CD,新知探究由上述证明可以得到平行四边形的判定定理:两组对角分别相等的四边形是平行四边形.几何语言描述判定:∠A=∠C
∠B=∠D课堂小结 判定 1 定义:两组对边分别平行的四边形是平行四边形 判定2 两组对边分别相等的四边形是平行四边形 判定3 两组对角分别相等的四边形是平行四边形 判定4 两条对角线互相平分的四边形是平行四边形 判定5 一组对边平行且相等的四边形是平行四边形平行四边形的判定定理:1.下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )课堂小测A.1:2:3:4 C.2:3:2:3 B.2:2:3:3 需要两组对角分别相等.D.2:3:3:2C课堂小测2.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°D课堂小测 若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?C课堂小测4.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
∴△ABE ≌△FCE(AAS),∴AE=EF.
又∵BE=CE,∴四边形ABFC是平行四边形.解:四边形ABFC是平行四边形 . 理由如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E是BC的中点,
∴BE=CE. 在△ABE和△FCE中,
1.利用对角线互相平分判定平行四边形;(重点)
2.利用两组对角分别相等判定平行四边形.新课导入平行四边形的判定方法:判定定理1 一组对边平行且相等的四边形是平行四边形.判定定理2 两组对边分别相等的四边形是平行四边形.新知探究工具:两支长度不相等的铅笔.动手:能利用这两支笔摆出一个平行
四边形吗?试试看!合作探究新知探究问题: 已知:四边形ABCD中,OA=OC,OB=OD,求证:四边形ABCD是平行四边形.证明:对顶角相等.在△AOB和△COD中,OA=OC (已知),OB=OD (已知),∠AOB=∠COD (对顶角相等),∴△AOB ≌△COD(SAS),∴ ∠BAO=∠DCO,∠ABO=∠CDO,∴AB∥CD.
同理可得AD∥BC,∴四边形ABCD是平行四边形.新知探究 以上活动事实,蕴含了一个怎样的数学结论?平行四边形的判定定理3:
对角线互相平分的四边形是
平行四边形.∵OA=OC,OB=OD.
∴四边形ABCD是平行四边形.
(对角线互相平分的四边形是平行四边形)思考:归纳:几何语言:新知探究例1 已知:E,F是平行四边形ABCD对角线AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.O证明:连接BD交AC于点O.在ABCD中,AO=CO,BO=DO,∵AE=CF,
∴AO-AE=CO-CF,∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)新知探究例2 已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
试问:四边 形ABCD是平行四边形吗?请说明理由.解:是平行四边形.理由如下:∵∠A+∠C+∠B+∠D=360°,又∵∠A=∠C ,∠B=∠D ,∴ AD∥BC.∴四边形ABCD是平行四边形。∴2∠A+2∠B=360°,即∠A+∠B=180°,同理得 AB∥CD,新知探究由上述证明可以得到平行四边形的判定定理:两组对角分别相等的四边形是平行四边形.几何语言描述判定:∠A=∠C
∠B=∠D课堂小结 判定 1 定义:两组对边分别平行的四边形是平行四边形 判定2 两组对边分别相等的四边形是平行四边形 判定3 两组对角分别相等的四边形是平行四边形 判定4 两条对角线互相平分的四边形是平行四边形 判定5 一组对边平行且相等的四边形是平行四边形平行四边形的判定定理:1.下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )课堂小测A.1:2:3:4 C.2:3:2:3 B.2:2:3:3 需要两组对角分别相等.D.2:3:3:2C课堂小测2.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°D课堂小测 若一组对边平行,另一组对边相等,这个四边形是平行四边形吗?C课堂小测4.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
∴△ABE ≌△FCE(AAS),∴AE=EF.
又∵BE=CE,∴四边形ABFC是平行四边形.解:四边形ABFC是平行四边形 . 理由如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E是BC的中点,
∴BE=CE. 在△ABE和△FCE中,
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
