人教B版 必修5 高二数学 2.2.2等差数列的前n项和 教学课件(共40张PPT)
文档属性
| 名称 | 人教B版 必修5 高二数学 2.2.2等差数列的前n项和 教学课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 704.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 13:33:29 | ||
图片预览









文档简介
(共40张PPT)
回顾旧知
等差数列{an}的通项公式:an=a1+(n-1)d
也可整理为an=dn+(a1-d)
值得注意的是:
n=1时必须得成立,才能这样写通项公式。
新课导入
一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支.这个V形架上共放着多少支铅笔?
问题就是求“1+2+3+4+…+100=?”
高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,…,每组数的和均相等,都等于101,50个101就等于5050了.高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
学了之后你会发现你比高斯聪明
2.2.2 等差数列的前n项和
教学目标
知识与能力
(1)掌握等差数列前n项和公式.
(2)掌握等差数列前n项和公式的推导过程.
(3)会简单运用等差数列的前n项和公式.
过程与方法
(1)通过对等差数列前n项和公式的推导过程,渗透倒序相加求和的数学方法.
(2)通过公式的运用体会方程的思想.
(3)通过运用公式的过程,提高学生类比化归、数形结合的能力.
情感态度与价值观
结合具体模型,将教材知识和实际生活联系起来,使学生感受数学的实用性,有效激发学习兴趣,并通过对等差数列求和历史的了解,渗透数学史和数学文化.
教学重难点
重点:
等差数列前n项和的公式,有关等差数列问题求解的基本方法.
难点:
获得递推公式的思路,等差数列前n项和公式的其他形式.
思考:图案中,第1层到第21层一共有多少颗宝石?用什么办法做呢?
这是求奇数个项的和的问题,能不能直接用高斯的办法呢求和呢?
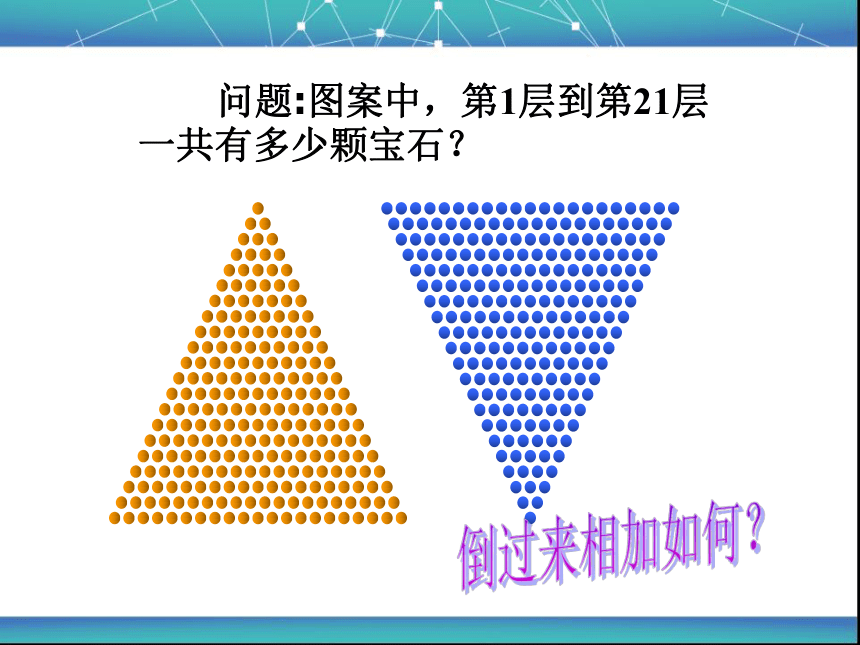
问题:图案中,第1层到第21层一共有多少颗宝石?
倒过来相加如何?
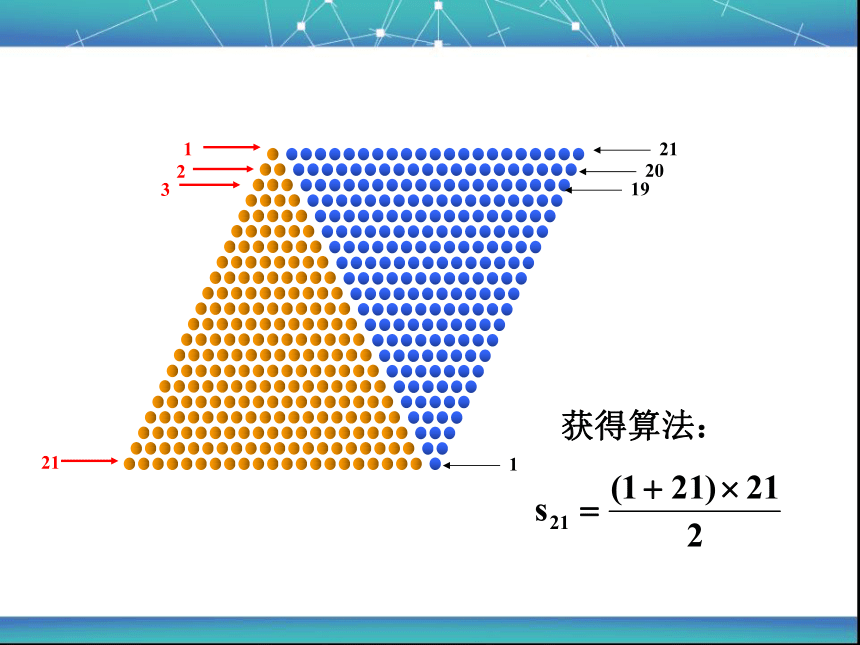
21
21
20
19
1
1
2
3
获得算法:
设等差数列 {an} 的首项为a1,公差为d,如何求等差数列的前n项和Sn= a1 +a2+a3+…+an?
设等差数列a1,a2,a3,…
它的前n 项和是 Sn=a1+a2+…+an-1+an (1)
若把次序颠倒是 Sn=an+an-1+…+a2+a1 (2)
由等差数列的性质 a1+an=a2+an-1=a3+an-2=…
例 1:
解:
(1)(2)两式左右分别相加,得
这种方法叫倒序相加法.
2Sn=(a1+an)+ (a2+an-1)+ (a3+an-2)+…+
(an-2+a3)+ (an-1+a2)+ (an+a1)=n(a1+an)
能否用a1,n,d表示Sn呢?
将an=a1+(n-1)d代入
【说明】
①推导等差数列的前n项和公式的方法叫 ;
②{an}为等差数列? ,这是一个关于 的,没有 的“ ” .
倒序相加法
Sn=an2+bn
n
常数项
二次函数
( 注意 a 还可以是 0)
等差数列前n项和公式
【公式记忆】
用梯形面积公式记忆等差数列前n项和公式,这里对图形进行了割、补两种处理,对应着等差数列前n项和的两个公式.
等差数列的前n项和公式类同于 ;
梯形的面积公式
(补成平行四边形)
a1
a1
an
an
__
__
n
__
__
n
a1
a1
(n-1)d
(分割成一个平行四边形及一个三角形)
1、若数列{an}为等差数列,则s3m=3(s2m-sm)
2、若数列{an}为等差数列,且sp=q,sq=p,sp+q=-(p+q)
3、若数列项数为2n+1,则s奇+s偶=s2n+1= (a1+a2n+1)×(2n+1),s奇-s偶=an+1,
等差数列前n项和的结论
将等差数列的前n项和公式写成上
述形式,有利于求其前n项和的极值:
等差数列前n项和再认识:
a1<0,d>0 a1>0, d<0
极大值 无 有
极小值 有 无
n
sn
n
sn
a1<0, d>0,极小值
a1>0,d<0,极大值
观察上面的式子,我们可以看出它是关于n 的二次函数,从而等差数列的前n项和可以写成形如:
y = Ax2+ Bx
y = Ax+ B
通过上面的例题,对于等差数列的相关量a1、d、n、an、sn,一般确定几个量就可以确定其他量?
a1、an、n
an、sn
a1、d、an
a1、d、n
a1、an、sn
an、d、n
an、sn、n
n、sn
d、sn
d、n
a1、sn
a1、d
由以上例题可以得出:在求等差数列的前n项的和时,当知道首项和公差,或者是知道首项和末项,均可以得出.
已知等差数列an中a2+a5+a12+a15=36.
求前16项的和?
由等差数列的性质可得:
a1+a16=a2+a15=a5+a12=36/2=18
sn=(16/2 )×18=144
答:前16项的和为144.
分析:可以由等差数列性质,直接代入前n项和公式.
例 2:
解:
等差数列 -10,-6,-2,2,…前多少项的和是54?
解:
n1=9,n2=-3 (舍去)
等差数列-10,-6,-2,2,…前9项的和是54.
例3:
设题中的等差数列为{an},前n项和是 Sn,
则a1= -10,d= -6-(-10) = 4,设 Sn=54,
根据等差数列前 n项和公式,得
n要为正整数
已知一个等差数列的前10项的和是310,前20项的和是1220,求Sn.
解:
S10=310,S20=1 220
例 4:
法二:相减得5d=-110
即 d=-22
一个等差数列,共有 10 项,其中奇数项的和为 125,偶数项的和为 15,求 a 1、d.
例 5:
解:
归纳:
等差数列中,
n 为奇数,必有
n 为偶数,必有
等差数列中,a5=14,a2+ a9=31,求S12
法二:
∵ a 5 + a 6 = a 2 + a 9
∴ a 6 = 17
公差 d = a 6 -a 5 = 3
∴ a 7 = 20
= ( a 6 + a 7 )×6
= 222
例6:
解:
等差数列 { a n } 中,S 15 = 90,求 a 8
法一:a 1 + a 1 + 14d = 12
即 a 1 + a 15 = 12
即 a 1 + 7d = 6
∴ a 8 = a 1 + 7d = 6
= 6
例7:
解:
选用中项求等差数列的前 n 项之和 S n
当 n 为奇数时,S n = ____________;
当 n 为偶数时, S n = _______________________.
归纳:
南北朝时,张丘建始创等差数列求和解法。他在《张丘建算经》里给出了几个等差数列问题.
例如:“今有女子不善织布,逐日所织之布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?”
原书的解法是:“并初、末日织布数,半之,余以乘织讫日数,即得.”
思考与余味:
再如:“今有女子善织布,逐日所织的布以同数递增,初日织五尺,计织三十日,共织九匹三丈,问日增几何?”
这是一道等差数列知道前30项和,a1的值,求等差数列的公差.
课堂小结
本节课主要讲述了等差数列的前n项和公式:
① s n=n(a1+an)/2
② s n=na1+n(n-1)d/2
以及他们的推导过程,在具体使用时,不一定完全套用公式,要灵活变通.
③
1.推导等差数列前 n项和公式的方法.
2.公式的应用中的数学思想.
-------倒序相加法
-------方程思想
3.公式中五个量a1, d, an, n, sn, 已知
其中三个量,可以求其余两个.
-------知三求二
裂项求和
有些数列求和的问题,可以对相应的数列的通项公式加以变形,将其写成两项的差,这样整个数列求和的各加数都按同样的方法裂成两项之差,其中每项的被减数一定是后面某项的减数,从而经过逐项相消仅剩下有限项,可得出前n项和公式。
?????????????????????????????????????????????????????????????????.
知识要点补充
如求和: ????????????????????????????????????????????????????????????
提示:
则:
随堂练习
1、如图,一个堆放铅笔的 V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多一支,最上面一层放120支.这个V形架上共放着多少支铅笔?
由题意可知,这个V形架上共放着120层铅笔,且自下而上各层的铅笔数成等差数列,记为{an},其中 a1=1 , a120=120.根据等差数列前n项和的公式,得
答:V形架上共放着 7260支铅笔.
解:
2、在等差数列{an}中,
(2)a1=14.5,d=0.7,an=32,求Sn
(1)a3= -2,a8=12,求S10
(2)由等差数列的通项公式,得
14.5+(n-1)?0.7=32 ? n=26
(1)a1+a10 = a3+a8 = 10
解:
3、凸 n 边形各内角成等差数列,公差为 10?,最小内角为 100?,则n等于( )
(A)7 (B)8 (C)9 (D)8或 9
由题意,得 :
解得 n=8 或 n=9
B
(舍)
解:
这位长跑运动员每天的训练量成等差数列,记为{an}, 其中 a1=7500,a7=10500.
根据等差数列前n项和公式,得
答:这位长跑运动员7天共跑了63000m.
4、某长跑运动员7天里每天的训练量是:
7500, 8000 , 8500 , 9000 , 9500 , 10000 ,10500
这位运动员7天共跑了多少米? (单位:m)
解:
回顾旧知
等差数列{an}的通项公式:an=a1+(n-1)d
也可整理为an=dn+(a1-d)
值得注意的是:
n=1时必须得成立,才能这样写通项公式。
新课导入
一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支.这个V形架上共放着多少支铅笔?
问题就是求“1+2+3+4+…+100=?”
高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,…,每组数的和均相等,都等于101,50个101就等于5050了.高斯算法将加法问题转化为乘法运算,迅速准确得到了结果.
学了之后你会发现你比高斯聪明
2.2.2 等差数列的前n项和
教学目标
知识与能力
(1)掌握等差数列前n项和公式.
(2)掌握等差数列前n项和公式的推导过程.
(3)会简单运用等差数列的前n项和公式.
过程与方法
(1)通过对等差数列前n项和公式的推导过程,渗透倒序相加求和的数学方法.
(2)通过公式的运用体会方程的思想.
(3)通过运用公式的过程,提高学生类比化归、数形结合的能力.
情感态度与价值观
结合具体模型,将教材知识和实际生活联系起来,使学生感受数学的实用性,有效激发学习兴趣,并通过对等差数列求和历史的了解,渗透数学史和数学文化.
教学重难点
重点:
等差数列前n项和的公式,有关等差数列问题求解的基本方法.
难点:
获得递推公式的思路,等差数列前n项和公式的其他形式.
思考:图案中,第1层到第21层一共有多少颗宝石?用什么办法做呢?
这是求奇数个项的和的问题,能不能直接用高斯的办法呢求和呢?
问题:图案中,第1层到第21层一共有多少颗宝石?
倒过来相加如何?
21
21
20
19
1
1
2
3
获得算法:
设等差数列 {an} 的首项为a1,公差为d,如何求等差数列的前n项和Sn= a1 +a2+a3+…+an?
设等差数列a1,a2,a3,…
它的前n 项和是 Sn=a1+a2+…+an-1+an (1)
若把次序颠倒是 Sn=an+an-1+…+a2+a1 (2)
由等差数列的性质 a1+an=a2+an-1=a3+an-2=…
例 1:
解:
(1)(2)两式左右分别相加,得
这种方法叫倒序相加法.
2Sn=(a1+an)+ (a2+an-1)+ (a3+an-2)+…+
(an-2+a3)+ (an-1+a2)+ (an+a1)=n(a1+an)
能否用a1,n,d表示Sn呢?
将an=a1+(n-1)d代入
【说明】
①推导等差数列的前n项和公式的方法叫 ;
②{an}为等差数列? ,这是一个关于 的,没有 的“ ” .
倒序相加法
Sn=an2+bn
n
常数项
二次函数
( 注意 a 还可以是 0)
等差数列前n项和公式
【公式记忆】
用梯形面积公式记忆等差数列前n项和公式,这里对图形进行了割、补两种处理,对应着等差数列前n项和的两个公式.
等差数列的前n项和公式类同于 ;
梯形的面积公式
(补成平行四边形)
a1
a1
an
an
__
__
n
__
__
n
a1
a1
(n-1)d
(分割成一个平行四边形及一个三角形)
1、若数列{an}为等差数列,则s3m=3(s2m-sm)
2、若数列{an}为等差数列,且sp=q,sq=p,sp+q=-(p+q)
3、若数列项数为2n+1,则s奇+s偶=s2n+1= (a1+a2n+1)×(2n+1),s奇-s偶=an+1,
等差数列前n项和的结论
将等差数列的前n项和公式写成上
述形式,有利于求其前n项和的极值:
等差数列前n项和再认识:
a1<0,d>0 a1>0, d<0
极大值 无 有
极小值 有 无
n
sn
n
sn
a1<0, d>0,极小值
a1>0,d<0,极大值
观察上面的式子,我们可以看出它是关于n 的二次函数,从而等差数列的前n项和可以写成形如:
y = Ax2+ Bx
y = Ax+ B
通过上面的例题,对于等差数列的相关量a1、d、n、an、sn,一般确定几个量就可以确定其他量?
a1、an、n
an、sn
a1、d、an
a1、d、n
a1、an、sn
an、d、n
an、sn、n
n、sn
d、sn
d、n
a1、sn
a1、d
由以上例题可以得出:在求等差数列的前n项的和时,当知道首项和公差,或者是知道首项和末项,均可以得出.
已知等差数列an中a2+a5+a12+a15=36.
求前16项的和?
由等差数列的性质可得:
a1+a16=a2+a15=a5+a12=36/2=18
sn=(16/2 )×18=144
答:前16项的和为144.
分析:可以由等差数列性质,直接代入前n项和公式.
例 2:
解:
等差数列 -10,-6,-2,2,…前多少项的和是54?
解:
n1=9,n2=-3 (舍去)
等差数列-10,-6,-2,2,…前9项的和是54.
例3:
设题中的等差数列为{an},前n项和是 Sn,
则a1= -10,d= -6-(-10) = 4,设 Sn=54,
根据等差数列前 n项和公式,得
n要为正整数
已知一个等差数列的前10项的和是310,前20项的和是1220,求Sn.
解:
S10=310,S20=1 220
例 4:
法二:相减得5d=-110
即 d=-22
一个等差数列,共有 10 项,其中奇数项的和为 125,偶数项的和为 15,求 a 1、d.
例 5:
解:
归纳:
等差数列中,
n 为奇数,必有
n 为偶数,必有
等差数列中,a5=14,a2+ a9=31,求S12
法二:
∵ a 5 + a 6 = a 2 + a 9
∴ a 6 = 17
公差 d = a 6 -a 5 = 3
∴ a 7 = 20
= ( a 6 + a 7 )×6
= 222
例6:
解:
等差数列 { a n } 中,S 15 = 90,求 a 8
法一:a 1 + a 1 + 14d = 12
即 a 1 + a 15 = 12
即 a 1 + 7d = 6
∴ a 8 = a 1 + 7d = 6
= 6
例7:
解:
选用中项求等差数列的前 n 项之和 S n
当 n 为奇数时,S n = ____________;
当 n 为偶数时, S n = _______________________.
归纳:
南北朝时,张丘建始创等差数列求和解法。他在《张丘建算经》里给出了几个等差数列问题.
例如:“今有女子不善织布,逐日所织之布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?”
原书的解法是:“并初、末日织布数,半之,余以乘织讫日数,即得.”
思考与余味:
再如:“今有女子善织布,逐日所织的布以同数递增,初日织五尺,计织三十日,共织九匹三丈,问日增几何?”
这是一道等差数列知道前30项和,a1的值,求等差数列的公差.
课堂小结
本节课主要讲述了等差数列的前n项和公式:
① s n=n(a1+an)/2
② s n=na1+n(n-1)d/2
以及他们的推导过程,在具体使用时,不一定完全套用公式,要灵活变通.
③
1.推导等差数列前 n项和公式的方法.
2.公式的应用中的数学思想.
-------倒序相加法
-------方程思想
3.公式中五个量a1, d, an, n, sn, 已知
其中三个量,可以求其余两个.
-------知三求二
裂项求和
有些数列求和的问题,可以对相应的数列的通项公式加以变形,将其写成两项的差,这样整个数列求和的各加数都按同样的方法裂成两项之差,其中每项的被减数一定是后面某项的减数,从而经过逐项相消仅剩下有限项,可得出前n项和公式。
?????????????????????????????????????????????????????????????????.
知识要点补充
如求和: ????????????????????????????????????????????????????????????
提示:
则:
随堂练习
1、如图,一个堆放铅笔的 V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多一支,最上面一层放120支.这个V形架上共放着多少支铅笔?
由题意可知,这个V形架上共放着120层铅笔,且自下而上各层的铅笔数成等差数列,记为{an},其中 a1=1 , a120=120.根据等差数列前n项和的公式,得
答:V形架上共放着 7260支铅笔.
解:
2、在等差数列{an}中,
(2)a1=14.5,d=0.7,an=32,求Sn
(1)a3= -2,a8=12,求S10
(2)由等差数列的通项公式,得
14.5+(n-1)?0.7=32 ? n=26
(1)a1+a10 = a3+a8 = 10
解:
3、凸 n 边形各内角成等差数列,公差为 10?,最小内角为 100?,则n等于( )
(A)7 (B)8 (C)9 (D)8或 9
由题意,得 :
解得 n=8 或 n=9
B
(舍)
解:
这位长跑运动员每天的训练量成等差数列,记为{an}, 其中 a1=7500,a7=10500.
根据等差数列前n项和公式,得
答:这位长跑运动员7天共跑了63000m.
4、某长跑运动员7天里每天的训练量是:
7500, 8000 , 8500 , 9000 , 9500 , 10000 ,10500
这位运动员7天共跑了多少米? (单位:m)
解:
