人教B版 必修5 高二数学 2.3.1等比数列 教学课件(共40张PPT)
文档属性
| 名称 | 人教B版 必修5 高二数学 2.3.1等比数列 教学课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 00:00:00 | ||
图片预览










文档简介
(共40张PPT)
回顾旧知
(1)复习数列的有关概念
(2)复习等差数列的有关概念
(3)复习等差数列前n项和的概念
首先对上一节课,进行回顾
世界杂交水稻之父—袁隆平
袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?
学了本节,这样的小问题就如探囊取物?
2.3.1 等比数列
教学目标
(1)理解等比数列的概念,掌握等比数列的通项公式,并能运用公式解决简单的问题.
(2)理解等比数列的概念,能用函数的观点认识等比数列.
知识与能力
过程与方法
(1)通过观察、操作,了解等比数列的过程.
(2)进一步了解等比数列在实际生活中的应用.
(3)掌握简单的等比数列的方法,在动手操作中认识等比数列.
情感态度与价值观
(1)通过对等比数列概念的归纳,进一步培养学生严密的思维习惯,以及实事求是的科学态度.
(2)通过对等比数列的研究,逐步培养学生观察、类比、归纳、猜想等思维品质.
教学重难点
等比数列“等比”特点的理解、把握和应用.
重点:
(1)等比数列的概念的理解与掌握.
(2)等比数列的通项公式的推导及应用.
难点:
(1) 8,16,32,64,128,256,…
(2) 1,1,1,1,1,1,1,…
(3) 243,81,27,9,3,1,,,…
(4) 1,-1,1,-1,1,-1,1,-1,…
(5) 1,-10,100,-1000,10000,100000,…
说出这些数列的特点
想一想
共同特点:从第二项起,第一项与前一项的比都等于同一个常数 .
等比数列:一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,用字母q表示.
等比数列的概念
等比数列的通项公式:
……
递推法
等比数列的通项公式:
……
共n – 1 项
×)
叠乘法
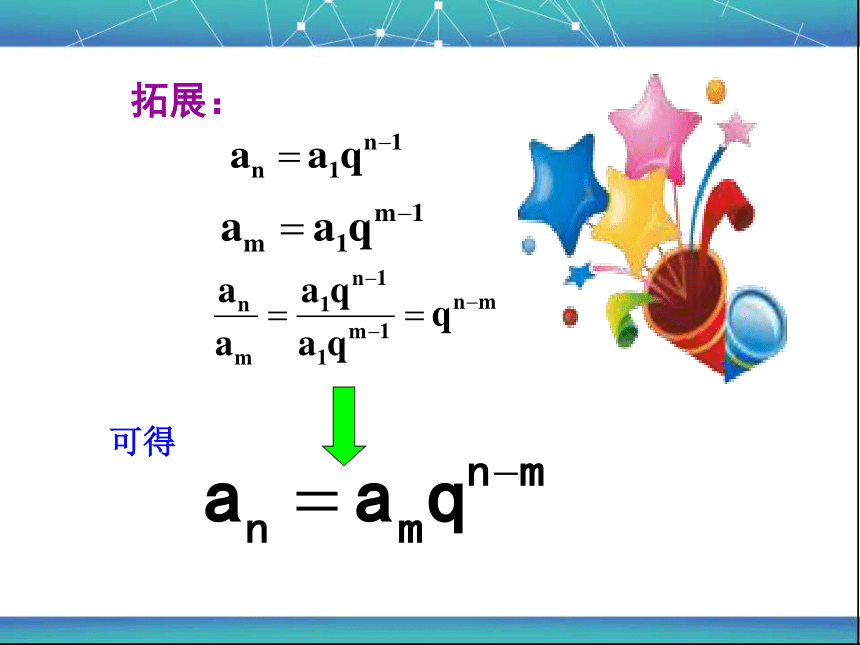
拓展:
可得
等比数列的注意点
(1)等比数列的首项不为0;
(2)等比数列的每一项都不为0,即 ;
(4)公比q一定是由后项除以前项所得,而不能用前项除以后项来求;
(3) q=1时,{an}为常数列;
等比数列的单调性
{an}为递增数列?
或
{an}为递减数列?
或
{an}为摆动数列?
{an}为常数列?
等比数列的等价式
等比中项
如果在a与b中间插入一个数G,使 a、G、b成等比数列,那么G叫做a与b的等比中项.
因此,
如果G是a与b的等比中项,那么
,即
那么G是 的等比中项.
或
反过来,如果 同号,G等于
知识要点
同号的两项才有等比中项,且有两个.
(因为是等比中项的平方)
注意
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
定义变形?
通项公式?
一般形式?
an+1-an=d
d 叫公差
q叫公比
an+1=an+d
an+1=an q
an= a1+(n-1)d
an=a1qn-1
an=am+(n-m)d
an=amqn-m
等差数列与等比数列的对比
已知:a,b,c成等比数列,
求证:ab,ac,bc成等比数列.
证明: 在等比数列
∵ am=a1qm-1 , an=a1 qn-1
∴ aman=a1qn-1a1qm-1=a12qn+m-2
=a12qr+s-2=a1qr-1a1qs-1
=aras
∴aman=aras
例1
已知{an}是公比为q的等比数列,且a1,a3,a2成等差数列,求q.
分析:这是一个等差数列与等比数列结合的题.
a1×a3=a22 a1+a2=2a3
得q=1或
例2
解:
3
10
1
5
2
1
,
,
10
10
10
10
5
1
5
2
5
1
5
0
)这个数列中任意两项的积仍然在这个数列中.
(
项的
项是它后面第
)这个数列中的任意一
(
;
这个数列是等比数列
)
(
求证:
,
,
,
,
已知无穷数列
L
L
-
n
例3
分析:这是等比数列定义与性质的应用.
所以,这个数列是等比数列 .
∵p ,q ? N* ,所以 p + q – 1 ? N*,
已知数列
满足
(1)求证:数列{bn+2}是公比为2的等比数列;
(2)求
例4
分析:此题是两个数列相结合的问题.首先要明白关系.
解:
(1)由 得
是公比为2的等比数列.
令n=1,2,…n-1,则
各式相加得
(2)由(1)可知
(1)观察归纳法 这个方法需要学生很强的反应能力!
比如 21,203,2005,20007…这个你能很快看出来吗 ?
(2)累差法和累商法(我们书本教材上叫做迭加和迭乘,具体前面说了这就不多说了)
形如:已知a1,且an+1-an=f(n) 已知a1,且an+1/an=f(n) .
求等差等比数列通项公式的常用方法
(3)构造法 这个方法最难,不过把握技巧后无论什么题目都是迎刃而解 形如:已知a1,an+1=pan+q的形式就可构造,即配成an+1+x=p(an+x) 当然中间减号也是一样!
例题,数列满足a1=1,an+1=1/2 an+1 解:设an+1+A=1/2(an+A) 然后一零待定系数放,这个展开各项都应等于原题的各项就可以求出了!
(4)公式法 这个方法不用多讲了!两个公式,等差,等比!不用题目往往不会考你那么简单,经常都设置个陷阱,可能是 n=1常常没考虑进去!所以做题时应慎之!
2.
是等比数列
成等差数列时,
成等比数列.
1.
公比为的q等比数列中,
等比数列的解题技巧
结论:a,b同号,G2=ab是G是a,b的 等比中项的充要条件.
3.
5.下标和公式:
等比数列{an}中,如果 m+n=r+s,(m,n,r,s ∈N*) 那么am.an=ar as .
4.对称设法:三数为 a/q,a, aq
.
,
,
,
,
.
,
,
,
.
2
6.
q
aq3
aq
aq
a
注意这里公比是
分别为
并知其积时,可设它们
当四个数成等比数列,
这样便于求解
它们分别为
并知其积时,可设
当三个数成等比数列,
1. 等比数列的概念.必须从第2项起后项除以前项,并且比是 同 一常数.
2.等差数列的通项公式 an=a1qn –1.
知道其中三 个(或两个)字母变量,可用列方程(或方程组)的方法,求余下的一个(或两个)变量.
课堂小结
记一记
3.等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列, 那么G叫做a与b的等比中项.(有两个它们互为相反数)
4.做求等比数列题的一些技巧与方法.
随堂练习
1.在等比数列 { a n } 中,a 1 = 2 ,a 7 a 8 = 80 ,
求 a 14 .
解:因为{ a n }为等比数列 ,所以 a 1a 14 = a 7 a 8 .
2.已知数列
是等差数列,且
(1)求数列
的通项公式;
求数列
前n项和的公式.
(2)令
(1)设数列
公差为
,则
又
所以
(2)令
则由
得
①
解:
②
时,①式减去②式,得
所以
当
时,
综上可得:当
时,
当
时,
当
3.已知数列
满足
(1)求证:数列{bn+2}是公比为2的等比数列;
(2)求 的值。
(1)由
,
是公比为2的等比数列.
令n=1,2,…n-1,则
各式相加得
(2)由(1)可知
解:
4.已知数列
的前n项和为
(1)求
(2)求证数列
是等比数列.
(1)由
得
∴
又
即
得
(2)当n>1时,
得
所以
是首项为
公比为
的等比数列.
解:
回顾旧知
(1)复习数列的有关概念
(2)复习等差数列的有关概念
(3)复习等差数列前n项和的概念
首先对上一节课,进行回顾
世界杂交水稻之父—袁隆平
袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?
学了本节,这样的小问题就如探囊取物?
2.3.1 等比数列
教学目标
(1)理解等比数列的概念,掌握等比数列的通项公式,并能运用公式解决简单的问题.
(2)理解等比数列的概念,能用函数的观点认识等比数列.
知识与能力
过程与方法
(1)通过观察、操作,了解等比数列的过程.
(2)进一步了解等比数列在实际生活中的应用.
(3)掌握简单的等比数列的方法,在动手操作中认识等比数列.
情感态度与价值观
(1)通过对等比数列概念的归纳,进一步培养学生严密的思维习惯,以及实事求是的科学态度.
(2)通过对等比数列的研究,逐步培养学生观察、类比、归纳、猜想等思维品质.
教学重难点
等比数列“等比”特点的理解、把握和应用.
重点:
(1)等比数列的概念的理解与掌握.
(2)等比数列的通项公式的推导及应用.
难点:
(1) 8,16,32,64,128,256,…
(2) 1,1,1,1,1,1,1,…
(3) 243,81,27,9,3,1,,,…
(4) 1,-1,1,-1,1,-1,1,-1,…
(5) 1,-10,100,-1000,10000,100000,…
说出这些数列的特点
想一想
共同特点:从第二项起,第一项与前一项的比都等于同一个常数 .
等比数列:一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,用字母q表示.
等比数列的概念
等比数列的通项公式:
……
递推法
等比数列的通项公式:
……
共n – 1 项
×)
叠乘法
拓展:
可得
等比数列的注意点
(1)等比数列的首项不为0;
(2)等比数列的每一项都不为0,即 ;
(4)公比q一定是由后项除以前项所得,而不能用前项除以后项来求;
(3) q=1时,{an}为常数列;
等比数列的单调性
{an}为递增数列?
或
{an}为递减数列?
或
{an}为摆动数列?
{an}为常数列?
等比数列的等价式
等比中项
如果在a与b中间插入一个数G,使 a、G、b成等比数列,那么G叫做a与b的等比中项.
因此,
如果G是a与b的等比中项,那么
,即
那么G是 的等比中项.
或
反过来,如果 同号,G等于
知识要点
同号的两项才有等比中项,且有两个.
(因为是等比中项的平方)
注意
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
定义变形?
通项公式?
一般形式?
an+1-an=d
d 叫公差
q叫公比
an+1=an+d
an+1=an q
an= a1+(n-1)d
an=a1qn-1
an=am+(n-m)d
an=amqn-m
等差数列与等比数列的对比
已知:a,b,c成等比数列,
求证:ab,ac,bc成等比数列.
证明: 在等比数列
∵ am=a1qm-1 , an=a1 qn-1
∴ aman=a1qn-1a1qm-1=a12qn+m-2
=a12qr+s-2=a1qr-1a1qs-1
=aras
∴aman=aras
例1
已知{an}是公比为q的等比数列,且a1,a3,a2成等差数列,求q.
分析:这是一个等差数列与等比数列结合的题.
a1×a3=a22 a1+a2=2a3
得q=1或
例2
解:
3
10
1
5
2
1
,
,
10
10
10
10
5
1
5
2
5
1
5
0
)这个数列中任意两项的积仍然在这个数列中.
(
项的
项是它后面第
)这个数列中的任意一
(
;
这个数列是等比数列
)
(
求证:
,
,
,
,
已知无穷数列
L
L
-
n
例3
分析:这是等比数列定义与性质的应用.
所以,这个数列是等比数列 .
∵p ,q ? N* ,所以 p + q – 1 ? N*,
已知数列
满足
(1)求证:数列{bn+2}是公比为2的等比数列;
(2)求
例4
分析:此题是两个数列相结合的问题.首先要明白关系.
解:
(1)由 得
是公比为2的等比数列.
令n=1,2,…n-1,则
各式相加得
(2)由(1)可知
(1)观察归纳法 这个方法需要学生很强的反应能力!
比如 21,203,2005,20007…这个你能很快看出来吗 ?
(2)累差法和累商法(我们书本教材上叫做迭加和迭乘,具体前面说了这就不多说了)
形如:已知a1,且an+1-an=f(n) 已知a1,且an+1/an=f(n) .
求等差等比数列通项公式的常用方法
(3)构造法 这个方法最难,不过把握技巧后无论什么题目都是迎刃而解 形如:已知a1,an+1=pan+q的形式就可构造,即配成an+1+x=p(an+x) 当然中间减号也是一样!
例题,数列满足a1=1,an+1=1/2 an+1 解:设an+1+A=1/2(an+A) 然后一零待定系数放,这个展开各项都应等于原题的各项就可以求出了!
(4)公式法 这个方法不用多讲了!两个公式,等差,等比!不用题目往往不会考你那么简单,经常都设置个陷阱,可能是 n=1常常没考虑进去!所以做题时应慎之!
2.
是等比数列
成等差数列时,
成等比数列.
1.
公比为的q等比数列中,
等比数列的解题技巧
结论:a,b同号,G2=ab是G是a,b的 等比中项的充要条件.
3.
5.下标和公式:
等比数列{an}中,如果 m+n=r+s,(m,n,r,s ∈N*) 那么am.an=ar as .
4.对称设法:三数为 a/q,a, aq
.
,
,
,
,
.
,
,
,
.
2
6.
q
aq3
aq
aq
a
注意这里公比是
分别为
并知其积时,可设它们
当四个数成等比数列,
这样便于求解
它们分别为
并知其积时,可设
当三个数成等比数列,
1. 等比数列的概念.必须从第2项起后项除以前项,并且比是 同 一常数.
2.等差数列的通项公式 an=a1qn –1.
知道其中三 个(或两个)字母变量,可用列方程(或方程组)的方法,求余下的一个(或两个)变量.
课堂小结
记一记
3.等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列, 那么G叫做a与b的等比中项.(有两个它们互为相反数)
4.做求等比数列题的一些技巧与方法.
随堂练习
1.在等比数列 { a n } 中,a 1 = 2 ,a 7 a 8 = 80 ,
求 a 14 .
解:因为{ a n }为等比数列 ,所以 a 1a 14 = a 7 a 8 .
2.已知数列
是等差数列,且
(1)求数列
的通项公式;
求数列
前n项和的公式.
(2)令
(1)设数列
公差为
,则
又
所以
(2)令
则由
得
①
解:
②
时,①式减去②式,得
所以
当
时,
综上可得:当
时,
当
时,
当
3.已知数列
满足
(1)求证:数列{bn+2}是公比为2的等比数列;
(2)求 的值。
(1)由
,
是公比为2的等比数列.
令n=1,2,…n-1,则
各式相加得
(2)由(1)可知
解:
4.已知数列
的前n项和为
(1)求
(2)求证数列
是等比数列.
(1)由
得
∴
又
即
得
(2)当n>1时,
得
所以
是首项为
公比为
的等比数列.
解:
