2019秋北师大版九年级数学上册第三章概率的进一步认识复习学案(无答案)
文档属性
| 名称 | 2019秋北师大版九年级数学上册第三章概率的进一步认识复习学案(无答案) | 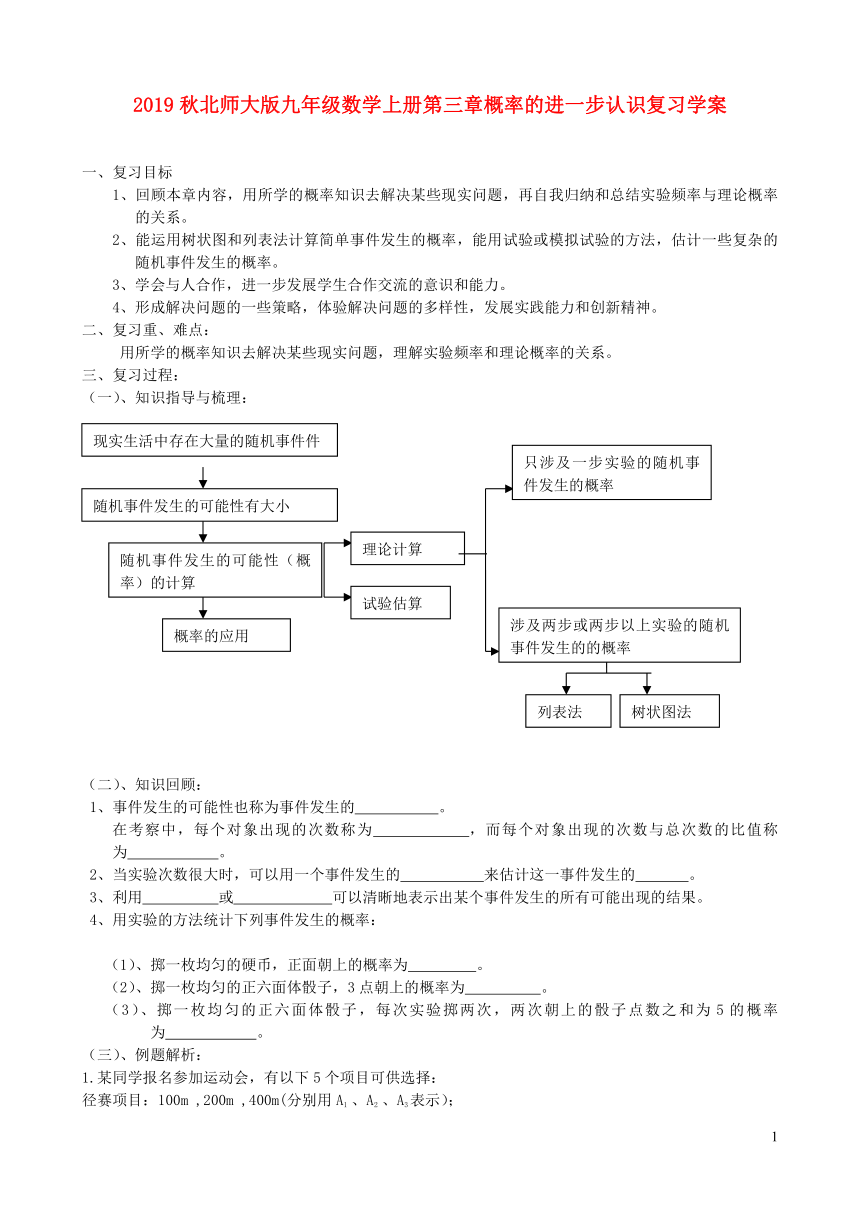 | |
| 格式 | zip | ||
| 文件大小 | 15.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 18:06:12 | ||
图片预览


文档简介
2019秋北师大版九年级数学上册第三章概率的进一步认识复习学案
一、复习目标
1、回顾本章内容,用所学的概率知识去解决某些现实问题,再自我归纳和总结实验频率与理论概率的关系。
2、能运用树状图和列表法计算简单事件发生的概率,能用试验或模拟试验的方法,估计一些复杂的随机事件发生的概率。
3、学会与人合作,进一步发展学生合作交流的意识和能力。
4、形成解决问题的一些策略,体验解决问题的多样性,发展实践能力和创新精神。
二、复习重、难点:
用所学的概率知识去解决某些现实问题,理解实验频率和理论概率的关系。
三、复习过程:
(一)、知识指导与梳理:
(二)、知识回顾:
1、事件发生的可能性也称为事件发生的 。
在考察中,每个对象出现的次数称为 ,而每个对象出现的次数与总次数的比值称为 。
2、当实验次数很大时,可以用一个事件发生的 来估计这一事件发生的 。
3、利用 或 可以清晰地表示出某个事件发生的所有可能出现的结果。
4、用实验的方法统计下列事件发生的概率:
(1)、掷一枚均匀的硬币,正面朝上的概率为 。
(2)、掷一枚均匀的正六面体骰子,3点朝上的概率为 。
(3)、掷一枚均匀的正六面体骰子,每次实验掷两次,两次朝上的骰子点数之和为5的概率为 。
(三)、例题解析:
1.某同学报名参加运动会,有以下5个项目可供选择:
径赛项目:100m ,200m ,400m(分别用A1 、A2 、A3表示);
田赛项目:跳远 ,跳高(分别用B1 、B2表示).
⑴ 该同学从5个项目中任选一个,恰好是田赛项目的概率为 ;
⑵ 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
2.小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小明胜,否则,小军胜.
(1)请用树形图或列表法列出摸笔游戏所有可能的结果;
(2)请计算小明获胜的概率,并指出本游戏规则是否公平,若不公平,你认为对谁有利
(四):当堂检测
1、从其中含有4个次品的1000个螺钉中任取1个,它是次品的概率是 。
2、在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红球,两个黄球。如果第一次先从口袋中摸出一球后,不再放回,第二次再从口袋中摸出一球,那么两次都摸到黄球的概率是 。
3、为了估计湖里有多少条鱼,有如下方案:从湖里捕上100条做上标记,然后放回湖里去,经过一段时间,待带标记的鱼完全混合于鱼群后,第二次再捕上200条,若其中带标记的鱼有25条,那么湖里大约有 条鱼。
4、三个人站成一排,通过实验可得,甲站在中间的概率为( )
A、 B、 C、 D、
5.一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是 .
6、如图6所示的两个圆盘中,指针居在每个数上的机会均等,那么两个指针同时落在偶数上的概率是( )
A、 B、 C、 D、
7、小明的衣柜里有两件上衣,一件是长袖的,一件是短袖的;有三条裤子,分别为白色、黄色、蓝色,他任意拿出一件上衣和一条裤子,正好是长袖上衣和白色裤子的概率是( )
A、 B、 C、 D、
8、某商店举办有奖销售活动,办法如下:凡购物满100元者得奖券一张,多购多得,每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率应该是( )
A、 B、 C、 D、
9. (2014?江苏徐州,第23题8分)某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
10. 在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点(x,y)在函数y=﹣x+5图象上的概率.
一、复习目标
1、回顾本章内容,用所学的概率知识去解决某些现实问题,再自我归纳和总结实验频率与理论概率的关系。
2、能运用树状图和列表法计算简单事件发生的概率,能用试验或模拟试验的方法,估计一些复杂的随机事件发生的概率。
3、学会与人合作,进一步发展学生合作交流的意识和能力。
4、形成解决问题的一些策略,体验解决问题的多样性,发展实践能力和创新精神。
二、复习重、难点:
用所学的概率知识去解决某些现实问题,理解实验频率和理论概率的关系。
三、复习过程:
(一)、知识指导与梳理:
(二)、知识回顾:
1、事件发生的可能性也称为事件发生的 。
在考察中,每个对象出现的次数称为 ,而每个对象出现的次数与总次数的比值称为 。
2、当实验次数很大时,可以用一个事件发生的 来估计这一事件发生的 。
3、利用 或 可以清晰地表示出某个事件发生的所有可能出现的结果。
4、用实验的方法统计下列事件发生的概率:
(1)、掷一枚均匀的硬币,正面朝上的概率为 。
(2)、掷一枚均匀的正六面体骰子,3点朝上的概率为 。
(3)、掷一枚均匀的正六面体骰子,每次实验掷两次,两次朝上的骰子点数之和为5的概率为 。
(三)、例题解析:
1.某同学报名参加运动会,有以下5个项目可供选择:
径赛项目:100m ,200m ,400m(分别用A1 、A2 、A3表示);
田赛项目:跳远 ,跳高(分别用B1 、B2表示).
⑴ 该同学从5个项目中任选一个,恰好是田赛项目的概率为 ;
⑵ 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
2.小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小明胜,否则,小军胜.
(1)请用树形图或列表法列出摸笔游戏所有可能的结果;
(2)请计算小明获胜的概率,并指出本游戏规则是否公平,若不公平,你认为对谁有利
(四):当堂检测
1、从其中含有4个次品的1000个螺钉中任取1个,它是次品的概率是 。
2、在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红球,两个黄球。如果第一次先从口袋中摸出一球后,不再放回,第二次再从口袋中摸出一球,那么两次都摸到黄球的概率是 。
3、为了估计湖里有多少条鱼,有如下方案:从湖里捕上100条做上标记,然后放回湖里去,经过一段时间,待带标记的鱼完全混合于鱼群后,第二次再捕上200条,若其中带标记的鱼有25条,那么湖里大约有 条鱼。
4、三个人站成一排,通过实验可得,甲站在中间的概率为( )
A、 B、 C、 D、
5.一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是 .
6、如图6所示的两个圆盘中,指针居在每个数上的机会均等,那么两个指针同时落在偶数上的概率是( )
A、 B、 C、 D、
7、小明的衣柜里有两件上衣,一件是长袖的,一件是短袖的;有三条裤子,分别为白色、黄色、蓝色,他任意拿出一件上衣和一条裤子,正好是长袖上衣和白色裤子的概率是( )
A、 B、 C、 D、
8、某商店举办有奖销售活动,办法如下:凡购物满100元者得奖券一张,多购多得,每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率应该是( )
A、 B、 C、 D、
9. (2014?江苏徐州,第23题8分)某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
10. 在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点(x,y)在函数y=﹣x+5图象上的概率.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
