苏科版九年级数学下册 6.6“相似三角形的性质”、“图形的位似”自测题(含答案)
文档属性
| 名称 | 苏科版九年级数学下册 6.6“相似三角形的性质”、“图形的位似”自测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 177.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 20:41:48 | ||
图片预览

文档简介
“相似三角形的性质”、“图形的位似”自测题
基础闯关
(时间:45 分钟;满分:100 分) 一、选择题(每小题 4 分,共 20 分)
如图 1, ? ABC∽ ? ADB,下列关系成立的是( ).
A. ? ADB= ? ACB B. ? ADB= ? ABC
C. ? CDB= ? CAB D. ? ABC= ? BDC
如图 2,在? ABC 中,DE//BC,AD=3,BD=2,EC=1,那么 AE 等于( ).
A.3 B.2 C.1.5 D.1
如图 3,在平行四边形 ABCD 中,点 E 在边 BC 上,BE:EC=2:3,连接 AE,交 BD
于点 F,则△BFE 的面积与△DFA 的面积之比为( ).
A.2:3 B.4:9 C.2:5 D.4:25
图 2 图 3
图 4
下列说法正确的是( ).
A.两个等腰三角形一定是位似图形B.全等图形一定是位似图形
C.位似图形对应顶点的连线一定不在同一直线上D.位似图形一定是相似的几何图形
如图 4,线段 AB 两个端点的坐标分别为 A(6,6),B(8,2),以原点 O 为位似中心,
1
在第一象限内将线段 AB 缩小为原来的
2
后得到线段 CD,则端点 C 的坐标为( ).
A.(3,3) B.(4,3) C.(3,1) D.(4,1) 二、填空题(每小题 4 分,共 32 分)
两个相似三角形的周长比是 4:9,则这两个三角形的相似比是 .
已知△ABC 与△DEF 相似且对应高的比为 2:3,则△ABC 与△DEF 的周长比为
.
AD
如图 5,已知 DE//BC,且
DB
? 1 ,那么? ADE 与? ABC 的面积比等于 .
2
(
图
1
)如图 6,在△ABC 中,DE//AB,CD:DA=2:3,DE=4,则 AB 的长为 .
图 5 图 6
两个相似三角形的一组对应边长分别为 3cm 和 5cm,且较小三角形的周长为 15cm,那么较大三角形的周长为 cm.
若 O 为△ABC 的重心,△BOC 的面积为 4,则△ABC 的面积为 .
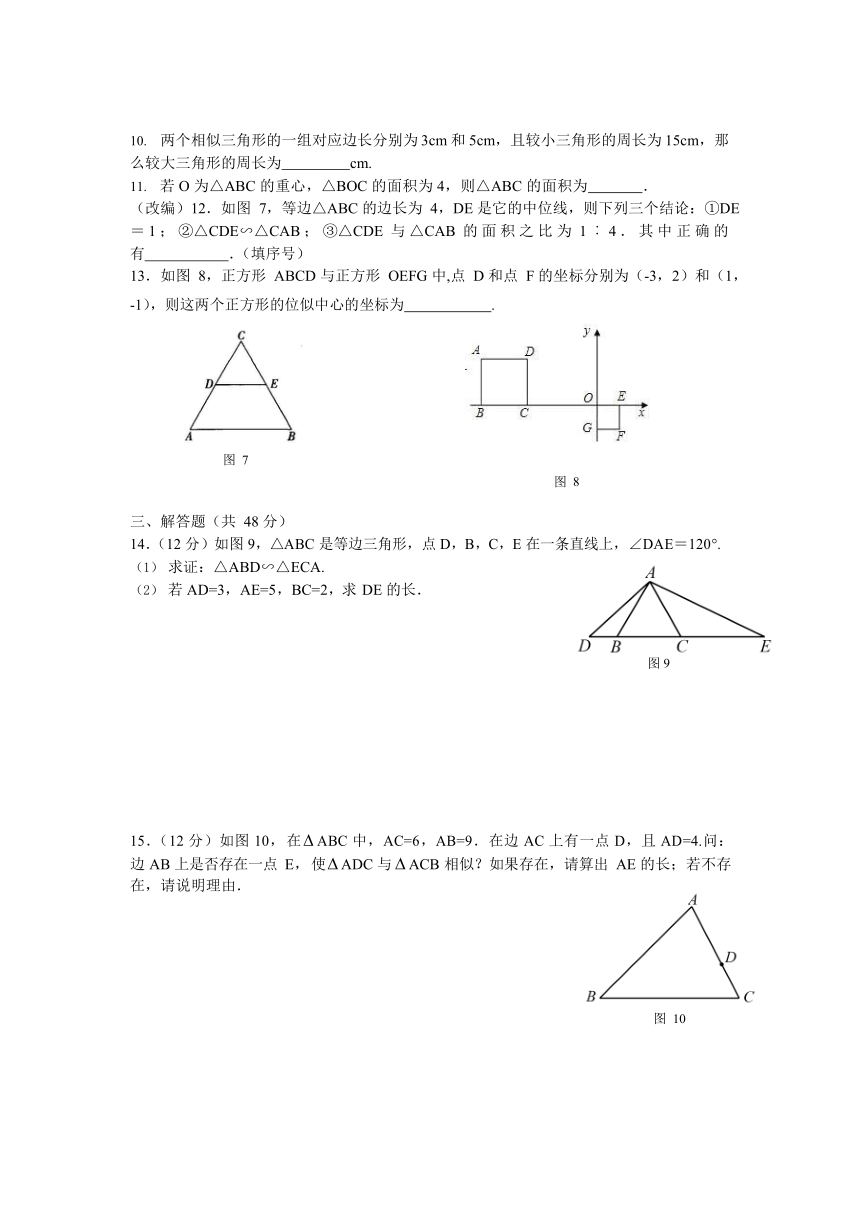
(改编)12.如图 7,等边△ABC 的边长为 4,DE 是它的中位线,则下列三个结论:①DE
= 1 ; ②△CDE∽△CAB ; ③△CDE 与△CAB 的面积 之比为 1 ︰ 4 . 其中 正确的有 .(填序号)
13.如图 8,正方形 ABCD 与正方形 OEFG 中,点 D 和点 F 的坐标分别为(-3,2)和(1,
-1),则这两个正方形的位似中心的坐标为 .
图 7
图 8
三、解答题(共 48 分)
14.(12 分)如图 9,△ABC 是等边三角形,点 D,B,C,E 在一条直线上,∠DAE=120°.
(
图
9
)求证:△ABD∽△ECA.
若 AD=3,AE=5,BC=2,求 DE 的长.
15.(12 分)如图 10,在? ABC 中,AC=6,AB=9.在边 AC 上有一点 D,且 AD=4.问:边 AB 上是否存在一点 E,使? ADC 与? ACB 相似?如果存在,请算出 AE 的长;若不存在,请说明理由.
图 10
16.(12 分)如图 11,在平面直角坐标系中,△OAB 的顶点坐标分别为 O(0,0),A(5,4),B(3,0),分别将点 A,B 的横坐标、纵坐标都乘 2.得到相应的点 A'B'坐标.
画△OA'B'.
△OA'B'与△OAB 是位似形吗?为什么?
17.(12 分)如图 12,四边形 ABCD 为平行四边形,以 CD 为直径作⊙O,⊙O 与边 BC 相交于点 F,⊙O 的切线 DE 与边 AB 相交于点 E,且 AE=3EB.
求证:△ADE∽△CDF.
当 CF︰FB=1︰2 时,求⊙O 与平行四边形 ABCD
的面积之比.
图 11
图 12
能力挑战
(满分:30 分)
1.(5 分)如图 1,△ABC∽△DBA,D 为 BC 上一点,E,F 分别是 AC,AD 的中点,且 AB
(
?
)BE
=28cm,BC=36cm,则 ( ).
BF
4 5 8 9
B. C. D.
(
图
1
)3 3 5 7
图 2
2.(5 分)如图 2,在梯形 ABCD 中,AD∥BC,BE 平分∠ABC 交 CD 于 E,且 BE⊥CD, CE︰ED=2︰1.如果△BEC 的面积为 8,那么四边形 ABED 的面积是 .
3.(5 分)如图 4,在平面直角坐标系内,已知点 A(0,6),点 B(8,0)动点P 从点A 开始在线段AO 上以每秒 1 个单位长度的速度向点O 移动同时动点 Q 从点 B 开始在线段 BA 上以每秒 2 个单位长度的速度向点 A
移动,设点 P,Q 移动的时间为 t 秒.当 t= 秒时,△APQ 的面积
24
为 个平方单位. 图 4
5
4.(15 分)如图 5,在 Rt△ABC 中,∠BAC=90°,AB=AC=
2,点 D 在 BC 上运动(不能到达 B、C),过点 D 作∠ADE=45° DE 交 AC 于 E.
求证:△ABD∽△DCE.
设 BD=x,AE=y,试用含有 x 的代数式表示 y. 图 5
当△ADE 是等腰三角形时,求 AE 的长.
参考答案
基础闯关
1. B 2. C 3. D 4. D 5. A 6. 4︰9 7. 2︰3 8. 1︰9 9. 10 10. 25
11. 12 12. ②③ 13. (-1,0)或(5,-2)
14.(1)略. (2)7.5.提示:可证△EAC∽△EDA.
若△ADE∽△ACB,则
AD ? AE ? 4 ? AE
? AE ? 6 ;若△ADE∽△ABC,则
AC AB 6 9
AD ? AE
? 4 ? AE
? AE ? 8 .
AB AC 9 6 3
图略,△OA'B'与△OAB 是位似图形.
17.(1)∵CD 是⊙O 的直径,∴∠DFC=90°.∵四边形 ABCD 是平行四边形,∴∠A=∠C,
AD∥BC,∴∠ADF=∠DFC=90°.∵DE 为⊙O 的切线,∴DE⊥DC,∴∠EDC=90°,∴∠ADF=
∠EDC=90°,∴∠ADE=∠CDF.∵∠A=∠C,∴△ADE∽△CDE.
∵CF︰FB=1︰2,∴设 CF=x,FB=2x,则 BC=3x.∵AE=3EB,设 EB=y,则 AE=3y, AB=4y.∵四边形 ABCD 是平行四边形,∴AD=BC=3x,AB=DC=4y.∵△ADE∽△CDF,∴
= ,∴ = .∵x,y 均为正数,∴x=2y,∴BC=6y,CF=2y,在 Rt△DFC 中,∠DFC=90°, 由勾股定理得DF===2 y,∴⊙O 的面积为π?(DC) 2= π?DC2= π(4y)2=4πy2,四边形 ABCD 的面积为 BC?DF=6y?2 y=12 y2,∴⊙O 与四边形 ABCD 的面积之比为 4πy2︰12y2=π︰3 .
能力挑战
(
2
)1. D 2. 1 3. 2 或 3
4(.
AB
1)略.(2)∵△ABD∽△DCE,∴
DC
? BD .∵AB=2,BD=x,AE=y ∴ DC ? 2
CE
x ,
EC ? 2 ? y ,∴
2
2
2 ? x
? x
2 ? y
,∴ y ? 1 x 2 ?
2
2x ? 2 .
①若 AD=AE,则∠AED=∠ADE,∴∠DAE= 900 ,此时 D 点与 B 点重合,不符题意;
② 若 AD=DE , 则 ?ABD ? ?DCE
, ∴ CD ? BA ? 2 , ∴
BD ? CE ? 2 ? 2 , ∴
(
2
) (
2
) (
2
)AE ? 2 ? (2 ? 2) ? 4 ? 2 ; ③ 若 AE=DE , 则 ∠ DAE= ∠ ADE=
1
450 , ∴
AD ? BC, DE ? AC, ∴ AE ? CE ?
AC ? 1.综上,当△ADE 是等腰三角形时,AE 的长
2
(
2
)为 4 ? 2
或1.
基础闯关
(时间:45 分钟;满分:100 分) 一、选择题(每小题 4 分,共 20 分)
如图 1, ? ABC∽ ? ADB,下列关系成立的是( ).
A. ? ADB= ? ACB B. ? ADB= ? ABC
C. ? CDB= ? CAB D. ? ABC= ? BDC
如图 2,在? ABC 中,DE//BC,AD=3,BD=2,EC=1,那么 AE 等于( ).
A.3 B.2 C.1.5 D.1
如图 3,在平行四边形 ABCD 中,点 E 在边 BC 上,BE:EC=2:3,连接 AE,交 BD
于点 F,则△BFE 的面积与△DFA 的面积之比为( ).
A.2:3 B.4:9 C.2:5 D.4:25
图 2 图 3
图 4
下列说法正确的是( ).
A.两个等腰三角形一定是位似图形B.全等图形一定是位似图形
C.位似图形对应顶点的连线一定不在同一直线上D.位似图形一定是相似的几何图形
如图 4,线段 AB 两个端点的坐标分别为 A(6,6),B(8,2),以原点 O 为位似中心,
1
在第一象限内将线段 AB 缩小为原来的
2
后得到线段 CD,则端点 C 的坐标为( ).
A.(3,3) B.(4,3) C.(3,1) D.(4,1) 二、填空题(每小题 4 分,共 32 分)
两个相似三角形的周长比是 4:9,则这两个三角形的相似比是 .
已知△ABC 与△DEF 相似且对应高的比为 2:3,则△ABC 与△DEF 的周长比为
.
AD
如图 5,已知 DE//BC,且
DB
? 1 ,那么? ADE 与? ABC 的面积比等于 .
2
(
图
1
)如图 6,在△ABC 中,DE//AB,CD:DA=2:3,DE=4,则 AB 的长为 .
图 5 图 6
两个相似三角形的一组对应边长分别为 3cm 和 5cm,且较小三角形的周长为 15cm,那么较大三角形的周长为 cm.
若 O 为△ABC 的重心,△BOC 的面积为 4,则△ABC 的面积为 .
(改编)12.如图 7,等边△ABC 的边长为 4,DE 是它的中位线,则下列三个结论:①DE
= 1 ; ②△CDE∽△CAB ; ③△CDE 与△CAB 的面积 之比为 1 ︰ 4 . 其中 正确的有 .(填序号)
13.如图 8,正方形 ABCD 与正方形 OEFG 中,点 D 和点 F 的坐标分别为(-3,2)和(1,
-1),则这两个正方形的位似中心的坐标为 .
图 7
图 8
三、解答题(共 48 分)
14.(12 分)如图 9,△ABC 是等边三角形,点 D,B,C,E 在一条直线上,∠DAE=120°.
(
图
9
)求证:△ABD∽△ECA.
若 AD=3,AE=5,BC=2,求 DE 的长.
15.(12 分)如图 10,在? ABC 中,AC=6,AB=9.在边 AC 上有一点 D,且 AD=4.问:边 AB 上是否存在一点 E,使? ADC 与? ACB 相似?如果存在,请算出 AE 的长;若不存在,请说明理由.
图 10
16.(12 分)如图 11,在平面直角坐标系中,△OAB 的顶点坐标分别为 O(0,0),A(5,4),B(3,0),分别将点 A,B 的横坐标、纵坐标都乘 2.得到相应的点 A'B'坐标.
画△OA'B'.
△OA'B'与△OAB 是位似形吗?为什么?
17.(12 分)如图 12,四边形 ABCD 为平行四边形,以 CD 为直径作⊙O,⊙O 与边 BC 相交于点 F,⊙O 的切线 DE 与边 AB 相交于点 E,且 AE=3EB.
求证:△ADE∽△CDF.
当 CF︰FB=1︰2 时,求⊙O 与平行四边形 ABCD
的面积之比.
图 11
图 12
能力挑战
(满分:30 分)
1.(5 分)如图 1,△ABC∽△DBA,D 为 BC 上一点,E,F 分别是 AC,AD 的中点,且 AB
(
?
)BE
=28cm,BC=36cm,则 ( ).
BF
4 5 8 9
B. C. D.
(
图
1
)3 3 5 7
图 2
2.(5 分)如图 2,在梯形 ABCD 中,AD∥BC,BE 平分∠ABC 交 CD 于 E,且 BE⊥CD, CE︰ED=2︰1.如果△BEC 的面积为 8,那么四边形 ABED 的面积是 .
3.(5 分)如图 4,在平面直角坐标系内,已知点 A(0,6),点 B(8,0)动点P 从点A 开始在线段AO 上以每秒 1 个单位长度的速度向点O 移动同时动点 Q 从点 B 开始在线段 BA 上以每秒 2 个单位长度的速度向点 A
移动,设点 P,Q 移动的时间为 t 秒.当 t= 秒时,△APQ 的面积
24
为 个平方单位. 图 4
5
4.(15 分)如图 5,在 Rt△ABC 中,∠BAC=90°,AB=AC=
2,点 D 在 BC 上运动(不能到达 B、C),过点 D 作∠ADE=45° DE 交 AC 于 E.
求证:△ABD∽△DCE.
设 BD=x,AE=y,试用含有 x 的代数式表示 y. 图 5
当△ADE 是等腰三角形时,求 AE 的长.
参考答案
基础闯关
1. B 2. C 3. D 4. D 5. A 6. 4︰9 7. 2︰3 8. 1︰9 9. 10 10. 25
11. 12 12. ②③ 13. (-1,0)或(5,-2)
14.(1)略. (2)7.5.提示:可证△EAC∽△EDA.
若△ADE∽△ACB,则
AD ? AE ? 4 ? AE
? AE ? 6 ;若△ADE∽△ABC,则
AC AB 6 9
AD ? AE
? 4 ? AE
? AE ? 8 .
AB AC 9 6 3
图略,△OA'B'与△OAB 是位似图形.
17.(1)∵CD 是⊙O 的直径,∴∠DFC=90°.∵四边形 ABCD 是平行四边形,∴∠A=∠C,
AD∥BC,∴∠ADF=∠DFC=90°.∵DE 为⊙O 的切线,∴DE⊥DC,∴∠EDC=90°,∴∠ADF=
∠EDC=90°,∴∠ADE=∠CDF.∵∠A=∠C,∴△ADE∽△CDE.
∵CF︰FB=1︰2,∴设 CF=x,FB=2x,则 BC=3x.∵AE=3EB,设 EB=y,则 AE=3y, AB=4y.∵四边形 ABCD 是平行四边形,∴AD=BC=3x,AB=DC=4y.∵△ADE∽△CDF,∴
= ,∴ = .∵x,y 均为正数,∴x=2y,∴BC=6y,CF=2y,在 Rt△DFC 中,∠DFC=90°, 由勾股定理得DF===2 y,∴⊙O 的面积为π?(DC) 2= π?DC2= π(4y)2=4πy2,四边形 ABCD 的面积为 BC?DF=6y?2 y=12 y2,∴⊙O 与四边形 ABCD 的面积之比为 4πy2︰12y2=π︰3 .
能力挑战
(
2
)1. D 2. 1 3. 2 或 3
4(.
AB
1)略.(2)∵△ABD∽△DCE,∴
DC
? BD .∵AB=2,BD=x,AE=y ∴ DC ? 2
CE
x ,
EC ? 2 ? y ,∴
2
2
2 ? x
? x
2 ? y
,∴ y ? 1 x 2 ?
2
2x ? 2 .
①若 AD=AE,则∠AED=∠ADE,∴∠DAE= 900 ,此时 D 点与 B 点重合,不符题意;
② 若 AD=DE , 则 ?ABD ? ?DCE
, ∴ CD ? BA ? 2 , ∴
BD ? CE ? 2 ? 2 , ∴
(
2
) (
2
) (
2
)AE ? 2 ? (2 ? 2) ? 4 ? 2 ; ③ 若 AE=DE , 则 ∠ DAE= ∠ ADE=
1
450 , ∴
AD ? BC, DE ? AC, ∴ AE ? CE ?
AC ? 1.综上,当△ADE 是等腰三角形时,AE 的长
2
(
2
)为 4 ? 2
或1.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
