苏科版九年级下册:6.7“用相似三角形解决问题”同步测试题(含答案)
文档属性
| 名称 | 苏科版九年级下册:6.7“用相似三角形解决问题”同步测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 151.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 22:48:21 | ||
图片预览

文档简介
“用相似三角形解决问题”测试题
基础闯关
(时间:45 分钟;满分:100 分) 一、选择题(每小题 4 分,共 20 分)
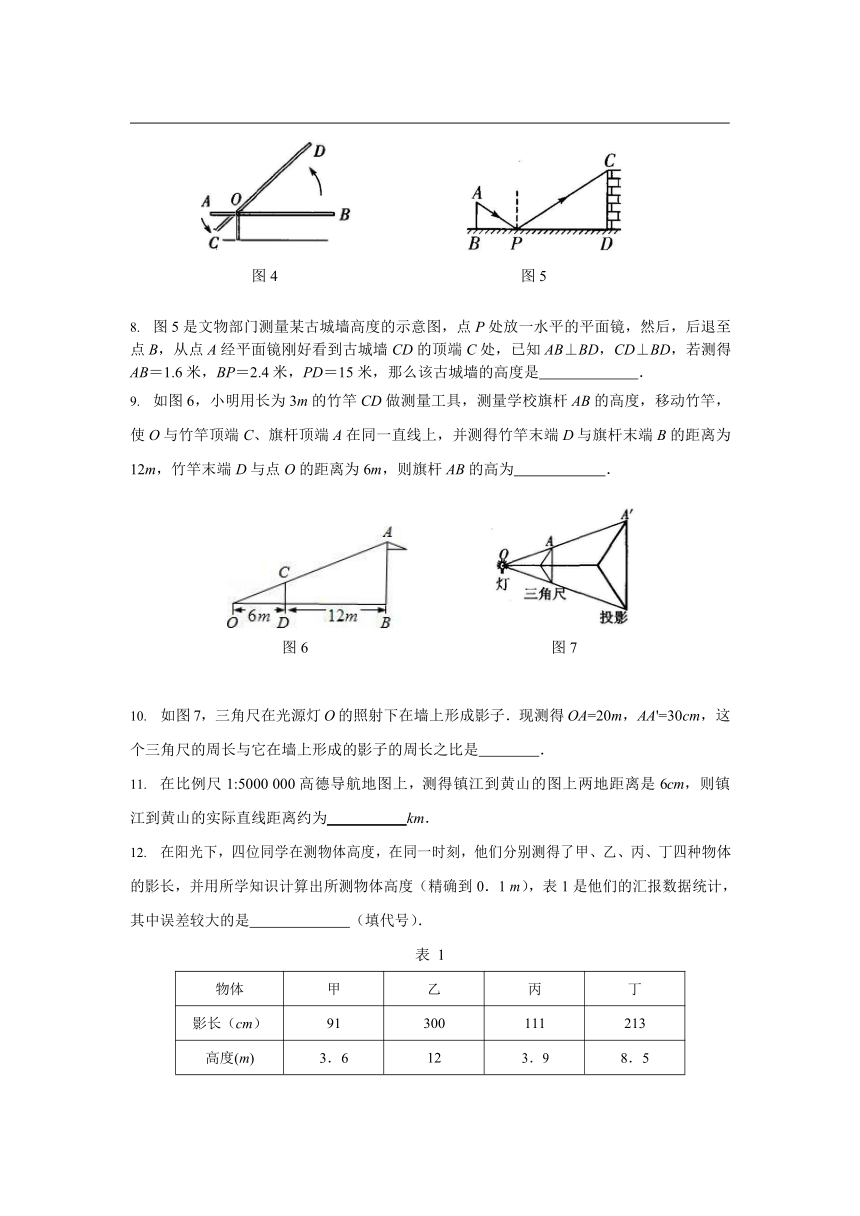
在下面的图形中,表示两棵小树在同一时刻阳光下的影子的是( ).
如图 1,小强晚上在路灯下沿路 AB 散步,在由 A 处走到 B 处这一过程中,他在地上的影子( ).
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
在阳光下,小明测得身高 160cm 小强的影子长是 120cm,在同一时刻,身高 164cm 的小明的影子长是( ).
A.121 cm B.122 cm C.123 cm D.124 cm
小明在市民广场玩耍,他发现,在甲处路灯光照下,小华身体的影子顶部恰好落在乙处,影长 5 块地砖宽距离,小明又数得乙处到甲处路灯之间正好有 30 块地砖(如图 2).已知小华的身高为 150cm,小明很快算得路灯甲的高度为( ).
A.9m B.8m C.750cm D.800cm
图 1 图 2 图 3
幻灯机的工作原理如图 3 所示,已知光源到幻灯片的距离是 30cm,要使幻灯片上 10 cm
高的小树,在屏幕上投影高度至少达 60 cm,则幻灯片到屏幕的距离必须( ).
A.不大于 1.5 m B.不小于 1.5 m C.不大于 1.8m D.不小于 1.8 m
二、填空题(每小题 4 分,共 32 分)
在阳光下身高 1.6 米的小强的影长为 0.8 米,在同一时刻,他测得一棵树的影长为 1.6 米,则这棵树的高度为 米.
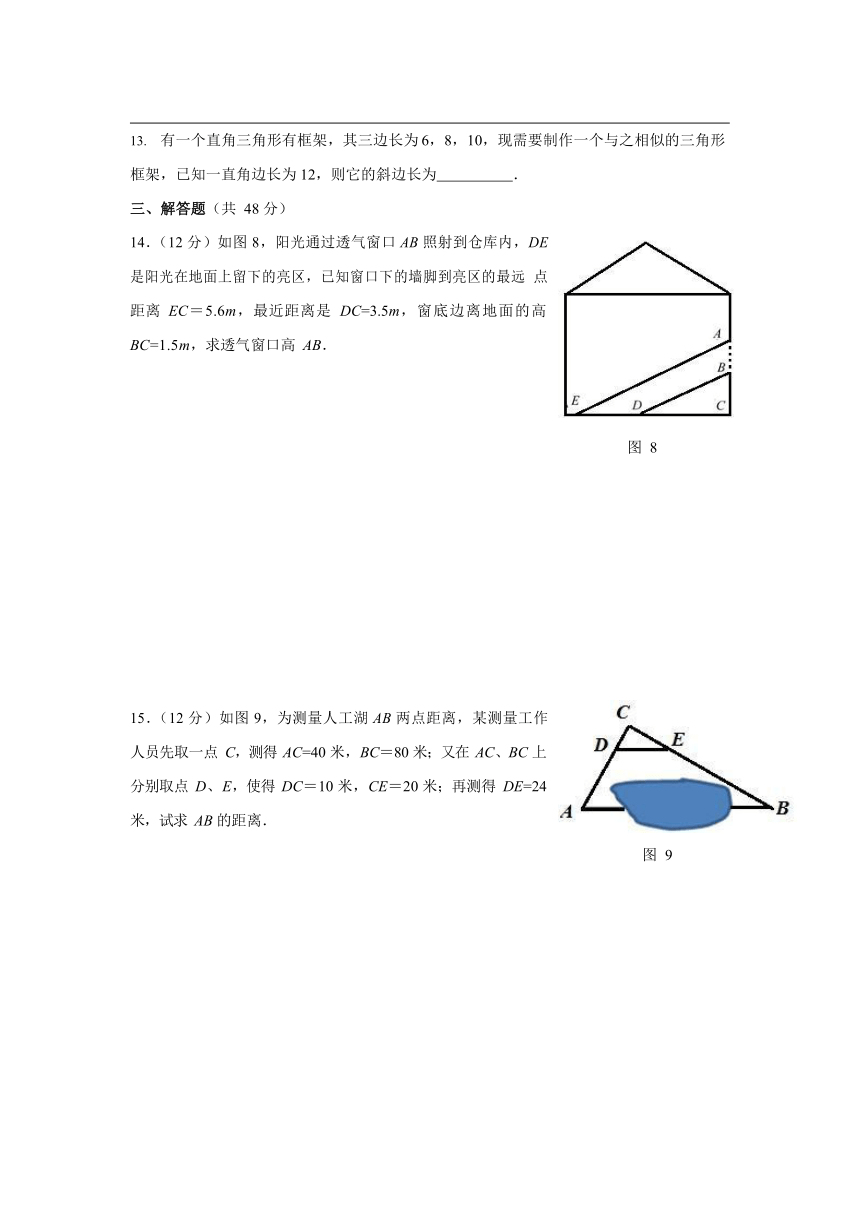
如图 4,铁道口拦挡杆的短臂长 20 厘米,长臂长 16 米,当短臂的端点 A 下降 15 厘米时,长臂的端点 B 升高了(拦挡杆的宽度忽略不计) .
图 4 图 5
图 5 是文物部门测量某古城墙高度的示意图,点 P 处放一水平的平面镜,然后,后退至点 B,从点 A 经平面镜刚好看到古城墙 CD 的顶端 C 处,已知 AB⊥BD,CD⊥BD,若测得AB=1.6 米,BP=2.4 米,PD=15 米,那么该古城墙的高度是 .
如图 6,小明用长为 3m 的竹竿 CD 做测量工具,测量学校旗杆 AB 的高度,移动竹竿, 使 O 与竹竿顶端 C、旗杆顶端 A 在同一直线上,并测得竹竿末端 D 与旗杆末端 B 的距离为12m,竹竿末端 D 与点 O 的距离为 6m,则旗杆 AB 的高为 .
图 6 图 7
如图 7,三角尺在光源灯 O 的照射下在墙上形成影子.现测得 OA=20m,AA'=30cm,这个三角尺的周长与它在墙上形成的影子的周长之比是 .
在比例尺 1:5000 000 高德导航地图上,测得镇江到黄山的图上两地距离是 6cm,则镇江到黄山的实际直线距离约为 km.
在阳光下,四位同学在测物体高度,在同一时刻,他们分别测得了甲、乙、丙、丁四种物体的影长,并用所学知识计算出所测物体高度(精确到 0.1 m),表 1 是他们的汇报数据统计,其中误差较大的是 (填代号).
表 1
物体 甲 乙 丙 丁
影长(cm) 91 300 111 213
高度(m) 3.6 12 3.9 8.5
有一个直角三角形有框架,其三边长为 6,8,10,现需要制作一个与之相似的三角形框架,已知一直角边长为 12,则它的斜边长为 .
三、解答题(共 48 分)
14.(12 分)如图 8,阳光通过透气窗口 AB 照射到仓库内,DE是阳光在地面上留下的亮区,已知窗口下的墙脚到亮区的最远 点距离 EC=5.6m,最近距离是 DC=3.5m,窗底边离地面的高BC=1.5m,求透气窗口高 AB.
图 8
15.(12 分)如图 9,为测量人工湖 AB 两点距离,某测量工作人员先取一点 C,测得 AC=40 米,BC=80 米;又在 AC、BC 上分别取点 D、E,使得 DC=10 米,CE=20 米;再测得 DE=24 米,试求 AB 的距离.
图 9
图 10 是古人测量古塔高度的示意图,测量人员的眼睛 A、标杆顶端 F 与古塔顶端 E 在同一直线上,已知此人的眼睛距地面 1.6 米,标杆高为 3 米,且 BC=2
米,CD=12 米,求古塔的高 ED.
图 10
如图 11,某公园景观河岸边有一灯杆 AB 高为 h,在灯光下,小林在点 D 处测得自己的影长 DF=3m,沿 BD 方向前进到达点 F 处测得自己的影长 FG=4m.设小林的身高为 1.8m.试求灯杆 AB 的高度 h 与求景观河 BD 的宽度 a.
图 11
能力挑战
(满分:25 分)
1.(5 分)在阳光下,小王和同学准备测量树的高度.却发现此时树的影子已不全落在地面上,有一部分落在教学楼的第一级台阶上(如图 1 所示),测得:大树落在地面上的影长为
4.5 米、落在第一级台阶上影子长为 0.2 米,并测得该一级台阶高为 0.3 米;同一时刻,另一名同学测得一根长为 l 米的竹竿的影长为 0.5 米,则树高为( ).
A.10 米 B.9.7 米 C.9.5 米 D.9.4 米
图 1 图 2
2.(5 分)如图 2,工地上竖立着两根电线杆 AB,CD,它们相距 5m,分别自两杆上高出地面 4m,6m 的 A,C 处,向两侧地面上的 E 和 D,B 和 F 处用钢丝绳拉紧,以固定电线杆, 那么钢丝绳 AD 与 BC 的交点 P 离地面的高度是 米.
3.(15 分)某兴趣小组开展课外活动.如图 3,A,B 两地相距 12 米,小明从点 A 出发沿 AB 方向匀速前进,2 秒后到达点 D,此时他(CD)在某一灯光下的影长为 AD,继续按原速行走 2 秒到达点 F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为 1.2 米,
然后他将速度提高到原来的 1.5 倍,再行走 2 秒到达点 H,此时他(GH)在同一灯光下的影长为 BH(点 C,E,G 在一条直线上).
请在图 3 中画出光源 O 点的位置,并画出他位于点 F 时在这个灯光下的影长 FM(不写画法).
求小明原来的速度.
图 3
参考答案基础闯关
1.D;2.A;3.C;4.A;5.B;
6.3.2; 7.12 米; 8.10 米; 9.9m; 10.2:5;
11. 300; 12.丙; 13.15 或 20;
透气窗口 AB 的高为 0.9m.
AB 两点的距离为 96 米.
古塔 ED 的高为 11.4 米.
AB ? FB
AB ? GB
由△ABF∽△CDF 可得 CD FD ,由△ABG∽△EFG 可得 EF GF ,又 CD=EF,故
GB ? FB
有 GF FD ,即
a ? 7 ? a ? 3 4 3
h ? 12
,解得 a=9;又由 FB=BD+FD=12,即有1.8 3
能力挑战
,解得 h=7.2.
1.B; 2.2.4.
3.(1)如图(利用中心投影知识作图).
( 2 ) 设 小 明 的 速 度 为 xm/s , 则 CE=AD=DF=2x , EG=3x , AM=AF-MF=4x-1.2 ,
AM ? OM
MB=AB-AM=13.2-4x.由△OAM ∽△ OCM 可得
MB ? OM
CE OE
AM ? MB
, 由△
OMB ∽ △ OEG 可 得
4x ?1.2 ? 13.2 ? 4x
EG OE
, 故 有
CE EG , 即
2x 3x
,解得 x=1.5,经检验 x=1.5 是原方程的解.即小
明的速度为 1.5m/s.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
