人教版九年级数学 下册 27.3 位似 课件(共41张PPT)
文档属性
| 名称 | 人教版九年级数学 下册 27.3 位似 课件(共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 919.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览







文档简介
(共41张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
1、我们学过的图形变换形式有哪些?
2、什么叫相似?相似与全等有什么区别与联系?
平移、旋转、对称
相似:形状相同。
全等:大小、形状相同,能够重合
区别:相似不一定全等,但全等一定相似。
联系:形状相同
知识回顾
相似图形
这种相似有什么特征?
提出问题
相似图形
这种相似有什么特征?
提出问题
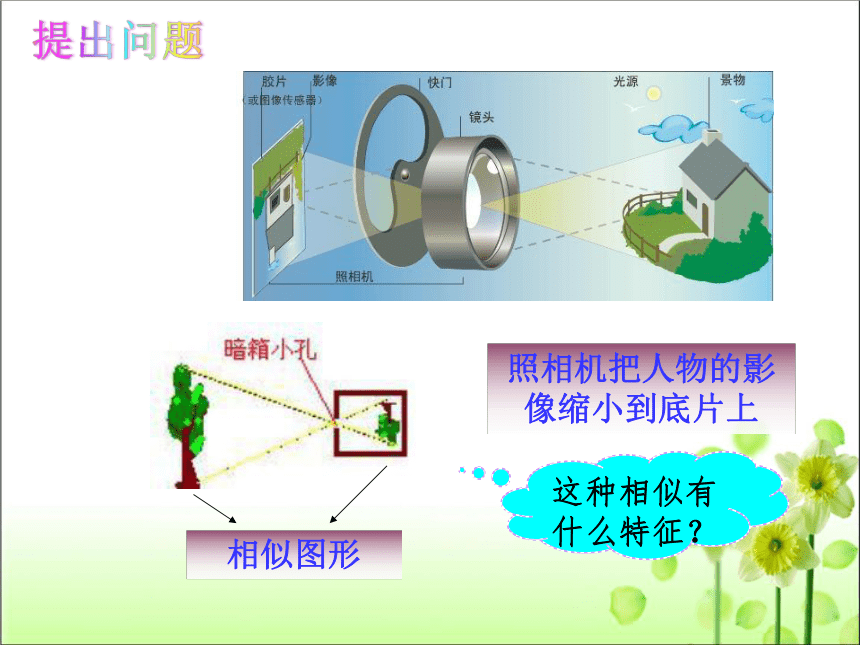
照相机把人物的影像缩小到底片上
相似图形
这种相似有什么特征?
提出问题
在幻灯机放映图片的过程中,这些图片有
什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
提出问题
27.3 位 似
人教版八年级数学 下册
目标导航
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质。
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小。
认真阅读课本中27.3 位似的内容,完成下面练习并体验知识点的形成过程。
自主研学
问题1: 在日常生活中,我们经常见到这样一类相似的图形,它们有什么特征?
在日常生活中,经常遇到一些把图形放大或缩小,但不改变图形的形状的情形。经过放大或缩小的图形,与原图形是相似的.用这样的方法,我们可以得到真实的图片和满意的照片.
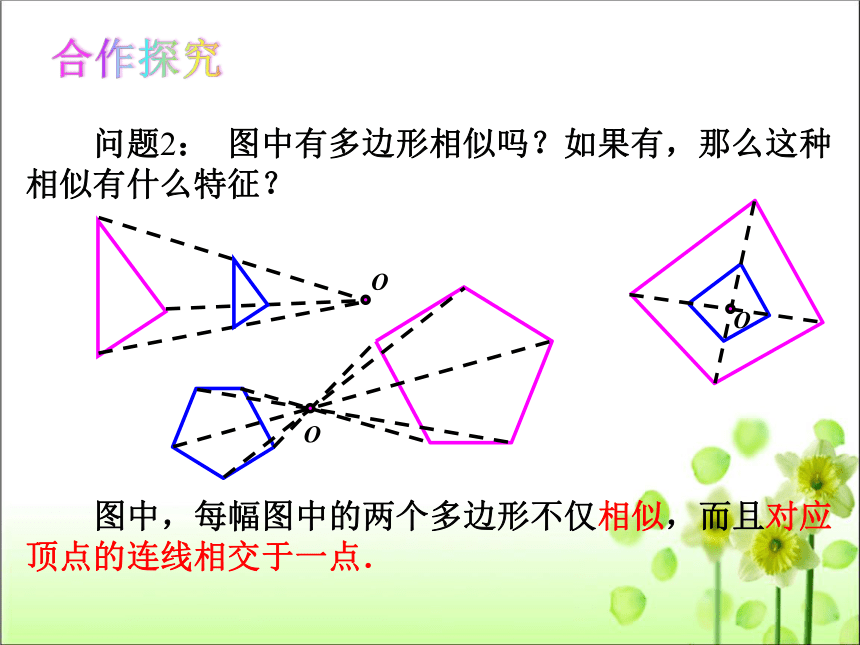
合作探究
问题2: 图中有多边形相似吗?如果有,那么这种相似有什么特征?
图中,每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点.
O
O
O
合作探究
位似图形的概念:
如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时的相似比又叫位似比.
明确
相似
对应顶点的连线相交于一点
合作探究
位似的特征:
1.位似图形一定是相似形,反之相似形不一定是位似图形.
2.判断位似图形时,要注意首先它们必须是相似形,其次每一对对应点所在直线都经过同一点.
合作探究
位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
注意
合作探究
位似的作用
位似可以将一个图形放大或缩小。
合作探究
1:判断下列各对图形哪些是位似图形,哪些不是.
(1)五边形ABCDE与五边形A′B′C′D′E′;
(2)在平行四边形ABCD中,△ABO与△CDO
是
不是
是
即学即练
判断下列各对图形哪些是位似图形,哪些不是.
(3)正方形ABCD与正方形A′B′C′D′.
(4)等边三角形ABC与等边三角形A′B′C′
是
是
即学即练
判断下列各对图形哪些是位似图形,哪些不是.
(6)扇形ABC与扇形A′B′C′,
(B、A 、B′在一条直线上,C、A 、C′在一条直线上)
是
是
即学即练
利用位似,可以将一个图形放大或缩小.
例如,要把四边形 ABCD 缩小到原来的 .
合作探究
C
D
B
A
●
●
●
●
●
A`
B`
C`
D`
O
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′、B′、C′、D′,使得
;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′,如图2.
作 法 一
问:此作图题还
有其它作法吗?
合作探究
如 图3
作 法 二
D
C
B
A
O
●
●
A`
B`
C`
D`
●
●
●
合作探究
如 图4.
总结:利用位似进行作图的关键是确定 __________和_________.
D
C
B
A
作 法 三
O
A`
B`
C`
D`
●
●
●
●
●
位似中心
关键点
合作探究
①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。
位似变换的步骤
归纳总结
如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
A
B
A'
B'
A〞
B〞
位似变换后A,B的对应点为A ' ( , ),B'( , );A"( , ),B" ( , ).
2
1
2
0
- 2
- 1
- 2
0
合作探究
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?
A
B
C
位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
12
4
-4
-6
-4
-2
-4
-12
A'
B'
C'
A"
B"
C"
合作探究
在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.
归纳总结
1. 位似图形、位似中心、位似比:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形。
这个点叫做位似中心。
这时的相似比又称为位似比.
课堂小结
2. 位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比。
以坐标原点为位似中心的位似变换有以下性质:若原图形上点的坐标为(x,y),与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky)。
课堂小结
画出基本图形。
选取位似中心。
根据条件确定对应点,并描出对应点。
顺次连结各对应点,所成的图形就是所求的图形。
3. 位似图形的画法:
1. 判断下列各对图形哪些是位似图形,哪些不是.
(1)五边形ABCDE与五边形A′B′C′D′E′
(2)正方形ABCD与正方A′B′C′D′
√
×
检测目标
(3)等边三角形ABC与等边三角形A′B′C′
√
检测目标
2、画出所给图中的位似中心.
●
●
●
(红点表示位似中心)
检测目标
3、画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A`B`C`D`E`。
E
D
C
O
●
B
A
●
●
●
●
●
A`
B`
D`
C`
E`
检测目标
(1)位似中心在△ABC的一条边AB上
B
A
C
B
A
B
A
B
A
B
A
(2)以点C为位似中心
B
A
C
B
A
B
A
B
A
B
A
假设位似中心点O在AB上,
相似比1:5,
点O位置如图(1)所示
o
●
●
A`
B`
C`
●
●
●
A`
B`
(C`)
●
●
检测目标
4、如图,△ABO 的三个顶点的坐标分别为
A(-2,4),B(-2,0), O(0,0).以原点 O 为
位似中心,画出一个三角形,使它与△ABO 的相似比
为 .
y
x
O
4
4
-4
-4
B
A
检测目标
5、如图,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?
O
A
B
C
D
AB∥CD
∵△OAB与△ODC是位似图形
∴△OAB∽△OCD
∴∠A∽∠C
AB∥CD
检测目标
例 如图,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为 的位似图形.
分析:问题的关键是要确定位似图形各个顶点的坐标.根据前面的规律,点A的对应点A‘的坐标为 ,即(-3,3).类似地,可以确定其他顶点的坐标.
解:如图,利用位似变换中对应点的坐标的变化规律.分别取点
A'( , ),B ' ( , ),
C ' ( , ),D'( , ).
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
A
B
C
D
A'
B'
C'
D'
- 3
3
- 4
1
-2
0
-1
2
依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形.
就这一个结果吗?
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
1、我们学过的图形变换形式有哪些?
2、什么叫相似?相似与全等有什么区别与联系?
平移、旋转、对称
相似:形状相同。
全等:大小、形状相同,能够重合
区别:相似不一定全等,但全等一定相似。
联系:形状相同
知识回顾
相似图形
这种相似有什么特征?
提出问题
相似图形
这种相似有什么特征?
提出问题
照相机把人物的影像缩小到底片上
相似图形
这种相似有什么特征?
提出问题
在幻灯机放映图片的过程中,这些图片有
什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
提出问题
27.3 位 似
人教版八年级数学 下册
目标导航
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质。
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小。
认真阅读课本中27.3 位似的内容,完成下面练习并体验知识点的形成过程。
自主研学
问题1: 在日常生活中,我们经常见到这样一类相似的图形,它们有什么特征?
在日常生活中,经常遇到一些把图形放大或缩小,但不改变图形的形状的情形。经过放大或缩小的图形,与原图形是相似的.用这样的方法,我们可以得到真实的图片和满意的照片.
合作探究
问题2: 图中有多边形相似吗?如果有,那么这种相似有什么特征?
图中,每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点.
O
O
O
合作探究
位似图形的概念:
如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时的相似比又叫位似比.
明确
相似
对应顶点的连线相交于一点
合作探究
位似的特征:
1.位似图形一定是相似形,反之相似形不一定是位似图形.
2.判断位似图形时,要注意首先它们必须是相似形,其次每一对对应点所在直线都经过同一点.
合作探究
位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
注意
合作探究
位似的作用
位似可以将一个图形放大或缩小。
合作探究
1:判断下列各对图形哪些是位似图形,哪些不是.
(1)五边形ABCDE与五边形A′B′C′D′E′;
(2)在平行四边形ABCD中,△ABO与△CDO
是
不是
是
即学即练
判断下列各对图形哪些是位似图形,哪些不是.
(3)正方形ABCD与正方形A′B′C′D′.
(4)等边三角形ABC与等边三角形A′B′C′
是
是
即学即练
判断下列各对图形哪些是位似图形,哪些不是.
(6)扇形ABC与扇形A′B′C′,
(B、A 、B′在一条直线上,C、A 、C′在一条直线上)
是
是
即学即练
利用位似,可以将一个图形放大或缩小.
例如,要把四边形 ABCD 缩小到原来的 .
合作探究
C
D
B
A
●
●
●
●
●
A`
B`
C`
D`
O
(1)在四边形ABCD外任取一点O;
(2)过点O分别作射线OA,OB,OC,OD;
(3)分别在射线OA,OB,OC,OD上取点A′、B′、C′、D′,使得
;
(4)顺次连接A′B′、B′C′、C′D′、D′A′,得到所要画的四边形A′B′C′D′,如图2.
作 法 一
问:此作图题还
有其它作法吗?
合作探究
如 图3
作 法 二
D
C
B
A
O
●
●
A`
B`
C`
D`
●
●
●
合作探究
如 图4.
总结:利用位似进行作图的关键是确定 __________和_________.
D
C
B
A
作 法 三
O
A`
B`
C`
D`
●
●
●
●
●
位似中心
关键点
合作探究
①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。
位似变换的步骤
归纳总结
如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
A
B
A'
B'
A〞
B〞
位似变换后A,B的对应点为A ' ( , ),B'( , );A"( , ),B" ( , ).
2
1
2
0
- 2
- 1
- 2
0
合作探究
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?
A
B
C
位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
12
4
-4
-6
-4
-2
-4
-12
A'
B'
C'
A"
B"
C"
合作探究
在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.
归纳总结
1. 位似图形、位似中心、位似比:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形。
这个点叫做位似中心。
这时的相似比又称为位似比.
课堂小结
2. 位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比。
以坐标原点为位似中心的位似变换有以下性质:若原图形上点的坐标为(x,y),与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky)。
课堂小结
画出基本图形。
选取位似中心。
根据条件确定对应点,并描出对应点。
顺次连结各对应点,所成的图形就是所求的图形。
3. 位似图形的画法:
1. 判断下列各对图形哪些是位似图形,哪些不是.
(1)五边形ABCDE与五边形A′B′C′D′E′
(2)正方形ABCD与正方A′B′C′D′
√
×
检测目标
(3)等边三角形ABC与等边三角形A′B′C′
√
检测目标
2、画出所给图中的位似中心.
●
●
●
(红点表示位似中心)
检测目标
3、画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A`B`C`D`E`。
E
D
C
O
●
B
A
●
●
●
●
●
A`
B`
D`
C`
E`
检测目标
(1)位似中心在△ABC的一条边AB上
B
A
C
B
A
B
A
B
A
B
A
(2)以点C为位似中心
B
A
C
B
A
B
A
B
A
B
A
假设位似中心点O在AB上,
相似比1:5,
点O位置如图(1)所示
o
●
●
A`
B`
C`
●
●
●
A`
B`
(C`)
●
●
检测目标
4、如图,△ABO 的三个顶点的坐标分别为
A(-2,4),B(-2,0), O(0,0).以原点 O 为
位似中心,画出一个三角形,使它与△ABO 的相似比
为 .
y
x
O
4
4
-4
-4
B
A
检测目标
5、如图,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?
O
A
B
C
D
AB∥CD
∵△OAB与△ODC是位似图形
∴△OAB∽△OCD
∴∠A∽∠C
AB∥CD
检测目标
例 如图,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为 的位似图形.
分析:问题的关键是要确定位似图形各个顶点的坐标.根据前面的规律,点A的对应点A‘的坐标为 ,即(-3,3).类似地,可以确定其他顶点的坐标.
解:如图,利用位似变换中对应点的坐标的变化规律.分别取点
A'( , ),B ' ( , ),
C ' ( , ),D'( , ).
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
A
B
C
D
A'
B'
C'
D'
- 3
3
- 4
1
-2
0
-1
2
依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形.
就这一个结果吗?
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
