6.1.1 平方根课件
图片预览










文档简介
(共30张PPT)
人教版 七年级数学下
6.1 平方根(第一课时)
学习目标
1.了解算术平方根的概念,求非负数的算术平方根;(重点)
2.了解算术平方根的性质;(重点)
3.会估算一个数的算术平方根的大致范围,掌握估算方法,形成估算的意识,(难点)
4.会用计算器求一个数的算术平方根。
情境导入
你是怎么算出来的?
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
解:
∵52=25
∴正方形画框的边长为5dm.
5dm
25 dm2
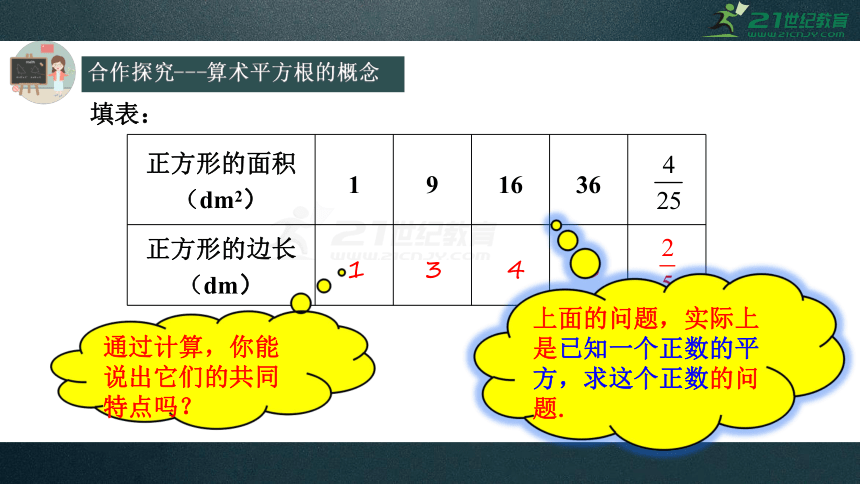
合作探究---算术平方根的概念
填表:
正方形的面积
(dm2) 1 9 16 36
正方形的边长
(dm)
1
3
4
6
通过计算,你能说出它们的共同特点吗?
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
定义:一般地,如果一个正数x的平方等于a ,即x2=a ,那么这个正数x叫做a的算术平方根.
a的算术平方根记为 ,
读作: “根号a ”,
a叫做被开方数.
5dm
25 dm2
a
x
x2=a
规定:0的算术平方根是0
合作探究---算术平方根的概念
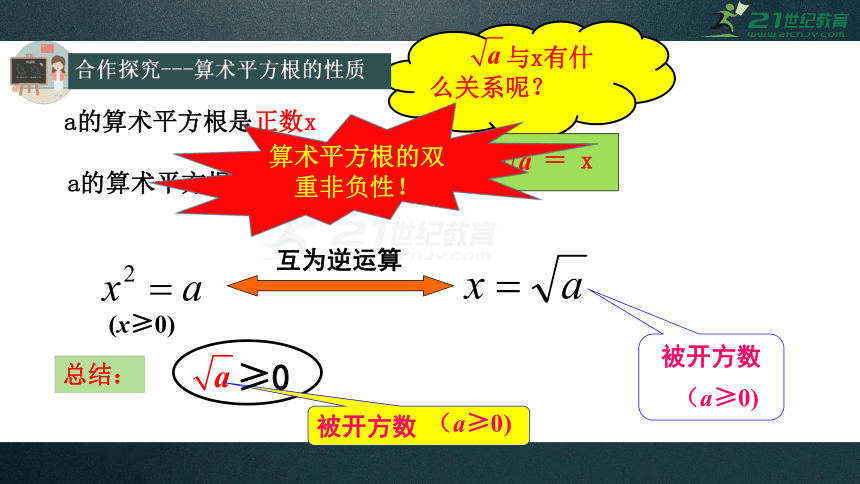
与x有什么关系呢?
a的算术平方根记为 ,
a的算术平方根是正数x
= x
合作探究---算术平方根的性质
互为逆运算
被开方数
(a≥0)
(x≥0)
算术平方根的双重非负性!
总结:
被开方数
(a≥0)
≥0
典例精析
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(1)因为102=100,
所以100的算术平方根是10.
即 .
典例精析
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(2)因为 ,
所以 的算术平方根是 .
即 .
典例精析
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(3)因为0.012=0.000 1,
所以0.000 1的算术平方根是0.01.
即 .
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
被开数越大,
对应的算术平方根也越大
被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
合作探究---算术平方根的性质
合作探究---算术平方根的性质
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2. 0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有1个
合作与交流:
小试牛刀
1、下列各式有意义吗?为什么.
解:(1) 无意义,负数没有算术平方根;
(2) 有意义,表示5的算术平方根的相反数;
(3) 有意义,表示 (-5)2 的算术平方根.
25
小试牛刀
解: 因为|m-1| ≥0, ≥0,又|m-1| + =0,
所以 |m-1| =0, =0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
2、若|m-1| + =0,求m+n的值.
几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
归纳
合作探究---估算范围
思考1:能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
拼成的这个大正方形的面积是2dm2,它的边长是多少呢?
解: 设大正方形的边长为x dm,
则 x2=2,
由算术平方根的定义可知, .
∴大正方形的边长为 dm.
∵12=1, 22=4
∴1< <2
思考2: 有多大呢?
∵1.42=1.96, 1.52=2.25
∴1.4< <1.5
想一想: 介于哪两个连续整数之间?
答: 介于1与2这两个整数之间.
合作探究---估算范围
∵1.412=1.9881,
1.422=2.0164
∴1.41< <1.42
∵1.4142=1.999396, 1.452=2.002225
∴1.414< <1.415
……
是无限不循环小数,你以前见过这种数吗?
小试牛刀
1.说一说 介于哪两个连续整数之间?
解: 介于2与3这两个整数之间.
介于3与4这两个整数之间.
介于6与7这两个整数之间.
2.比较大小:
(1)3 _____ (2)12 _____
(3) _____0.5
<
>
>
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数a的算术平方根(或其近似数).
a
=
按键顺序:
合作探究---正确使用计算器
合作探究---正确使用计算器
1、用计算器求下列各式的值:
(1) ;(2) (精确到0.001).
解:(1) 依次按键 、3136、 ,
显示:56.
∴ .
(2) 依次按键 、2、 ,
显示:1.414213562.
∴ .
2、利用计算器计算,并将计算结果填在表中,你发现了什么规律?
… …
… …
0.25
2.5
25
250
0.791
7.91
79.1
规律:被开方数的小数点向右(或向左)移动2位,其算术平方根的小数点向右(或向左)移动1位.
合作探究---正确使用计算器
小试牛刀
3.你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
想一想: 你能否根据 的值说出 是多少?
解:
答:不能
能力提升
4、小丽想用一块面积为400 cm2为的长方形纸片,沿着边的方向剪出一块面积为300 cm2的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁,小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”
你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
能力提升
解:设剪出的长方形的两边长分别为3x cm和2x cm,
则有:3x ? 2x=300
6x2=300
x2=50
故长方形纸片的长为 ,宽为 .
小丽能用这块纸片裁出符合要求的纸片吗?
能力提升
∵50>49,
∴ >3×7=21,
∵原正方形的边长为: ,而21 >20
∴ >20,
∴不同意小明的说法,小丽不能用这块纸片裁出符合要求的纸片.
课堂总结
今天我们学习了哪些知识?
1.什么是算术平方根?
2. 算术平方根的性质是有哪些?
3.如何估算算术平方根的大小?
4.如何操作计算器计算一个数的算数平方根?
综合演练
1、下列说法正确的是( )
A、因为 ,所以3是9的算数平方根
B、因为 ,所以-3是9的算数平方根
C、因为 ,所以-3和3是9的算数平方根
D、以上说法都不对
A
知识点拨:根据算数平方根的定义可知只有A对。
综合演练
2、设a是一个数的算术平方根,那么( )
A、a≥0 B、a>0 C、a<0 D、a≤0
A
知识点拨:根据算数平方根的双重非负性可知只有A对。
3、下列算式有意义的是( )
A、 B、 C、 D、
C
知识点拨:根据算数平方根的双重非负性可知只有C对。
综合演练
4.估计 的大小在( )
A. 5~6之间 B. 6~7之间
C. 7~8之间 D. 8~9之间
C
知识点拨:因为 ,所以在7到
8之前,选C。
2
5. 的算术平方根是______;
6.一个数的算术平方根是它本身,则这个数是______;
1和0
综合演练
7.已知: (x-2)2+| y-3 | + =0,
求2x-3y +z的值?
解:∵ (x-2)2+| y-3 | + =0
∴ (x-2)2=0,| y-3 | =0,
∴ x=2,y=3,z=4
∴ 2x-3y + z=4-9 +4=-1
课后作业
课本教材第47页:1、2、5、7题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级数学下
6.1 平方根(第一课时)
学习目标
1.了解算术平方根的概念,求非负数的算术平方根;(重点)
2.了解算术平方根的性质;(重点)
3.会估算一个数的算术平方根的大致范围,掌握估算方法,形成估算的意识,(难点)
4.会用计算器求一个数的算术平方根。
情境导入
你是怎么算出来的?
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
解:
∵52=25
∴正方形画框的边长为5dm.
5dm
25 dm2
合作探究---算术平方根的概念
填表:
正方形的面积
(dm2) 1 9 16 36
正方形的边长
(dm)
1
3
4
6
通过计算,你能说出它们的共同特点吗?
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
定义:一般地,如果一个正数x的平方等于a ,即x2=a ,那么这个正数x叫做a的算术平方根.
a的算术平方根记为 ,
读作: “根号a ”,
a叫做被开方数.
5dm
25 dm2
a
x
x2=a
规定:0的算术平方根是0
合作探究---算术平方根的概念
与x有什么关系呢?
a的算术平方根记为 ,
a的算术平方根是正数x
= x
合作探究---算术平方根的性质
互为逆运算
被开方数
(a≥0)
(x≥0)
算术平方根的双重非负性!
总结:
被开方数
(a≥0)
≥0
典例精析
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(1)因为102=100,
所以100的算术平方根是10.
即 .
典例精析
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(2)因为 ,
所以 的算术平方根是 .
即 .
典例精析
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(3)因为0.012=0.000 1,
所以0.000 1的算术平方根是0.01.
即 .
例1:求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
被开数越大,
对应的算术平方根也越大
被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
合作探究---算术平方根的性质
合作探究---算术平方根的性质
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2. 0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有1个
合作与交流:
小试牛刀
1、下列各式有意义吗?为什么.
解:(1) 无意义,负数没有算术平方根;
(2) 有意义,表示5的算术平方根的相反数;
(3) 有意义,表示 (-5)2 的算术平方根.
25
小试牛刀
解: 因为|m-1| ≥0, ≥0,又|m-1| + =0,
所以 |m-1| =0, =0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
2、若|m-1| + =0,求m+n的值.
几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
归纳
合作探究---估算范围
思考1:能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
拼成的这个大正方形的面积是2dm2,它的边长是多少呢?
解: 设大正方形的边长为x dm,
则 x2=2,
由算术平方根的定义可知, .
∴大正方形的边长为 dm.
∵12=1, 22=4
∴1< <2
思考2: 有多大呢?
∵1.42=1.96, 1.52=2.25
∴1.4< <1.5
想一想: 介于哪两个连续整数之间?
答: 介于1与2这两个整数之间.
合作探究---估算范围
∵1.412=1.9881,
1.422=2.0164
∴1.41< <1.42
∵1.4142=1.999396, 1.452=2.002225
∴1.414< <1.415
……
是无限不循环小数,你以前见过这种数吗?
小试牛刀
1.说一说 介于哪两个连续整数之间?
解: 介于2与3这两个整数之间.
介于3与4这两个整数之间.
介于6与7这两个整数之间.
2.比较大小:
(1)3 _____ (2)12 _____
(3) _____0.5
<
>
>
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数a的算术平方根(或其近似数).
a
=
按键顺序:
合作探究---正确使用计算器
合作探究---正确使用计算器
1、用计算器求下列各式的值:
(1) ;(2) (精确到0.001).
解:(1) 依次按键 、3136、 ,
显示:56.
∴ .
(2) 依次按键 、2、 ,
显示:1.414213562.
∴ .
2、利用计算器计算,并将计算结果填在表中,你发现了什么规律?
… …
… …
0.25
2.5
25
250
0.791
7.91
79.1
规律:被开方数的小数点向右(或向左)移动2位,其算术平方根的小数点向右(或向左)移动1位.
合作探究---正确使用计算器
小试牛刀
3.你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
想一想: 你能否根据 的值说出 是多少?
解:
答:不能
能力提升
4、小丽想用一块面积为400 cm2为的长方形纸片,沿着边的方向剪出一块面积为300 cm2的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁,小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”
你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
能力提升
解:设剪出的长方形的两边长分别为3x cm和2x cm,
则有:3x ? 2x=300
6x2=300
x2=50
故长方形纸片的长为 ,宽为 .
小丽能用这块纸片裁出符合要求的纸片吗?
能力提升
∵50>49,
∴ >3×7=21,
∵原正方形的边长为: ,而21 >20
∴ >20,
∴不同意小明的说法,小丽不能用这块纸片裁出符合要求的纸片.
课堂总结
今天我们学习了哪些知识?
1.什么是算术平方根?
2. 算术平方根的性质是有哪些?
3.如何估算算术平方根的大小?
4.如何操作计算器计算一个数的算数平方根?
综合演练
1、下列说法正确的是( )
A、因为 ,所以3是9的算数平方根
B、因为 ,所以-3是9的算数平方根
C、因为 ,所以-3和3是9的算数平方根
D、以上说法都不对
A
知识点拨:根据算数平方根的定义可知只有A对。
综合演练
2、设a是一个数的算术平方根,那么( )
A、a≥0 B、a>0 C、a<0 D、a≤0
A
知识点拨:根据算数平方根的双重非负性可知只有A对。
3、下列算式有意义的是( )
A、 B、 C、 D、
C
知识点拨:根据算数平方根的双重非负性可知只有C对。
综合演练
4.估计 的大小在( )
A. 5~6之间 B. 6~7之间
C. 7~8之间 D. 8~9之间
C
知识点拨:因为 ,所以在7到
8之前,选C。
2
5. 的算术平方根是______;
6.一个数的算术平方根是它本身,则这个数是______;
1和0
综合演练
7.已知: (x-2)2+| y-3 | + =0,
求2x-3y +z的值?
解:∵ (x-2)2+| y-3 | + =0
∴ (x-2)2=0,| y-3 | =0,
∴ x=2,y=3,z=4
∴ 2x-3y + z=4-9 +4=-1
课后作业
课本教材第47页:1、2、5、7题
https://www.21cnjy.com/help/help_extract.php
