人教版七年级下数学第5章平行线的性质与判定书写专题练习卷(无答案)
文档属性
| 名称 | 人教版七年级下数学第5章平行线的性质与判定书写专题练习卷(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 19:31:37 | ||
图片预览

文档简介
七年级数学平行线专题测试卷
1.如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数(填理由或数学式)
解:∵∠3=131° ( )
又∵∠3=∠1 ( )
∴∠1= ( )
∵a∥b ( )
∴∠1+∠2=180° ( )
∴∠2= ( ).
2.如图,EF∥AD,∠1=∠2∠BAC=80°.求∠AGD=?
因为EF∥AD,
所以∠2= ( ),
又因为∠1=∠2,
所以∠1=∠3( ),
所以AB∥ ( ),
所以∠BAC+ =180°( ),
因为∠BAC=80°,所以∠AGD= .
3.推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.
证明:∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换)
∴AB∥CD ( )
4.如图已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°.
请完善说明过程,并在括号内填上相应依据
解:∵AD∥BC
∴∠1=∠3 ( ),
∵∠1=∠2(已知)
∴∠2=∠3( ),
∴ ∥ ( ),
∴∠3+∠4=180°( )
5.按图填空,并注明理由.
已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
证明:∵∠1=∠2 (已知)
∴ ∥ ( )
∴∠E=∠ ( )
又∵∠E=∠3 ( 已知 )
∴∠3=∠
( )
∴AD∥BE.
( )
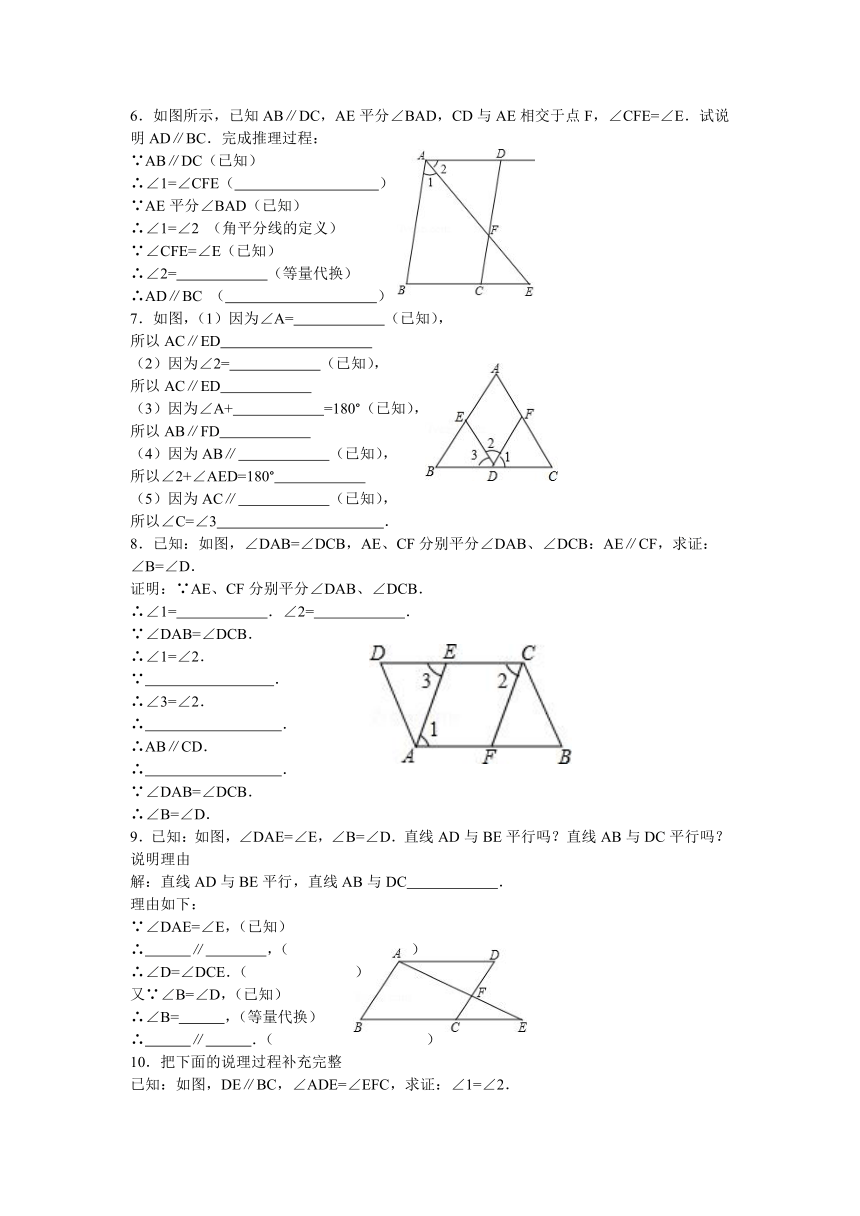
6.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE( )
∵AE平分∠BAD(已知)
∴∠1=∠2 (角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2= (等量代换)
∴AD∥BC ( )
7.如图,(1)因为∠A= (已知),
所以AC∥ED
(2)因为∠2= (已知),
所以AC∥ED
(3)因为∠A+ =180°(已知),
所以AB∥FD
(4)因为AB∥ (已知),
所以∠2+∠AED=180°
(5)因为AC∥ (已知),
所以∠C=∠3 .
8.已知:如图,∠DAB=∠DCB,AE、CF分别平分∠DAB、∠DCB:AE∥CF,求证:∠B=∠D.
证明:∵AE、CF分别平分∠DAB、∠DCB.
∴∠1= .∠2= .
∵∠DAB=∠DCB.
∴∠1=∠2.
∵ .
∴∠3=∠2.
∴ .
∴AB∥CD.
∴ .
∵∠DAB=∠DCB.
∴∠B=∠D.
9.已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由
解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,( )
∴∠D=∠DCE.( )
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .( )
10.把下面的说理过程补充完整
已知:如图,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
证明:∵DE∥BC(已知)
∴∠ADE= ( )
∵∠ADE=∠EFC(已知)
∴ = ( )
∴DB∥EF( )
∴∠1=∠2( )
11.如图,已知DE∥AC,∠A=∠DEF,试说明∠B=∠FEC.
解:∵DE∥AC(已知)
∴∠A=∠BDE( )
∵∠A=∠DEF( )
∴∠ =∠
∴AB∥EF( )
∴∠B=∠FEC( )
12.已知:如图,AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD.
∵EG平分∠AEF,FH平分∠EFD.( )
∴∠ =∠AEF,
∠ =∠EFD,(角平分线定义)
∴∠ =∠ ,
∴EG∥FH. .
13.如图所示,根据题意填空已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.
证明:∵AB∥CD,(已知)
∴∠BAC+∠ACD=180°,
( )
又∵AE平分∠BAC,CE平分∠ACD,
( )
∴∠1=∠BAC,∠2=∠ACD,
( )
∴∠1+∠2=(∠BAC+∠ACD)=×180°=90°.
即∠1+∠2=90°.
结论:若两条平行线被第三条直线所截,则一组同旁内角的平分线互相 .
推广:若两条平行线被第三条直线所截,则一组同位角的平分线互相 .内错角的角平分线互相 .
14.如图,已知AD⊥BC,EF⊥BC,∠1=∠2,∠BAC=80°,求∠AMD的度数.
解:∵AD⊥BC,EF⊥BC(已知),
∴AD∥ ,
( )
∴ =∠3
( ).
又∵∠1=∠2(已知),
∴∠2= ( ),
∴ ∥ ( ),
∴∠BAC+ =180°( ),
又∵∠BAC=80°,
∴∠AMD=180°﹣80°=100°.
15.如图,A、B、C三点在同一直线上,且∠1=∠2,∠3=∠D,求证:BD∥CE.
证明:∵∠1=∠2 ,
∴AD∥ ( ),
∴ =∠DBE( ),
又∵∠3=∠D(已知),
∴∠3=∠DBE( ),
∴BD∥CE( ).
16.已知:如图,点A、B、C在一条直线上,AD∥BE,∠1=∠2.
求证:∠A=∠E 的过程填空完整.
证明:∵AD∥BE( 已知 ),
∴∠A= ( ),
又∵∠1=∠2( 已知 ),
∴ED∥ ( ),
∴∠E= ( ),
∴∠A=∠E( ).
17.阅读第(1)题解题过程,解答第(2)题.
(1)如图1,AB∥CD,E为AB、CD之间的一点,已知∠B=40°,∠C=30°,求∠BEC的度数.
解:过点E作EM∥AB,
∴∠B= ( ).
∵AB∥CD,AB∥EM,
∴EM∥ ( ).
∴∠2= ( ).
∴∠BEC=∠1+∠2=∠B+∠C=40°+30°=70°.
(2)如图2,AB∥ED,试探究∠B、∠BCD、∠D之间的数量关系.
18.如图,已知CF⊥AB于F,DE⊥AB于E,FG∥BC,求证:∠1=∠2.
证明:∵CF⊥AB,DE⊥AB,(已知)
∴∠BDE=90°,∠BFC=90°,(垂直的定义)
∴∠BDE=∠BFC,(等量代换)
∴ ,(同位角相等,两直线平行)
∴∠1=∠BCF( )
∵FG∥BC,(已知)
∴ ,(两直线平行,内错角相等)
∴∠1=∠2.( )
19.如图,已知DE∥BC,DF、BE分别平分∠ADE和∠ABC,求证:∠FDE=∠DEB.
证明:∵DE∥BC
∴∠ADE= ( )
∵DF、BE平分∠ADE、∠ABC
∴∠ADF= ( )
∴∠ABE= ( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠ ( )
20.如图,已知E、F分别在AB、CD上,BC交AF于点G,交DE于点M,若∠1=∠2,∠A=∠D.
(1)AF与ED平行吗?请说明理由;
(2)试说明∠B=∠C;
解:(1)AF∥ED.理由如下:
∵∠1=∠2(已知)
∠1=∠CBD( )
∴ ∥ ( )
(2)∵AF∥ED(已知)
∴∠AFC=∠ ( )
又∵∠A=∠D(已知)
∴∠A=∠ ( )
1.如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数(填理由或数学式)
解:∵∠3=131° ( )
又∵∠3=∠1 ( )
∴∠1= ( )
∵a∥b ( )
∴∠1+∠2=180° ( )
∴∠2= ( ).
2.如图,EF∥AD,∠1=∠2∠BAC=80°.求∠AGD=?
因为EF∥AD,
所以∠2= ( ),
又因为∠1=∠2,
所以∠1=∠3( ),
所以AB∥ ( ),
所以∠BAC+ =180°( ),
因为∠BAC=80°,所以∠AGD= .
3.推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.
证明:∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换)
∴AB∥CD ( )
4.如图已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°.
请完善说明过程,并在括号内填上相应依据
解:∵AD∥BC
∴∠1=∠3 ( ),
∵∠1=∠2(已知)
∴∠2=∠3( ),
∴ ∥ ( ),
∴∠3+∠4=180°( )
5.按图填空,并注明理由.
已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
证明:∵∠1=∠2 (已知)
∴ ∥ ( )
∴∠E=∠ ( )
又∵∠E=∠3 ( 已知 )
∴∠3=∠
( )
∴AD∥BE.
( )
6.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE( )
∵AE平分∠BAD(已知)
∴∠1=∠2 (角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2= (等量代换)
∴AD∥BC ( )
7.如图,(1)因为∠A= (已知),
所以AC∥ED
(2)因为∠2= (已知),
所以AC∥ED
(3)因为∠A+ =180°(已知),
所以AB∥FD
(4)因为AB∥ (已知),
所以∠2+∠AED=180°
(5)因为AC∥ (已知),
所以∠C=∠3 .
8.已知:如图,∠DAB=∠DCB,AE、CF分别平分∠DAB、∠DCB:AE∥CF,求证:∠B=∠D.
证明:∵AE、CF分别平分∠DAB、∠DCB.
∴∠1= .∠2= .
∵∠DAB=∠DCB.
∴∠1=∠2.
∵ .
∴∠3=∠2.
∴ .
∴AB∥CD.
∴ .
∵∠DAB=∠DCB.
∴∠B=∠D.
9.已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由
解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,( )
∴∠D=∠DCE.( )
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .( )
10.把下面的说理过程补充完整
已知:如图,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
证明:∵DE∥BC(已知)
∴∠ADE= ( )
∵∠ADE=∠EFC(已知)
∴ = ( )
∴DB∥EF( )
∴∠1=∠2( )
11.如图,已知DE∥AC,∠A=∠DEF,试说明∠B=∠FEC.
解:∵DE∥AC(已知)
∴∠A=∠BDE( )
∵∠A=∠DEF( )
∴∠ =∠
∴AB∥EF( )
∴∠B=∠FEC( )
12.已知:如图,AB∥CD,EF分别交于AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD.
∵EG平分∠AEF,FH平分∠EFD.( )
∴∠ =∠AEF,
∠ =∠EFD,(角平分线定义)
∴∠ =∠ ,
∴EG∥FH. .
13.如图所示,根据题意填空已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.
证明:∵AB∥CD,(已知)
∴∠BAC+∠ACD=180°,
( )
又∵AE平分∠BAC,CE平分∠ACD,
( )
∴∠1=∠BAC,∠2=∠ACD,
( )
∴∠1+∠2=(∠BAC+∠ACD)=×180°=90°.
即∠1+∠2=90°.
结论:若两条平行线被第三条直线所截,则一组同旁内角的平分线互相 .
推广:若两条平行线被第三条直线所截,则一组同位角的平分线互相 .内错角的角平分线互相 .
14.如图,已知AD⊥BC,EF⊥BC,∠1=∠2,∠BAC=80°,求∠AMD的度数.
解:∵AD⊥BC,EF⊥BC(已知),
∴AD∥ ,
( )
∴ =∠3
( ).
又∵∠1=∠2(已知),
∴∠2= ( ),
∴ ∥ ( ),
∴∠BAC+ =180°( ),
又∵∠BAC=80°,
∴∠AMD=180°﹣80°=100°.
15.如图,A、B、C三点在同一直线上,且∠1=∠2,∠3=∠D,求证:BD∥CE.
证明:∵∠1=∠2 ,
∴AD∥ ( ),
∴ =∠DBE( ),
又∵∠3=∠D(已知),
∴∠3=∠DBE( ),
∴BD∥CE( ).
16.已知:如图,点A、B、C在一条直线上,AD∥BE,∠1=∠2.
求证:∠A=∠E 的过程填空完整.
证明:∵AD∥BE( 已知 ),
∴∠A= ( ),
又∵∠1=∠2( 已知 ),
∴ED∥ ( ),
∴∠E= ( ),
∴∠A=∠E( ).
17.阅读第(1)题解题过程,解答第(2)题.
(1)如图1,AB∥CD,E为AB、CD之间的一点,已知∠B=40°,∠C=30°,求∠BEC的度数.
解:过点E作EM∥AB,
∴∠B= ( ).
∵AB∥CD,AB∥EM,
∴EM∥ ( ).
∴∠2= ( ).
∴∠BEC=∠1+∠2=∠B+∠C=40°+30°=70°.
(2)如图2,AB∥ED,试探究∠B、∠BCD、∠D之间的数量关系.
18.如图,已知CF⊥AB于F,DE⊥AB于E,FG∥BC,求证:∠1=∠2.
证明:∵CF⊥AB,DE⊥AB,(已知)
∴∠BDE=90°,∠BFC=90°,(垂直的定义)
∴∠BDE=∠BFC,(等量代换)
∴ ,(同位角相等,两直线平行)
∴∠1=∠BCF( )
∵FG∥BC,(已知)
∴ ,(两直线平行,内错角相等)
∴∠1=∠2.( )
19.如图,已知DE∥BC,DF、BE分别平分∠ADE和∠ABC,求证:∠FDE=∠DEB.
证明:∵DE∥BC
∴∠ADE= ( )
∵DF、BE平分∠ADE、∠ABC
∴∠ADF= ( )
∴∠ABE= ( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠ ( )
20.如图,已知E、F分别在AB、CD上,BC交AF于点G,交DE于点M,若∠1=∠2,∠A=∠D.
(1)AF与ED平行吗?请说明理由;
(2)试说明∠B=∠C;
解:(1)AF∥ED.理由如下:
∵∠1=∠2(已知)
∠1=∠CBD( )
∴ ∥ ( )
(2)∵AF∥ED(已知)
∴∠AFC=∠ ( )
又∵∠A=∠D(已知)
∴∠A=∠ ( )
