六年级数学下册试题 一课一练5.3图形与几何-《立体图形》-西师大版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练5.3图形与几何-《立体图形》-西师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 170.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 17:01:15 | ||
图片预览


文档简介
5.3图形与几何-《立体图形》
1.填一填。
(1)晴朗的日子里,从太阳出来到中午,树的影长越来越( )。
(2)一个正方体从不同的角度观察,一次最多能看到( )个面。
(3)下面是一个立体图形的展开图(单位:cm)。
①这个展开图可以折成一个( )。
②这个立体图形的棱长和是( )cm。
(4)用一根48厘米长的铁丝做成一个正方体框架,这个正方体的棱长为( )厘米。
(5)一个圆柱和一个圆锥的体积和底面积分别相等,圆锥的高是12厘米,圆柱的高是( )厘米。
(6)一块长方形铁皮恰好能制成一根底面直径是8厘米,长2米的圆柱形排水管,这块铁皮的长是( )米,宽是( )米。
(7)把一根圆柱形木料截成3个小圆柱,圆柱的表面积增加了420cm2,这根木料的底面积是( )。
(8)下面是一个( )的侧面展开图,这个立体图形的表面积是( )平方厘米,体积是( )立方厘米。
(9)一个正方体水池的棱长为3米,这个水池的占地面积是( )平方米,能盛水( )升。
2.判一判
(1)一个长方体可以分成两个完全一样的正方体,这个长方体定有一组相对的面是正方形。( )
(2)一个圆柱的侧面展开图是一个正方形,这个圆柱的高是底面半径的2π倍。( )
(3)棱长为6cm的正方体的表面积和体积相等。( )
(4)侧面积相等的两个圆柱,它们的底面积也一定相等。( )
(5)从圆锥的顶点向底面作垂直切割,所得到的横截面是一个等腰三角形。( )
(6)从圆锥的顶点到底面上任意一点的连线叫做圆锥的高。( )
3.学校教学楼的后方有一个电视发射塔。
(1)淘气走到位置A时,他能看到电视发射塔吗?如果能,请你画出来。
(2)淘气继续向前走,能够看到的电视发射塔的部分会怎样?
(3)当淘气走到位置B时,他还能看到电视发射塔吗?为什么?
4.搭一搭,想一想。
(1)一个立体图形,从上面看到的形状是,从左面看到的形状是,从正面看到的形状和从上面看到的形状是一样的。这个立体图形是由几个小立方块搭成的?
(2)一个立体图形,从正面看到的形状是,从上面看到的形状是。搭这样的立体图形,最少需要几个小立方块?最多需要多少个小立方块?
5.建造一个长方体游泳池,长30米,宽15米,深1.6米。在池子的底面和四壁砌瓷砖,如果每平方米需要25块,共需要多少块瓷砖?
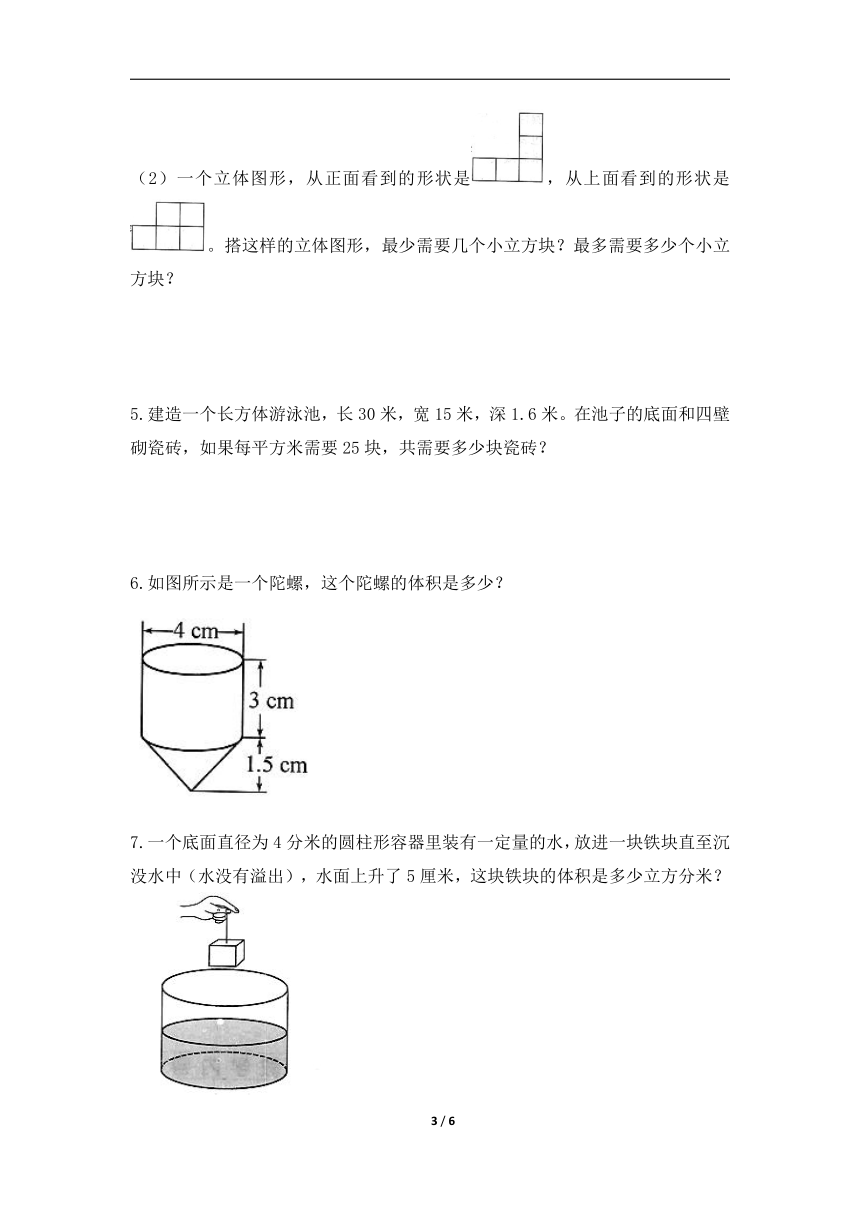
6.如图所示是一个陀螺,这个陀螺的体积是多少?
7.一个底面直径为4分米的圆柱形容器里装有一定量的水,放进一块铁块直至沉没水中(水没有溢出),水面上升了5厘米,这块铁块的体积是多少立方分米?
8.右图的“博士帽”是用卡纸做成的,上面是边长为30cm的正方形,下面是底面直径为16cm,高10cm的无底无盖的圆柱。制作这样的40顶“博士帽”,至少需要卡纸多少平方分米?
9.一个无盖的长方体玻璃鱼缸,长6分米,宽4分米,高3分米。
(1)做这样一个鱼缸大约需要多少平方分米玻璃?
(2)在鱼缸里注入40L水,水深大约多少厘米?
(3)往水里放人鹅卵石、水草和鱼,水面上升了2.5厘米,这些鹅卵石、水草和鱼的体积一共是多少立方分米?
10.“水立方”的游泳池是一个长方体,长50米,宽20米,水深1.。884米,池底装有底面直径为40cm的圆柱形排水管,排水时水的流速为50米/分,这样的5个排水管一起开,多少分放完这些水?
11.用一根铁丝可以做成一个长4厘米、宽3厘米、高2厘米的长方体框架,如果用它做成一个正方体框架,棱长是多少?
12.怎样移动下面立体图形中的小正方体,才能使从正面、上面看到的形状都是,从左面、右面看到的形状都是?
13.一个圆柱形水杯,底面半径是2.5cm,高是24cm,这个水杯的外包装盒是一个长方体,做这样一个包装盒至少要多少平方厘米硬纸板?
参考答案
1.(1)短 (2)3 (3)长方体 64 (4)4 (5)4 (6)2 0.2512
(7)105cm2 (8)圆柱 62.8 37.68 (9)9 27000
2.(1)√(2)√(3)×(4)×(5)√(6)×
3.(1)能(2)越来越少(3)不能,视线被教学楼挡住了。
4.(1)5个(2)7个9个
5.14850块
6.43.96cm3
7.6.28立方分米
8.560.96平方分米
9.(1)84平方分米 (2)厘米 (3)6立方分米
10.60分
11.3厘米
12.把左上方多的两块放在正面的上面一行,右侧多的这块也放在这一行
13.530平方厘米(提示:长方体包装盒的长、宽都等于圆柱的底面直径,高等于圆柱的高)
6 / 6
