苏科版七年级数学下册 第七章 平面图形的认识(二) 单元检测试卷(含答案)
文档属性
| 名称 | 苏科版七年级数学下册 第七章 平面图形的认识(二) 单元检测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 451.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览



文档简介
第 7 章 平面图形的认识(二) 单元检测
[时间:45 分钟 分值:100 分]
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分;在每个小题列出的四个选项中, 只有一项符合题意)
1.如图-1,与∠B 是同旁内角的角有( )
A.1 个 B.2 个 C.3 个 D.4 个
图-1
2.如图-2 所示,下列推理及括号中所注明的推理依据错误的是( )
图-2
A.因为∠1=∠3,所以 AB∥CD(内错角相等,两直线平行) B.因为 AB∥CD,所以∠1=∠3(两直线平行,内错角相等)
C.因为 AD∥BC,所以∠BAD+∠ABC=180°(两直线平行,同旁内角互补) D.因为∠DAM=∠CBM,所以 AB∥CD(两直线平行,同位角相等)
3.以下列长度的线段为边能构成三角形的是( ) A.1 cm,2 cm,3 cm B.2 cm,3 cm,4 cm C.4 cm,4 cm,9 cm D.1 cm,2 cm,4 cm
4.若一个多边形的每个内角均为 108°,则这个多边形是( ) A.七边形 B.六边形
C.五边形 D.四边形
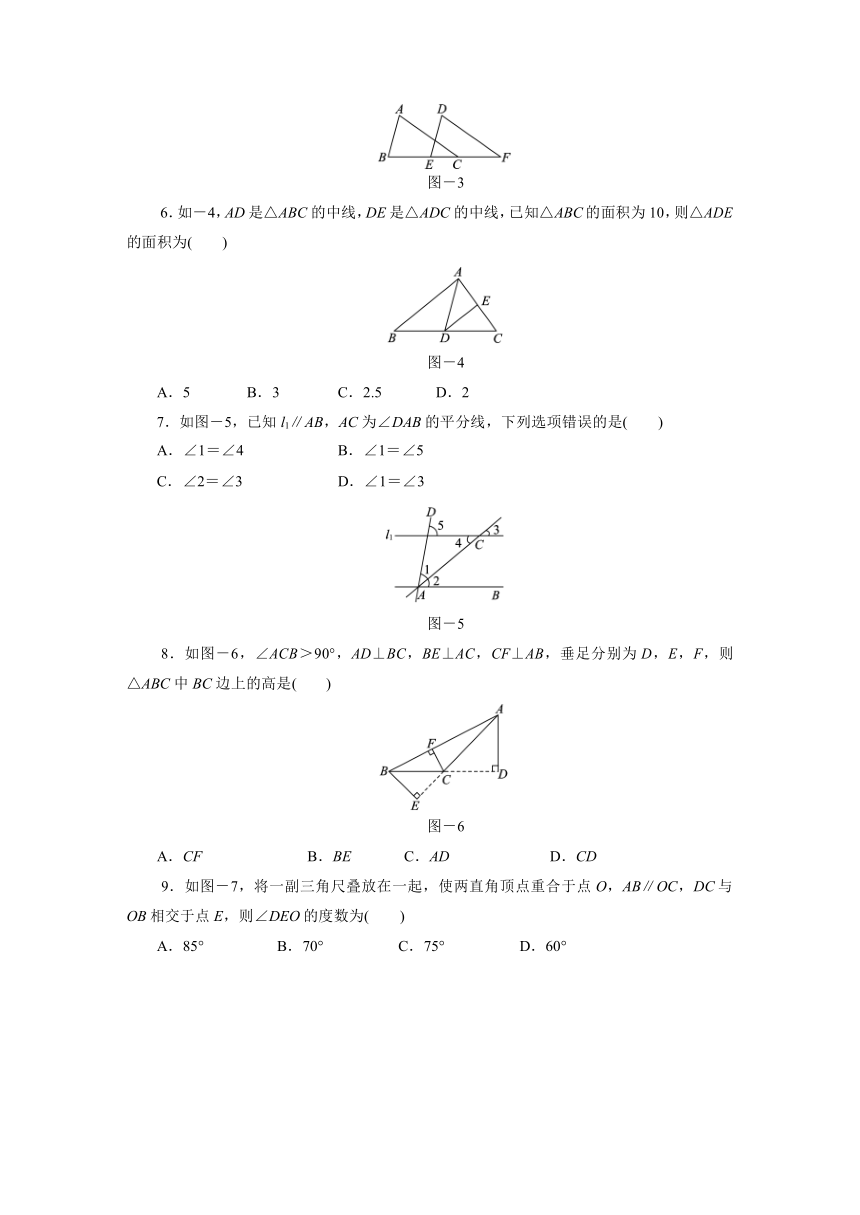
5.如图-3,在△ABC 中,BC=5,∠A=70°,∠B=75°,把△ABC 沿 BC 方向平移到
△DEF 的位置,若 CF=3,则下列结论错误的是( ) A.BE=3 B.∠F=35° C.DF=5 D.AB∥DE
图-3
6.如-4,AD 是△ABC 的中线,DE 是△ADC 的中线,已知△ABC 的面积为 10,则△ADE
的面积为( )
图-4
A.5 B.3 C.2.5 D.2
7.如图-5,已知 l1∥AB,AC 为∠DAB 的平分线,下列选项错误的是( ) A.∠1=∠4 B.∠1=∠5
C.∠2=∠3 D.∠1=∠3
图-5
8.如图-6,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为 D,E,F,则
△ABC 中 BC 边上的高是( )
图-6
A.CF B.BE C.AD D.CD
9.如图-7,将一副三角尺叠放在一起,使两直角顶点重合于点 O,AB∥OC,DC 与
OB 相交于点 E,则∠DEO 的度数为( )
A.85° B.70° C.75° D.60°
图-7
10.如图-8,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;
④∠AMC=∠BND.其中正确的是( )
图-8
A.①②④ B.②③④ C.③④ D.①②③④
二、填空题(本大题共 8 小题,每小题 3 分,共 24 分)
11.一个 n 边形的每个外角都是 45°,则这个 n 边形的内角和是 .
12.如图-9,现给出下列条件:①∠1=∠B;②∠2=∠5;③∠3=∠4;④∠BCD+
∠D=180°.其中能够得到 AB∥CD 的是 .(填序号)
图-9
13.如图-10,AB∥CD,直线 EF 与 AB,CD 分别交于 M,N 两点,将一个含有 45°角 的三角尺按图中所示的方式摆放.若∠EMB=75°,则∠PNM 的度数为 .
图-10
14.一个三角形两边的长分别为 3 和 6 ,若第三边长为奇数,则此三角形的周长为
。
15.在△ABC 中,若∠A= ∠B= ∠C,则∠A= °,△ABC 是 三角形.
16.某中学校园内有一块长 30 m,宽 22 m 的长方形草坪,中间有两条宽 2 m 的小路,
把草坪分成了 4 块,如图-11 所示,则草坪的面积为 .
图-11
17.如果一个多边形的内角和为 1620°,那么过这个多边形的一个顶点可以画
条对角线.
18.如图-12 所示,∠A+∠B+∠C+∠D+∠E+∠F= °.
图-12
三、解答题(共 46 分)
19.(6 分)如图-13,在网格纸中(每个小正方形的边长均为 1),将格点三角形 ABC 经过 一次平移后得到△A′B′C′,图中标出了点 B 的对应点 B′.
(1)补全△A′B′C′;
(2)连接 AA′,BB′,则线段 AA′与 BB′的数量关系是 ,位置关系是 ;
(3)求△A′B′C′的面积.
图-13
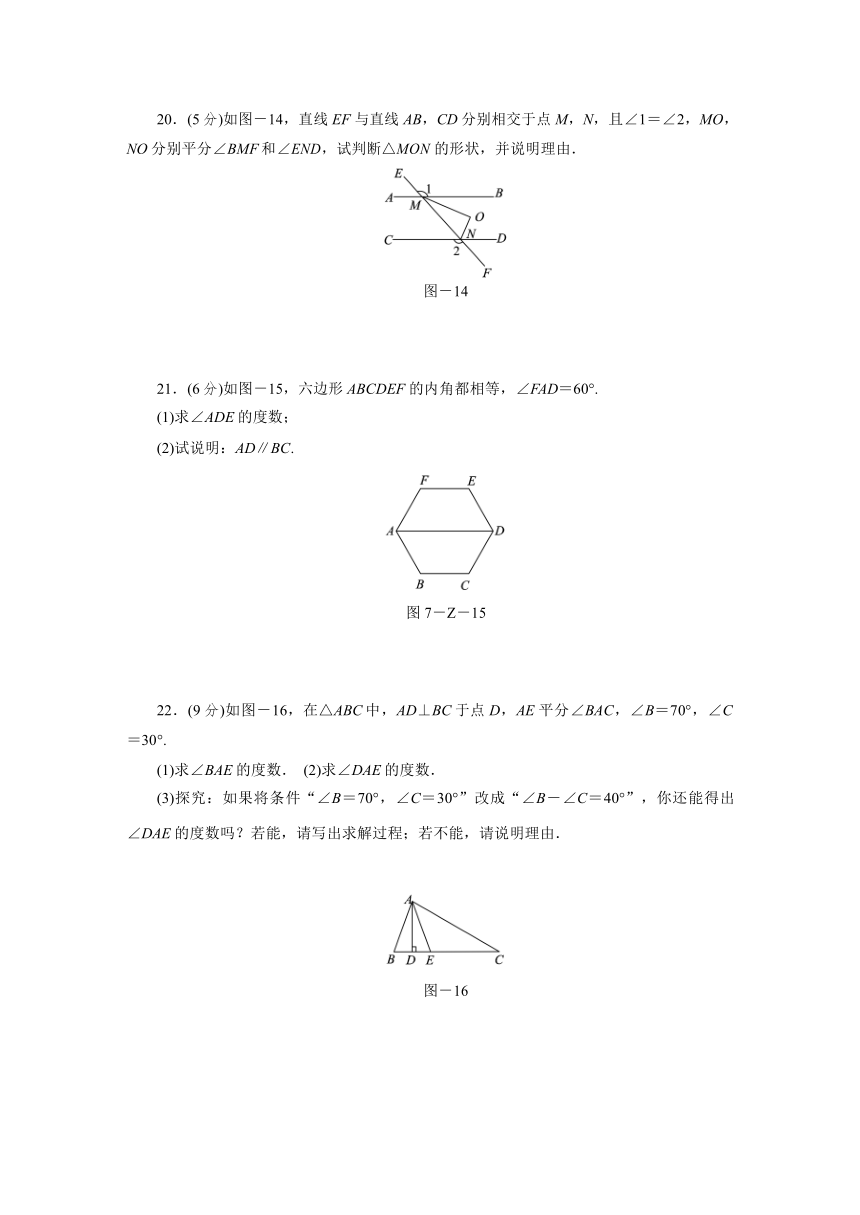
20.(5 分)如图-14,直线 EF 与直线 AB,CD 分别相交于点 M,N,且∠1=∠2,MO,
NO 分别平分∠BMF 和∠END,试判断△MON 的形状,并说明理由.
图-14
21.(6 分)如图-15,六边形 ABCDEF 的内角都相等,∠FAD=60°. (1)求∠ADE 的度数;
(2)试说明:AD∥BC.
图 7-Z-15
22.(9 分)如图-16,在△ABC 中,AD⊥BC 于点 D,AE 平分∠BAC,∠B=70°,∠C
=30°.
(1)求∠BAE 的度数. (2)求∠DAE 的度数.
(3)探究:如果将条件“∠B=70°,∠C=30°”改成“∠B-∠C=40°”,你还能得出
∠DAE 的度数吗?若能,请写出求解过程;若不能,请说明理由.
图-16
23.(10 分)如图,已知 AB∥CD,现将一直角三角形 PMN 放入图中,其中∠P=90°,PM 交
AB 于点 E,PN 交 CD 于点 F.
(1)当三角形 PMN 所放位置如图①所示时,则∠PFD 与∠AEM 的数量关系是
.
(2)当三角形 PMN 所放位置如图②所示时,求证:∠PFD —∠AEM =90°.
(3)在(2)的条件下,若 MN 与 CD 交于点 O,且∠DON=30°,∠PEB=15°,求∠N 的度 数.
24.(10 分)(1)如图 1,∠MON=70°,点 A、B 分别在射线 OM、ON 上移动,△AOB 的角 平分线 AC 与 BD 交于点 P.试问:随着点 A、B 位置的变化,∠APB 的大小是 否会变化?若保持不变,请求出∠APB 的度数.若发生变化,求出变化范围.
(2)如图 2,画两条相交的直线 OX、OY,使∠XOY=60°,① 在射线 OX、OY 上分别再任 意取 A、B 两点,② 作∠ABY 的平分线 BD,BD 的反向延长线交∠OAB 的平分线于
点 C,随着点 A、B 位置的变化,∠C 的大小是否会变化?若保持不变,请求出∠C 的
度数.若发生变化,求出变化范围.
教师详解详析
1.[解析] C 根据同旁内角的定义,图中与∠B 是同旁内角的角有 3 个,分别是∠BAC,
∠BEF,∠ACB.故选 C.
2.D
3.B
4.[解析] C n 边形的内角和为(n-2)×180°,所以设边数为 n,可列方程(n-2)×180=
108n,解得 n=5.
5.[解析] C 因为把△ABC 沿 BC 的方向平移到△DEF 的位置,BC=5,∠A=70°,∠
B=75°,
所以 CF=BE=3,∠F=∠ACB=180°-∠A-∠B=180°-70°-75°=35°,AB∥DE,
所以 A,B,D 正确,C 错误.故选 C.
6.[解析] C 因为 AD 是△ABC 的中线,△ABC 的面积为 10,所以 S△ADC= S△ABC=×10=5.因为 DE 是△ADC 的中线,所以S△ADE = S△ADC=×5=2.5.故选 C.
7.[解析] B 因为 l1∥AB, 所以∠2=∠4,∠3=∠2,∠5=∠1+∠2. 因为 AC 为角平分线,所以∠1=∠2 所以∠1=∠2=∠4=∠3,∠5=2∠1.故选 B.
8.[解析] C 根据图形知,AD 是△ABC 中 BC 边上的高.故选 C.
9.[解析] C 因为 AB∥OC,∠A=60°, 所以∠A+∠AOC=180°, 所以∠AOC=120°,
所以∠BOC=120°-90°=30°,所以∠OEC=180°-∠C-∠BOC=180°-45°-30°=
105°,所以∠DEO=180°-∠OEC=75°.故选 C.
10.[解析] A 因为∠B=∠C,所以 AB∥CD, 所以∠A=∠AEC. 又因为∠A=∠D,所以∠AEC=∠D,
所以 AE∥DF,所以∠AMC=∠FNM. 又因为∠BND=∠FNM,所以∠AMC=∠BND,故①②④正确. 由条件不能得出∠AMC=90°,故③不一定正确.故选 A.
11.[答案] 1080°
[解析] 多边形的边数是 360÷45=8,则多边形的内角和是(8-2)×180=1080°.
12.①②
13.[答案] 30°
[解析] 因为 AB∥CD, 所以∠DNM=∠EMB=75°.因为∠PND=45°,所以∠PNM=∠DNM-∠PND=30°.
14.[答案] 14 或 16
[解析] 根据三角形的三边关系可得:6-3<第三边长<6+3, 即 3<第三边长<9.
因为第三边长取奇数, 所以第三边长是 5 或 7,
所以三角形的周长为 14 或 16.
15.[答案] 30 直角
[解析] 因为∠A= ∠B= ∠C
所以可以假设∠A=x,∠B=2x,∠C=3x. 因为∠A+∠B+∠C=180°,所以 6x=180°, 所以 x=30°,
所以∠A=30°,∠C=90°,
所以△ABC 是直角三角形.故答案为 30,直角.
16.[答案] 560 m2
[解析] (30-2)×(22-2)=560(m2).
17.[答案] 8
[解析] 设此多边形的边数为 x.由题意, 得(x-2)×180°=1620°,解得 x=11. 从这个多边形的一个顶点出发所画的对角线条数为 11-3=8.
18.360
19.解:(1)如图所示,△A′B′C′即为所求.
(2)相等 平行
(3)△A′B′C′的面积为1×4×4=8.
2
20.解:△MON 是直角三角形. 理由:因为∠1=∠2,∠2=∠END, 所以∠1=∠END,
所以 AB∥CD, 所以∠BMF+∠END=180°.
因为 MO,NO 分别平分∠BMF 和∠END,
所以∠OMN+∠ONM= (∠BMF+∠END)=90°,
所以∠O=180°-(∠OMN+∠ONM)=90°, 所以△MON 是直角三角形.
21.解:(1)因为六边形 ABCDEF 的内角都相等, 所以∠BAF=∠B=∠C=∠CDE=∠E=∠F=120°. 因为∠FAD=60°,
所以∠F+∠FAD=180°, 所以 EF∥AD, 所以∠E+∠ADE=180°, 所以∠ADE=60°. (2)因为∠BAD=∠BAF-∠FAD=60°, 所以∠BAD+∠B=180°,所以 AD∥BC.
22.解:(1)因为∠B+∠C+∠BAC=180°, 所以∠BAC=180°-∠B-∠C=180°-70°-30°=80°. 因为 AE 平分∠BAC,
所以∠BAE=∠BAC=40°.
(2)因为 AD⊥BC,
所以∠ADB=90°,
所以∠B+∠BAD=90°, 则∠BAD=90°-∠B=90°-70°=20°, 所以∠DAE=∠BAE-∠BAD=40°-20°=20°. (3)能.
因为∠B+∠C+∠BAC=180°,
所以∠BAC=180°-∠B-∠C.
因为 AE 平分∠BAC,
所以∠BAE=∠BAC=(180°-∠B-∠C)=90°-(∠B+∠C)
1
因为 AD⊥BC,所以∠ADB=90°,
所以∠B+∠BAD=90°,
则∠BAD=90°-∠B,
所以∠DAE=∠BAE-∠BAD=90°-(∠B+∠C)-(90°-∠B)=(∠B-∠C).
因为∠B-∠C=40°,
所以∠DAE=×40°=20°.
23.
24.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
