人教版九年级数学下册 28.1 锐角三角函数 课件(共64张PPT)
文档属性
| 名称 | 人教版九年级数学下册 28.1 锐角三角函数 课件(共64张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览










文档简介
(共64张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
问题1 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是 30°,为使出水口的高度为 35 m,需要准备多长的水管?
这个问题可以归结为:
在 Rt△ABC 中,∠C=90°,∠A=30°,BC=35 m,
求 AB.
C
B
A
提出问题
28.1 锐角三角函数
人教版八年级数学 下册
目标导航
1.初步理解在直角三角形中正弦函数、余弦函数、正切函数的定义。
2.会求解简单的锐角三角函数。
认真阅读课本28.1 锐角三角函数的内容,完成下面练习并体验知识点的形成过程.
自主研学
目标导航一
正弦及应用
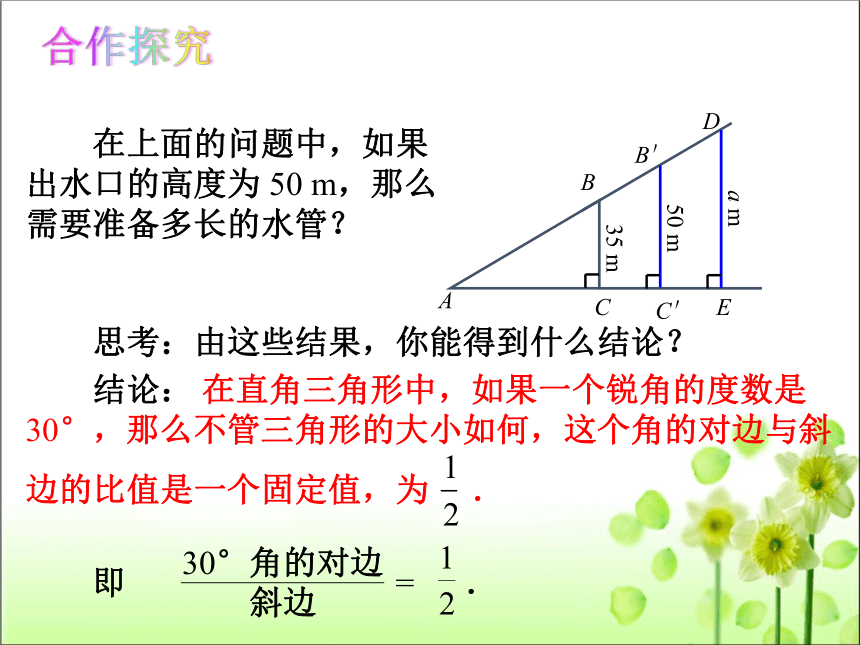
在上面的问题中,如果出水口的高度为 50 m,那么需要准备多长的水管?
C'
思考:由这些结果,你能得到什么结论?
结论: 在直角三角形中,如果一个锐角的度数是30°,那么不管三角形的大小如何,这个角的对边与斜
边的比值是一个固定值,为 .
A
B
C
50 m
35 m
B'
a m
D
E
30°角的对边
斜边
即 = .
合作探究
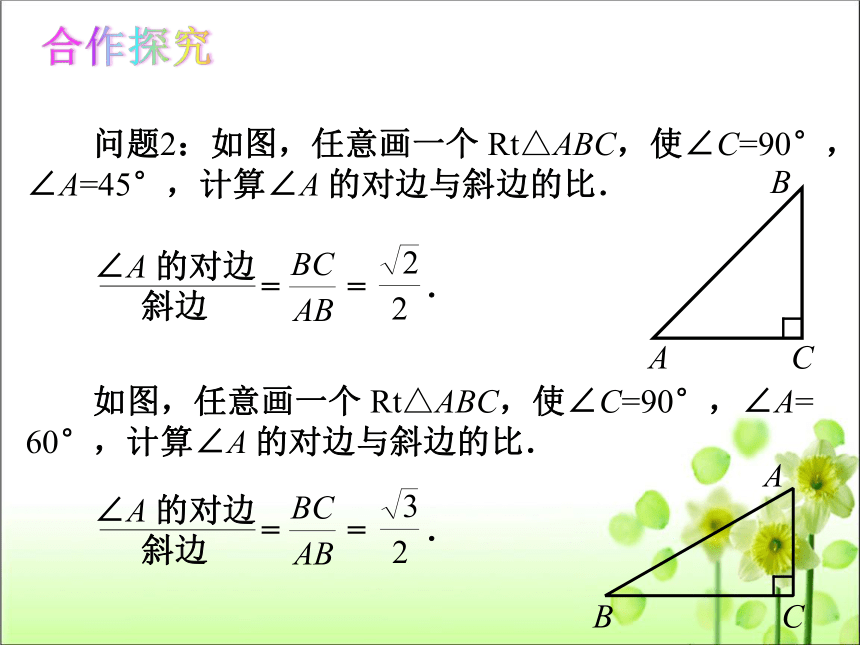
问题2:如图,任意画一个 Rt△ABC,使∠C=90°,
∠A=45°,计算∠A 的对边与斜边的比.
A
B
C
如图,任意画一个 Rt△ABC,使∠C=90°,∠A=
60°,计算∠A 的对边与斜边的比.
A
B
C
∠A 的对边
斜边
= = .
∠A 的对边
斜边
= = .
合作探究
在直角三角形中,如果一个锐角的度数是 45°,那么不管三角形的大小如何,这个角的对边与斜边的比是
一个固定值,为 .
45°角的对边
斜边
即 = .
在直角三角形中,如果一个锐角的度数是 60°,那么不管三角形的大小如何,这个角的对边与斜边的比是
一个固定值,为 .
60°角的对边
斜边
即 = .
合作探究
1、在Rt△ABC中,∠C为直角,AC=4,BC=3,则sinA=( )
A. ; B. ; C. ; D. .
2、已知sinA= (∠A为锐角),则∠A= .
C
30°
即学即练
问题3 任意画 Rt△ABC 和 Rt△ ,使得
∠C =∠C'=90°.∠A=∠A',那么 与 有什
么关系.你能解释一下吗?
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,它的对边与斜边的比是一个固定值.
解:∵ ∠C= ∠C'=90°,∠A=∠A'.
∴ Rt △ABC ∽Rt △ .
∴ = .
∴ = .
A'
C'
B'
A
C
B
'
'
A B
'
'
B C
'
'
'
A B C
'
'
'
A B C
'
'
B C
BC
'
'
A B
'
'
B C
'
'
A B
AB
合作探究
在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sin A,即
∠A 的正弦 sin A 随着∠A 的 变化而变化.
A
C
B
∠A 的对边
斜边
sin A= = .
斜边 c
对边
a
sin 30°= ;
sin 45°= ;
sin 60°= .
b
合作探究
例 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
解: (1)在Rt△ABC中,
因此
(2)在Rt△ABC中,
因此
A
B
C
A
B
C
3
4
13
求sinA就是要确定∠A的对边与斜边的比;求sinB就是要确定∠B的对边与斜边的比
5
合作探究
1.判断对错:
A
10m
6m
B
C
1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√
√
×
×
sinA是一个比值(注意比的顺序),无单位;
2)如图,sinA= ( )
×
即学即练
2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定
C
3.如图
A
C
B
3
7
30°
则 sinA=______ .
1
2
即学即练
3、如下三幅图,在 Rt△ABC 中,∠C=90°,求 sin A 和 sin B 的值.
图(1) 图(2) 图(3)
B
A
C
3
4
A
A
B
B
C
C
2
6
即学即练
1、锐角A的对边与斜边的比叫做 ,
记作 .
∠A 的正弦
sinA
2、sin30°=______; sin45°=______.
归纳小结
1、在Rt△ABC中,∠C=90°,AB=10,sinA= ,则BC的长为_____.
2、当锐角A>45°时,sinA的值( )
A、小于 B、大于
C、小于 D、大于
8
B
检测目标
2、判断下列结论是否正确,并说明理由.
(1)在 Rt△ABC 中,锐角 A 的对边和斜边同时扩大 100 倍,sin A 的值也扩大 100 倍;
(2)如图所示,△ABC 的
顶点是正方形网格的格点,则
sin B= = .
C
B
A
D
E
F
检测目标
3、在Rt△ABC中,∠C为直角,∠A=30°,AB=4,求sinB的值.
解:∵在△ABC中,∠C为直角,∠A=30°,AB=4
∴ ,
∴
∴sinB= = =
检测目标
目标导航二
余弦和正切
1、一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值, y都有唯一确定的值与其对应,那么我们称y是x的________
函数
知识回顾
2、分别求出图中∠A,∠B的正弦值.
sinA=
sinB=
sinA=
sinA=
sinB=
sinB=
知识回顾
请同学们回顾一下,什么是正弦?
在 Rt△ABC 中,∠C=90°,当∠A 确定时,∠A 的对边与斜边比随之确定.此时,其他边之间的比是否也随之确定呢?
知识回顾
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?
A
B
C
邻边b
对边a
斜边c
当锐角A的大小确定时,∠A的邻边与斜边的比我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即
cosA=
—————
斜边
∠A的邻边
合作探究
1、sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA是一个比值(数值)。
3、sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
如图:在Rt △ABC中,∠C=90°,
正弦
余弦
当直角三角形的一个锐角的大小确定时,其对边与邻边比值也是惟一确定的吗?
合作探究
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。
BC
B′C′
A′C′
AC
=
=
所以
AC
BC
A′C′
B′C′
=
即
AC
BC
A′C′
B′C′
=
问:
有什么关系?
如图,Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,∠A=∠A′=α,
由于∠C=∠C′=90°,∠A=∠A′=α,
所以Rt△ABC ∽ Rt△A′B′C′
合作探究
1、在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比叫做_______________,
记作______,即_______=_ _=
把∠A的对边与邻边的比叫做___________,
记作________,即___________________=__.
∠A的余弦
cosA
∠A的邻边
∠A的正切
tanA
tanA=
—————
斜边
∠A的对边
—————————
∠A的邻边
cosA
归纳总结
2、对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,_____,______也是A的函数.
3、锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
cosA
tanA
正弦
余弦
正切
归纳总结
1、在Rt△ABC中,∠C为直角,a=1,b=2,
则cosA=________ ,tanA=_________.
2、在Rt△ABC中,各边都扩大四倍,则锐角A的各三角函数值( )
A.没有变化 B.分别扩大4倍
C.分别缩小到原来的 D.不能确定
A
即学即练
如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求 sin A,cos A,tan A 的值.
解:在 Rt△ABC 中,AC= =8.
sin A= = ;
cos A= = ;
tan A= = .
6
C
A
10
B
巩固概念
A
C
B
在 Rt△ABC 中,∠C=90°,∠A=30°,
求:cos 30°,tan 30°.
tan 30°= = .
AC
BC
解:在 Rt△ABC 中,
cos 30°= = .
AB
AC
经验类比
锐角 A
锐角三角函数 30° 45° 60°
sin A
cos A
tan A
探究:类比推导 30°角的三角函数值的方法,你能推导 45°,60°角的三角函数值吗?
1
经验类比
下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
即学即练
如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
即学即练
1、在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比叫做____________________,
记作______,即___________________=___;
把∠A的对边与邻边的比叫做___________,
记作________,即___________________=__.
∠A的余弦
cosA
∠A的邻边
∠A的正切
tanA
tanA=
—————
斜边
∠A的对边
————
∠A的邻边
归纳小结
cosA=
2、对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,_____,______也是A的函数.
3、锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
cosA
tanA
正弦
余弦
正切
归纳小结
=
a
c
sinA=
在Rt△ABC中
及时总结经验,要养成积累方法和经验的良好习惯!
=
b
c
cosA=
=
a
b
tanA=
归纳小结
定义中应该注意的几个问题:
1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
归纳小结
目标导航三
求锐角三角函数值
1.画出三角形,通过测量估算 sin A 的值.
2.这样计算有哪些缺陷?还有其他更好的方法吗?
新知探究
认真阅读课本内容,完成
下面练习,并体验知识点的形成过程.
阅读自己计算器的使用说明,懂得操作步
骤.
例 用计算器求下列锐角三角函数值:
知识点一用计算器求下列锐角三角函数值
sin18°=_________tan30°36=_______
tan30.6°=_________
练一练 用计算器求下列锐角三角函数值(保留四个有效数字).
Sin57°=______ tan59°14′=_______
0.309016994
0.591398351
0.591398351
0.8387
1.680
自主研学
已知下列锐角三角函数值,用计算器求其
相应的锐角:
已知sinA=0.5018,求∠A的度数.
知识点二 根据已知锐角三角函数值用计算器求其相应的锐角
你怎验算答案是否正确?
依次按键 ,然后输入函数值0.5018,得到∠A=30.11915867°(这说明锐角A精确到1°的结果为30°)
2nd F
sin
使用锐角三角函数表,也可以
查得锐角的三角函数值,或根据锐角
三角函数值求相应的锐角。
合作探究
例1.用计算器求下列三角函数值(精确到
0.000 1):
(1)sin 36°;
(2)tan 50° .
1.用计算器求锐角的三角函数值时应首先按哪一个键?
思考:
2.怎样用计算器求锐角的三角函数值?要注意什么问题?
26′
37″
典型例题
例2.已知三角函数值,求锐角(精确到 1″):
(1)已知 cos α =0.523 7,求锐角α;
(2)已知 tan β =1.648 0,求锐角β.
怎样使用计算器由锐角三角函数值求锐角?要注意什么问题?
思考:
合作探究
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
合作探究
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
合作探究
设两条直角边长为a,则斜边长=
60°
45°
合作探究
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数 30° 45° 60°
sin a
cos a
tan a
仔细观察,说说你发现这张表有哪些规律?
合作探究
用计算器求下列各式中的锐角(精确到分).
Sinα=0.536,α=_________
cosα=0.1842,α=_________
32°25′
79°23′
即学即练
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
即学即练
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
即学即练
1、我们可以用计算器求锐角三角函数值.
2、已知下列锐角三角函数值,可以用计算器求
其相应的锐角.
3、学习反思:______________________
______________________________________________________________________________
课堂小结
1、下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15°
B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15°
D. sin75°﹤sin48°﹥sin15°
2、不查表,比较大小:
(1)sin20.3°______sin20°15′;
(2)cos51°______cos50°10′;
(3)sin21°______cos68°.
3、锐角α的正弦函数值随α的增大而____,
锐角α的余弦函数值,随α的增大而_____
>
<
<
A
增大
减小
检测目标
2、sin0°=0,sin90°=1.利用计算器求sin57°与cos33° ,所
得的值有什么关系?
解:∵sin57°= 0.838670567945
cos33°= 0.838670567945
∴ sin57°= cos33°
检测目标
3、如图,要焊接一个高3.5米,底角为32°
的人字形钢架,约需多长的钢材(结果保
留小数点后两位)?
解:依题意可知,AC=BC AD=BD 在RT△CDA中
∵AC=CDsin32°=3.5× 0.530 =1.855
AD=CDtan32°=3.5×0.625
=2.188
∴AC+BC+AD+DB+CD
=2AC+2AD+CD
=2×1.855+2×2.188+3.5
=3.710+4.376+3.5
=11.586 ≈11.59(米)
答:约需11.59米的钢材
检测目标
4、Rt△ABC中,∠C=90°,如果AB=2,BC=1,那么cosB的值为( )
A、 B、 C、 D、
5、在Rt?ABC中,∠C=90°,如果cos A= 那么tanB的值为( )
A、 B、 C、 D、
A
D
检测目标
6、如图,PA是圆O切线,A为切点,PO交圆O于点B,PA=8,OB=6,求tan∠APO的值.
解:∵ PA是圆O的切线
∴ PA⊥OA
∴ ?POA是直角三角形
又∵ OA=OB
∴
检测目标
7、操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
?
你想知道小明怎样算出的吗?
30°
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
问题1 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是 30°,为使出水口的高度为 35 m,需要准备多长的水管?
这个问题可以归结为:
在 Rt△ABC 中,∠C=90°,∠A=30°,BC=35 m,
求 AB.
C
B
A
提出问题
28.1 锐角三角函数
人教版八年级数学 下册
目标导航
1.初步理解在直角三角形中正弦函数、余弦函数、正切函数的定义。
2.会求解简单的锐角三角函数。
认真阅读课本28.1 锐角三角函数的内容,完成下面练习并体验知识点的形成过程.
自主研学
目标导航一
正弦及应用
在上面的问题中,如果出水口的高度为 50 m,那么需要准备多长的水管?
C'
思考:由这些结果,你能得到什么结论?
结论: 在直角三角形中,如果一个锐角的度数是30°,那么不管三角形的大小如何,这个角的对边与斜
边的比值是一个固定值,为 .
A
B
C
50 m
35 m
B'
a m
D
E
30°角的对边
斜边
即 = .
合作探究
问题2:如图,任意画一个 Rt△ABC,使∠C=90°,
∠A=45°,计算∠A 的对边与斜边的比.
A
B
C
如图,任意画一个 Rt△ABC,使∠C=90°,∠A=
60°,计算∠A 的对边与斜边的比.
A
B
C
∠A 的对边
斜边
= = .
∠A 的对边
斜边
= = .
合作探究
在直角三角形中,如果一个锐角的度数是 45°,那么不管三角形的大小如何,这个角的对边与斜边的比是
一个固定值,为 .
45°角的对边
斜边
即 = .
在直角三角形中,如果一个锐角的度数是 60°,那么不管三角形的大小如何,这个角的对边与斜边的比是
一个固定值,为 .
60°角的对边
斜边
即 = .
合作探究
1、在Rt△ABC中,∠C为直角,AC=4,BC=3,则sinA=( )
A. ; B. ; C. ; D. .
2、已知sinA= (∠A为锐角),则∠A= .
C
30°
即学即练
问题3 任意画 Rt△ABC 和 Rt△ ,使得
∠C =∠C'=90°.∠A=∠A',那么 与 有什
么关系.你能解释一下吗?
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,它的对边与斜边的比是一个固定值.
解:∵ ∠C= ∠C'=90°,∠A=∠A'.
∴ Rt △ABC ∽Rt △ .
∴ = .
∴ = .
A'
C'
B'
A
C
B
'
'
A B
'
'
B C
'
'
'
A B C
'
'
'
A B C
'
'
B C
BC
'
'
A B
'
'
B C
'
'
A B
AB
合作探究
在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sin A,即
∠A 的正弦 sin A 随着∠A 的 变化而变化.
A
C
B
∠A 的对边
斜边
sin A= = .
斜边 c
对边
a
sin 30°= ;
sin 45°= ;
sin 60°= .
b
合作探究
例 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
解: (1)在Rt△ABC中,
因此
(2)在Rt△ABC中,
因此
A
B
C
A
B
C
3
4
13
求sinA就是要确定∠A的对边与斜边的比;求sinB就是要确定∠B的对边与斜边的比
5
合作探究
1.判断对错:
A
10m
6m
B
C
1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√
√
×
×
sinA是一个比值(注意比的顺序),无单位;
2)如图,sinA= ( )
×
即学即练
2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定
C
3.如图
A
C
B
3
7
30°
则 sinA=______ .
1
2
即学即练
3、如下三幅图,在 Rt△ABC 中,∠C=90°,求 sin A 和 sin B 的值.
图(1) 图(2) 图(3)
B
A
C
3
4
A
A
B
B
C
C
2
6
即学即练
1、锐角A的对边与斜边的比叫做 ,
记作 .
∠A 的正弦
sinA
2、sin30°=______; sin45°=______.
归纳小结
1、在Rt△ABC中,∠C=90°,AB=10,sinA= ,则BC的长为_____.
2、当锐角A>45°时,sinA的值( )
A、小于 B、大于
C、小于 D、大于
8
B
检测目标
2、判断下列结论是否正确,并说明理由.
(1)在 Rt△ABC 中,锐角 A 的对边和斜边同时扩大 100 倍,sin A 的值也扩大 100 倍;
(2)如图所示,△ABC 的
顶点是正方形网格的格点,则
sin B= = .
C
B
A
D
E
F
检测目标
3、在Rt△ABC中,∠C为直角,∠A=30°,AB=4,求sinB的值.
解:∵在△ABC中,∠C为直角,∠A=30°,AB=4
∴ ,
∴
∴sinB= = =
检测目标
目标导航二
余弦和正切
1、一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值, y都有唯一确定的值与其对应,那么我们称y是x的________
函数
知识回顾
2、分别求出图中∠A,∠B的正弦值.
sinA=
sinB=
sinA=
sinA=
sinB=
sinB=
知识回顾
请同学们回顾一下,什么是正弦?
在 Rt△ABC 中,∠C=90°,当∠A 确定时,∠A 的对边与斜边比随之确定.此时,其他边之间的比是否也随之确定呢?
知识回顾
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?
A
B
C
邻边b
对边a
斜边c
当锐角A的大小确定时,∠A的邻边与斜边的比我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即
cosA=
—————
斜边
∠A的邻边
合作探究
1、sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA是一个比值(数值)。
3、sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
如图:在Rt △ABC中,∠C=90°,
正弦
余弦
当直角三角形的一个锐角的大小确定时,其对边与邻边比值也是惟一确定的吗?
合作探究
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。
BC
B′C′
A′C′
AC
=
=
所以
AC
BC
A′C′
B′C′
=
即
AC
BC
A′C′
B′C′
=
问:
有什么关系?
如图,Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,∠A=∠A′=α,
由于∠C=∠C′=90°,∠A=∠A′=α,
所以Rt△ABC ∽ Rt△A′B′C′
合作探究
1、在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比叫做_______________,
记作______,即_______=_ _=
把∠A的对边与邻边的比叫做___________,
记作________,即___________________=__.
∠A的余弦
cosA
∠A的邻边
∠A的正切
tanA
tanA=
—————
斜边
∠A的对边
—————————
∠A的邻边
cosA
归纳总结
2、对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,_____,______也是A的函数.
3、锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
cosA
tanA
正弦
余弦
正切
归纳总结
1、在Rt△ABC中,∠C为直角,a=1,b=2,
则cosA=________ ,tanA=_________.
2、在Rt△ABC中,各边都扩大四倍,则锐角A的各三角函数值( )
A.没有变化 B.分别扩大4倍
C.分别缩小到原来的 D.不能确定
A
即学即练
如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求 sin A,cos A,tan A 的值.
解:在 Rt△ABC 中,AC= =8.
sin A= = ;
cos A= = ;
tan A= = .
6
C
A
10
B
巩固概念
A
C
B
在 Rt△ABC 中,∠C=90°,∠A=30°,
求:cos 30°,tan 30°.
tan 30°= = .
AC
BC
解:在 Rt△ABC 中,
cos 30°= = .
AB
AC
经验类比
锐角 A
锐角三角函数 30° 45° 60°
sin A
cos A
tan A
探究:类比推导 30°角的三角函数值的方法,你能推导 45°,60°角的三角函数值吗?
1
经验类比
下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
即学即练
如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
即学即练
1、在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比叫做____________________,
记作______,即___________________=___;
把∠A的对边与邻边的比叫做___________,
记作________,即___________________=__.
∠A的余弦
cosA
∠A的邻边
∠A的正切
tanA
tanA=
—————
斜边
∠A的对边
————
∠A的邻边
归纳小结
cosA=
2、对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,_____,______也是A的函数.
3、锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
cosA
tanA
正弦
余弦
正切
归纳小结
=
a
c
sinA=
在Rt△ABC中
及时总结经验,要养成积累方法和经验的良好习惯!
=
b
c
cosA=
=
a
b
tanA=
归纳小结
定义中应该注意的几个问题:
1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
归纳小结
目标导航三
求锐角三角函数值
1.画出三角形,通过测量估算 sin A 的值.
2.这样计算有哪些缺陷?还有其他更好的方法吗?
新知探究
认真阅读课本内容,完成
下面练习,并体验知识点的形成过程.
阅读自己计算器的使用说明,懂得操作步
骤.
例 用计算器求下列锐角三角函数值:
知识点一用计算器求下列锐角三角函数值
sin18°=_________tan30°36=_______
tan30.6°=_________
练一练 用计算器求下列锐角三角函数值(保留四个有效数字).
Sin57°=______ tan59°14′=_______
0.309016994
0.591398351
0.591398351
0.8387
1.680
自主研学
已知下列锐角三角函数值,用计算器求其
相应的锐角:
已知sinA=0.5018,求∠A的度数.
知识点二 根据已知锐角三角函数值用计算器求其相应的锐角
你怎验算答案是否正确?
依次按键 ,然后输入函数值0.5018,得到∠A=30.11915867°(这说明锐角A精确到1°的结果为30°)
2nd F
sin
使用锐角三角函数表,也可以
查得锐角的三角函数值,或根据锐角
三角函数值求相应的锐角。
合作探究
例1.用计算器求下列三角函数值(精确到
0.000 1):
(1)sin 36°;
(2)tan 50° .
1.用计算器求锐角的三角函数值时应首先按哪一个键?
思考:
2.怎样用计算器求锐角的三角函数值?要注意什么问题?
26′
37″
典型例题
例2.已知三角函数值,求锐角(精确到 1″):
(1)已知 cos α =0.523 7,求锐角α;
(2)已知 tan β =1.648 0,求锐角β.
怎样使用计算器由锐角三角函数值求锐角?要注意什么问题?
思考:
合作探究
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
合作探究
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
合作探究
设两条直角边长为a,则斜边长=
60°
45°
合作探究
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数 30° 45° 60°
sin a
cos a
tan a
仔细观察,说说你发现这张表有哪些规律?
合作探究
用计算器求下列各式中的锐角(精确到分).
Sinα=0.536,α=_________
cosα=0.1842,α=_________
32°25′
79°23′
即学即练
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
即学即练
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
即学即练
1、我们可以用计算器求锐角三角函数值.
2、已知下列锐角三角函数值,可以用计算器求
其相应的锐角.
3、学习反思:______________________
______________________________________________________________________________
课堂小结
1、下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15°
B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15°
D. sin75°﹤sin48°﹥sin15°
2、不查表,比较大小:
(1)sin20.3°______sin20°15′;
(2)cos51°______cos50°10′;
(3)sin21°______cos68°.
3、锐角α的正弦函数值随α的增大而____,
锐角α的余弦函数值,随α的增大而_____
>
<
<
A
增大
减小
检测目标
2、sin0°=0,sin90°=1.利用计算器求sin57°与cos33° ,所
得的值有什么关系?
解:∵sin57°= 0.838670567945
cos33°= 0.838670567945
∴ sin57°= cos33°
检测目标
3、如图,要焊接一个高3.5米,底角为32°
的人字形钢架,约需多长的钢材(结果保
留小数点后两位)?
解:依题意可知,AC=BC AD=BD 在RT△CDA中
∵AC=CDsin32°=3.5× 0.530 =1.855
AD=CDtan32°=3.5×0.625
=2.188
∴AC+BC+AD+DB+CD
=2AC+2AD+CD
=2×1.855+2×2.188+3.5
=3.710+4.376+3.5
=11.586 ≈11.59(米)
答:约需11.59米的钢材
检测目标
4、Rt△ABC中,∠C=90°,如果AB=2,BC=1,那么cosB的值为( )
A、 B、 C、 D、
5、在Rt?ABC中,∠C=90°,如果cos A= 那么tanB的值为( )
A、 B、 C、 D、
A
D
检测目标
6、如图,PA是圆O切线,A为切点,PO交圆O于点B,PA=8,OB=6,求tan∠APO的值.
解:∵ PA是圆O的切线
∴ PA⊥OA
∴ ?POA是直角三角形
又∵ OA=OB
∴
检测目标
7、操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
?
你想知道小明怎样算出的吗?
30°
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
