北师大版七年级数学下册 1.2.1幂的乘方课件 (22张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 1.2.1幂的乘方课件 (22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 22:19:42 | ||
图片预览








文档简介
(共22张PPT)
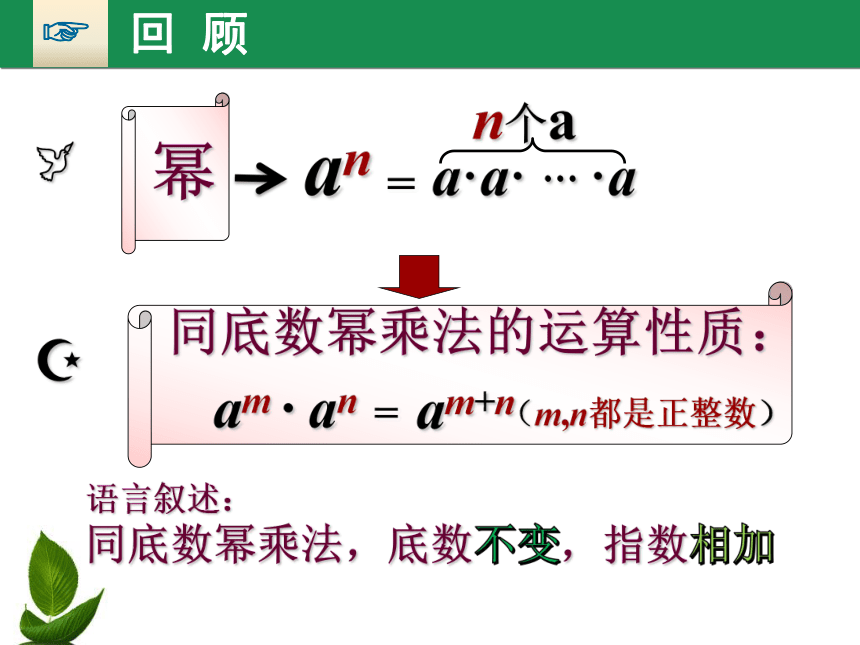
(am)n
回顾与思考
?
幂
an
=
am+n
(m,n都是正整数)
回 顾
?
练 习
计算 (1)
(2)
am ·am = .
102×104 = .
62×62×62= .
(3)
思考:
做一做
根据乘方的定义及同底数幂的乘法性质,完成下列各题。
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ;
解:(1) (62)4
(2) (a2)3
(3) (am)2
=62· 62·62· 62
=62+2+2+2
=68
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
amn
(4) (am)n
(am)n
=amn
(am)n=amn (m,n都是正整数).
底数 ,
不变
相乘
幂的乘方,
(幂的意义)
(同底数幂的乘法性质)
(乘法的意义)
指数 .
例题解析
【例1】计算:
(103)5 (2) (a4)4
(3) (am)2 (4) -(x4)3
例题解析
计算:
(x3)2 (2) -(bm)5
(3) (a3)2·a (4) [-(y2)]3
(5) 2(a3)4-(a2)6
请比较“同底数幂相乘的法则”与“幂的乘方法则”异同:
同底数幂相乘
幂的乘方
乘法运算
乘方运算
底数不变,指数相加
底数不变,指数相乘
法则 符号语言 运算 结果
1
2
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
雁
桥
学
中
雁
x9
a8a
1
桥
-1012
x6
y3 m+3
中
b10
a5
x14
学
x4
y4m
(x+y)8
1.(2015广东)
( )
A.
B.
C.
D.
2.(2017广东)下列运算正确的是( )
A.
A. B.
C. D.
1.若am =2,则a3m = .
2.若ax =2,ay =3,则
ax +y= .
a3x +2y= .
3. 若(9n)2 = 38 ,则n = .
本节课你的收获是什么?
相乘
不变
(ab)3 = .
谢谢指导!
(am)n
回顾与思考
?
幂
an
=
am+n
(m,n都是正整数)
回 顾
?
练 习
计算 (1)
(2)
am ·am = .
102×104 = .
62×62×62= .
(3)
思考:
做一做
根据乘方的定义及同底数幂的乘法性质,完成下列各题。
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ;
解:(1) (62)4
(2) (a2)3
(3) (am)2
=62· 62·62· 62
=62+2+2+2
=68
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
amn
(4) (am)n
(am)n
=amn
(am)n=amn (m,n都是正整数).
底数 ,
不变
相乘
幂的乘方,
(幂的意义)
(同底数幂的乘法性质)
(乘法的意义)
指数 .
例题解析
【例1】计算:
(103)5 (2) (a4)4
(3) (am)2 (4) -(x4)3
例题解析
计算:
(x3)2 (2) -(bm)5
(3) (a3)2·a (4) [-(y2)]3
(5) 2(a3)4-(a2)6
请比较“同底数幂相乘的法则”与“幂的乘方法则”异同:
同底数幂相乘
幂的乘方
乘法运算
乘方运算
底数不变,指数相加
底数不变,指数相乘
法则 符号语言 运算 结果
1
2
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
雁
桥
学
中
雁
x9
a8a
1
桥
-1012
x6
y3 m+3
中
b10
a5
x14
学
x4
y4m
(x+y)8
1.(2015广东)
( )
A.
B.
C.
D.
2.(2017广东)下列运算正确的是( )
A.
A. B.
C. D.
1.若am =2,则a3m = .
2.若ax =2,ay =3,则
ax +y= .
a3x +2y= .
3. 若(9n)2 = 38 ,则n = .
本节课你的收获是什么?
相乘
不变
(ab)3 = .
谢谢指导!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
