北师版九年级数学下册 3.2《圆的对称性》 培优训练题(含答案)
文档属性
| 名称 | 北师版九年级数学下册 3.2《圆的对称性》 培优训练题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-04 00:00:00 | ||
图片预览



文档简介
北师版九年级数学下册
3.2《圆的对称性》
培优训练
一.选择题(本大题共10小题,每小题3分,共30分)
1.下列图形既是轴对称图形又是中心对称图形的是( )
2.如图,已知AB是⊙O的直径,C,D是上的三等分点,∠AOE=60°,则∠COE是( )
A.40° B.60°
C.80° D.102°
3.AB、DC是圆的两条平行弦,则四边形ABCD一定不是( )
A.等腰梯形 B.直角梯形
C.正方形 D.矩形
4. 如图,弦 AD = BC,点E是CD上任意一点(C,D除外),则下列结论不一定成立的是( )
A.=
B.AB=CD
C.AE=EB
D.=
5.如图,AB,CD分别为⊙O的两条弦,OM⊥AB于M,ON⊥CD于N,且OM=ON,则( )
A.AB=CD B.∠AOB=∠COD
C.= D.以上结论都对
6.如图,AB为⊙O的直径,C,D分别为OA,OB的中点,CF⊥AB,DE⊥AB,下列结论:①CF=DE;②==;③AE=2CF;④四边形CDEF为正方形.其中正确的是( )
A.①②③ B.①②④
C.②③④ D.①③④
7. 已知AB,CD是两个不同圆的弦,如果AB=CD,那么与的关系是( )
A.= B.>
C.< D.不能确定
8. 如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51° B.56°
C.68° D.78°
9.如图,在⊙O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD
C.AB<2CD D.以上都不正确
10. 如图,点A是半圆上一个三等分点,点B是的中点,P是直径MN上的一动点,⊙O的半径为1,则PA+PB的最小值为( )
A.1 B. C. D.-1
二.填空题(共8小题,3*8=24)
11.圆既是__________图形,又是__________图形,它有________条对称轴.
12.如图,BD是⊙O的直径,=,且∠AOB=50°,则∠AOC的度数为__________.
13.如图,矩形ABCD的四个顶点都在⊙O上,且∶=1∶2,则∠AOB=___________.
14.如图,已知AB,CD是⊙O的两条直径,CE∥AB,所对的圆心角的度数为75°,则∠BOC=______________.
15. 如图,在⊙O中,=,∠A=30°,则∠B= .
16. 如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD=_________.
17. 如图,AB和CD为⊙O的两条直径,弦CE∥AB,弧CE的度数为40°,则∠BOC= .
18. 如图,在⊙O中,点C是的中点,∠A=50°,则∠BOC=________.
三.解答题(共7小题,46分)
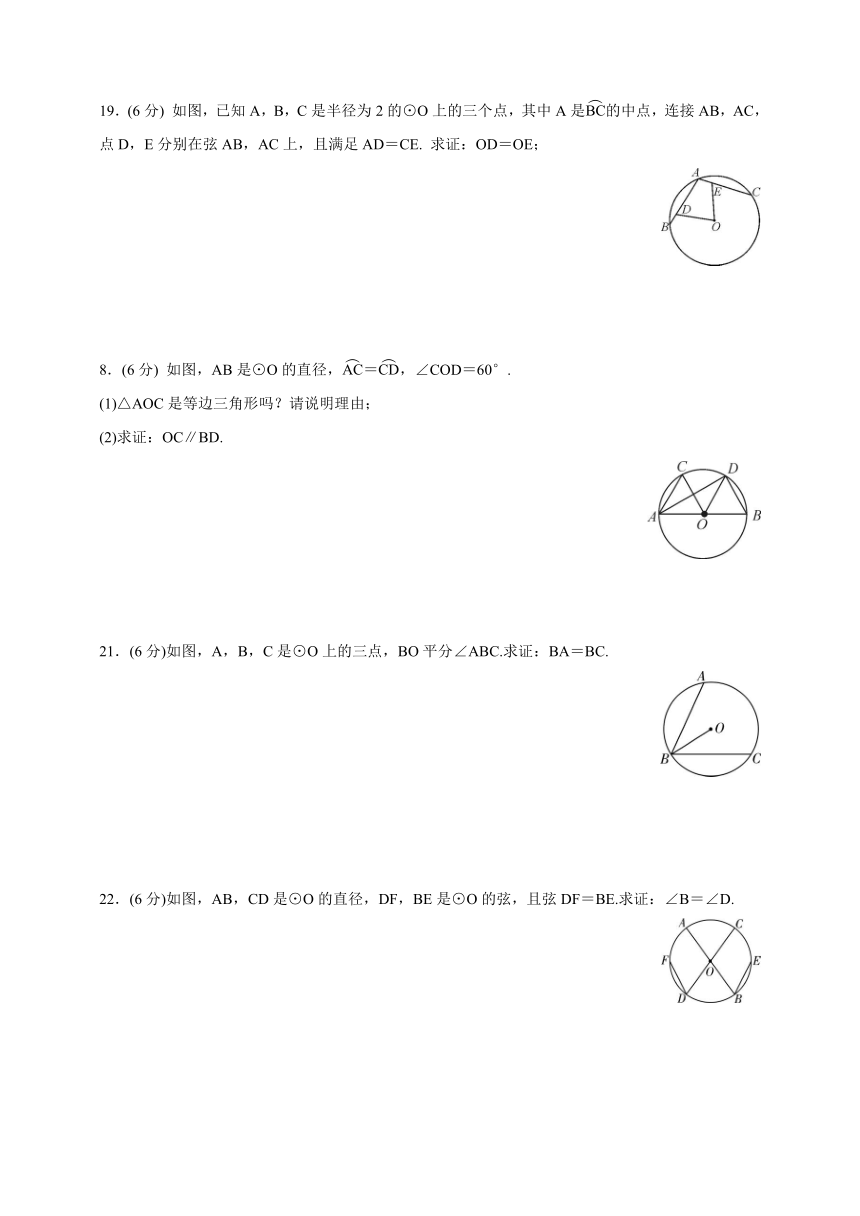
19.(6分) 如图,已知A,B,C是半径为2的⊙O上的三个点,其中A是的中点,连接AB,AC,点D,E分别在弦AB,AC上,且满足AD=CE. 求证:OD=OE;
8.(6分) 如图,AB是⊙O的直径,=,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
21.(6分)如图,A,B,C是⊙O上的三点,BO平分∠ABC.求证:BA=BC.
22.(6分)如图,AB,CD是⊙O的直径,DF,BE是⊙O的弦,且弦DF=BE.求证:∠B=∠D.
23.(6分) 如图,在⊙O中,=,点D,E分别是半径OA和OB的中点,求证:CD=CE.
24.(8分) 如图,在⊙O中,=,CD⊥OA于D,CE⊥OB于E,求证:AD=BE.
25.(8分)如图,MN是⊙O的直径,弦AB,CD相交于直线MN上的一点P,∠APM=∠CPM.
(1)如图①,根据以上条件,若交点P在⊙O的内部,试判断AB和CD的大小关系,并说明理由;
(2)如图②,若交点P要⊙O的外部,(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
参考答案:
1-5DCBCD 6-10 ADACC
11. 轴对称,中心对称,无数
12. 80°
13. 18°
14. 127.5°
15. 75°
16.40°
17. 70°
18.40°
19. 证明:连接OA,OB,OC,
∵A是的中点,∴∠AOB=∠AOC.
∵OA=OB=OC,∴∠ABO=∠BAO=∠ACO.
∵AD=CE,∴△AOD≌△COE,
∴OD=OE
8. 解:(1)△AOC是等边三角形.理由:
∵=,∴∠COA=∠COD=60°.
又∵OA=OC,∴△AOC是等边三角形
(2)由(1)得∠COA=∠COD=60°,∴∠BOD=60°.
又∵OB=OD,∴△OBD是等边三角形,
∴∠B=60°,∴∠COA=∠B,
故OC∥BD
21. 证明:如答图,连接OA,OC.
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO.
∵BO平分∠ABC,∴∠ABO=∠CBO.
∴∠BAO=∠BCO.
∴△OAB≌△OCB.
∴AB=BC.
22. 证明:∵AB,CD是⊙O的直径,∴=.
∵FD=EB,∴=.
∴-=-.
即=.∴∠D=∠B.
23. 证明:连接OC.
∵D,E分别是OA,OB的中点,
∴OD=OA,OE=OB.
∵OA=OB,∴OD=OE.
又∵=,∴∠DOC=∠EOC.
在△CDO和△CEO中,
∴△CDO≌△CEO(SAS),∴CD=CE.
24. 证明:连接OC,∵=,∴∠AOC=∠BOC.
∵CD⊥OA于D,CE⊥OB于E,
∴∠CDO=∠CEO=90°,
在△COD与△COE中,∵
∴△COD≌△COE(AAS),
∴OD=OE,
∵AO=BO,∴AD=BE
25. 解:(1)AB=CD.理由:过点O分别作OE⊥AB于点E,作OF⊥CD于点F.
∵∠APM=∠CPM,∠APM=∠BPN,∠CPM=∠DPN,
∴∠OPE=∠OPF.
∵OE⊥AB,OF⊥CD,∴∠OEP=∠OFP=90°.
又∵OP=OP,∴△OPE≌△OPF,
∴OE=OF,∴AB=CD
(2)AB=CD仍然成立.
证明:过点O分别作OE⊥AB于点E,OF⊥CD于点F.
∵OE⊥AB,OF⊥CD,∴∠OEP=∠OFP=90°.
∵∠APM=∠CPM,OP=OP,
∴△OPE≌△OPF,∴OE=OF,
∴AB=CD
