六年级下册数学教案-3.4 正反比例复习课西师大版(表格式)
文档属性
| 名称 | 六年级下册数学教案-3.4 正反比例复习课西师大版(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 10.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 00:00:00 | ||
图片预览

文档简介
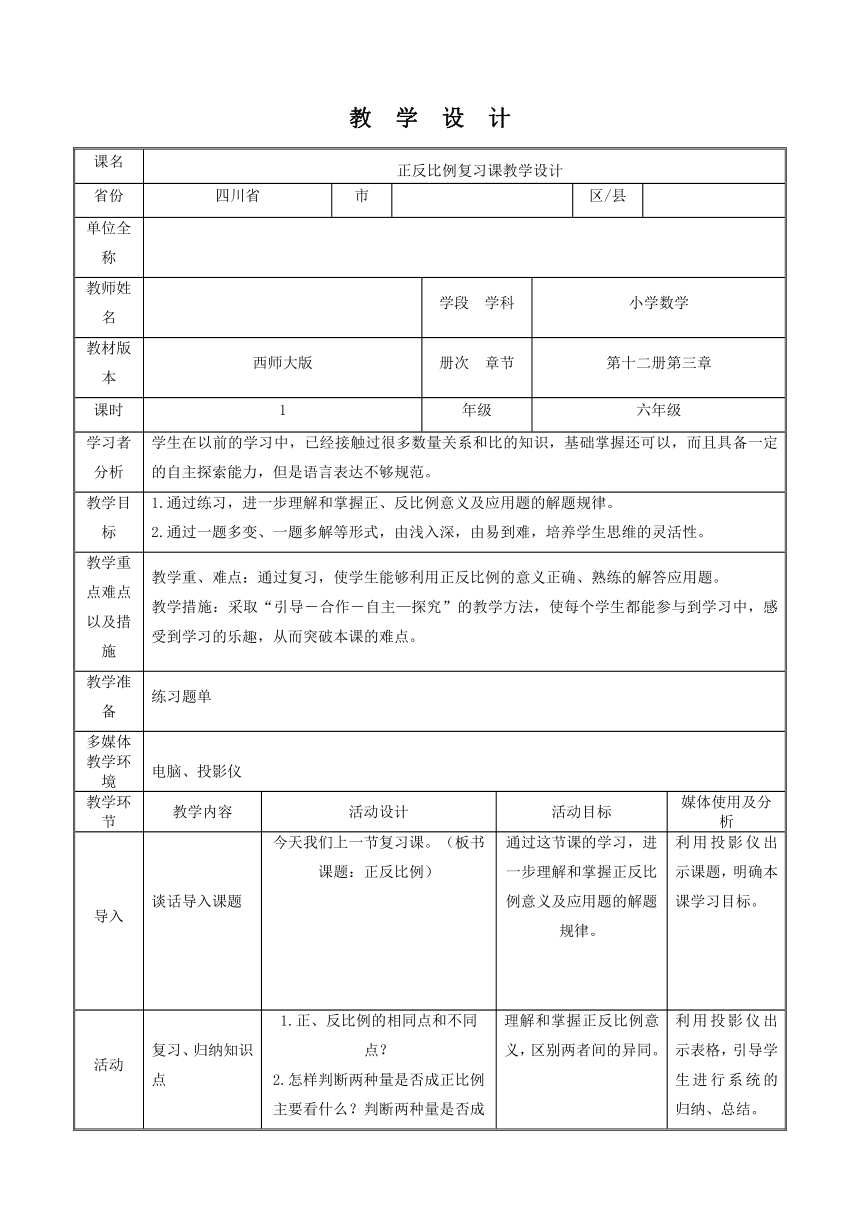
教 学 设 计
课名
正反比例复习课教学设计
省份
四川省
市
区/县
单位全称
教师姓名
学段 学科
小学数学
教材版本
西师大版
册次 章节
第十二册第三章
课时
1
年级
六年级
学习者分析
学生在以前的学习中,已经接触过很多数量关系和比的知识,基础掌握还可以,而且具备一定的自主探索能力,但是语言表达不够规范。
教学目标
1.通过练习,进一步理解和掌握正、反比例意义及应用题的解题规律。
2.通过一题多变、一题多解等形式,由浅入深,由易到难,培养学生思维的灵活性。
教学重点难点以及措施
教学重、难点:通过复习,使学生能够利用正反比例的意义正确、熟练的解答应用题。
教学措施:采取“引导-合作-自主—探究”的教学方法,使每个学生都能参与到学习中,感受到学习的乐趣,从而突破本课的难点。
教学准备
练习题单
多媒体教学环境
电脑、投影仪
教学环节
教学内容
活动设计
活动目标
媒体使用及分析
导入
谈话导入课题
今天我们上一节复习课。(板书课题:正反比例)
通过这节课的学习,进一步理解和掌握正反比例意义及应用题的解题规律。
利用投影仪出示课题,明确本课学习目标。
活动
复习、归纳知识点
1.正、反比例的相同点和不同点?
2.怎样判断两种量是否成正比例主要看什么?判断两种量是否成反比例呢?
理解和掌握正反比例意义,区别两者间的异同。
利用投影仪出示表格,引导学生进行系统的归纳、总结。
活动
判断下面每题里相关联的两种量成不成比例?如果成比例,成什么比例?
1.总价一定,单价和数量。
2.路程一定,已行的路程和剩下的路程。
3.除数一定,被除数和除数。
4.全班人数一定,出勤人数和缺勤人数。
5.全班人数一定,出勤人数和出勤率。
6.被除数一定,除数和商。
7.分数的值一定,它的分子和分母。
8.一个圆的直径和周长。
9.一根铁丝剪成同样长的段数与每段的长度。
理解掌握:
相关联的两个数的比值(商)一定,这样的两个量叫做成正比例的量;
相关联的两个数的乘积一定,这样的两个量叫做成反比例的量。
利用投影仪出示各练习题,加深学生对正反比例的理解。
活动
判断表格中a、b两个量是成什么比例的量,再根据规律完成表格。
a
12
3
1.5
b
8
0.5
3
2
a
24
7.5
6
2.5
b
5
16
15
根据已知两组数的商或乘积规律验证a和b成正比例或者反比例,然后根据比例的知识完成练习。
利用投影仪出示各练习题,提高学生对正反比例的应用。
活动
正、反比例在生活中的应用
给我们的教室铺地板砖,方砖的面积和所需块数是不是成反比例?
铺地面积一定时,方砖边长与所需块数成不成比例?为什么?
理解:
1.在教室地面面积一定的条件下,方砖的面积和所需块数成反比例;
2.方砖边长与所需块数不成反比例。
利用投影仪出示铺地砖动画,引导学生理解:方砖的面积和所需块数是两种相关联的量;方砖的面积大,所需块数少;方砖的面积小,所需块数多。
活动
比一比,想一想,每一组题中有什么不同,你会用比例知识解答吗?
(1)加工一批机器零件,4小时加工60个。照这样计算,8小时加工多少个?
(2)加工一批机器零件,每小时加工60个,要8小时完成;如果每小时加工80个,要几小时完成?
引导学生发现:较复杂的反比例应用题,其复杂性表现在两个方面。一是已知条件发生变化,引起未知数X对应值的复杂化。二是问题发生变化,引起未知数X的复杂化。但不管怎样,我们要紧扣反比例的意义,对应用题中两相关联的量进行正确的判断。
利用投影仪出示两组题型,引导学生比较理解较复杂的反比例应用题,其复杂性表现在两个方面。
拓展延伸
用正反两种比例解答
一辆汽车原计划每小时行80千米,从甲地到乙地要4.5小时。实际0.4小时行驶了36千米。照这样的速度,行完全程实际需要几小时?
引导学生获得知识经验:解答正反比例应用题,条件和问题不管多么复杂,我们要紧扣正反比例的意义,从题中的定量入手,对应用题中两种相关联的量进行正确的判断。定量等于两种相关联的量相除,则成正比例;定量等于两种相关联的量相乘,则成反比例。
全课小结
总结用正反两种比例解答问题的方法
总结用正反两种比例解答问题的方法
学生回顾本课所学。
课名
正反比例复习课教学设计
省份
四川省
市
区/县
单位全称
教师姓名
学段 学科
小学数学
教材版本
西师大版
册次 章节
第十二册第三章
课时
1
年级
六年级
学习者分析
学生在以前的学习中,已经接触过很多数量关系和比的知识,基础掌握还可以,而且具备一定的自主探索能力,但是语言表达不够规范。
教学目标
1.通过练习,进一步理解和掌握正、反比例意义及应用题的解题规律。
2.通过一题多变、一题多解等形式,由浅入深,由易到难,培养学生思维的灵活性。
教学重点难点以及措施
教学重、难点:通过复习,使学生能够利用正反比例的意义正确、熟练的解答应用题。
教学措施:采取“引导-合作-自主—探究”的教学方法,使每个学生都能参与到学习中,感受到学习的乐趣,从而突破本课的难点。
教学准备
练习题单
多媒体教学环境
电脑、投影仪
教学环节
教学内容
活动设计
活动目标
媒体使用及分析
导入
谈话导入课题
今天我们上一节复习课。(板书课题:正反比例)
通过这节课的学习,进一步理解和掌握正反比例意义及应用题的解题规律。
利用投影仪出示课题,明确本课学习目标。
活动
复习、归纳知识点
1.正、反比例的相同点和不同点?
2.怎样判断两种量是否成正比例主要看什么?判断两种量是否成反比例呢?
理解和掌握正反比例意义,区别两者间的异同。
利用投影仪出示表格,引导学生进行系统的归纳、总结。
活动
判断下面每题里相关联的两种量成不成比例?如果成比例,成什么比例?
1.总价一定,单价和数量。
2.路程一定,已行的路程和剩下的路程。
3.除数一定,被除数和除数。
4.全班人数一定,出勤人数和缺勤人数。
5.全班人数一定,出勤人数和出勤率。
6.被除数一定,除数和商。
7.分数的值一定,它的分子和分母。
8.一个圆的直径和周长。
9.一根铁丝剪成同样长的段数与每段的长度。
理解掌握:
相关联的两个数的比值(商)一定,这样的两个量叫做成正比例的量;
相关联的两个数的乘积一定,这样的两个量叫做成反比例的量。
利用投影仪出示各练习题,加深学生对正反比例的理解。
活动
判断表格中a、b两个量是成什么比例的量,再根据规律完成表格。
a
12
3
1.5
b
8
0.5
3
2
a
24
7.5
6
2.5
b
5
16
15
根据已知两组数的商或乘积规律验证a和b成正比例或者反比例,然后根据比例的知识完成练习。
利用投影仪出示各练习题,提高学生对正反比例的应用。
活动
正、反比例在生活中的应用
给我们的教室铺地板砖,方砖的面积和所需块数是不是成反比例?
铺地面积一定时,方砖边长与所需块数成不成比例?为什么?
理解:
1.在教室地面面积一定的条件下,方砖的面积和所需块数成反比例;
2.方砖边长与所需块数不成反比例。
利用投影仪出示铺地砖动画,引导学生理解:方砖的面积和所需块数是两种相关联的量;方砖的面积大,所需块数少;方砖的面积小,所需块数多。
活动
比一比,想一想,每一组题中有什么不同,你会用比例知识解答吗?
(1)加工一批机器零件,4小时加工60个。照这样计算,8小时加工多少个?
(2)加工一批机器零件,每小时加工60个,要8小时完成;如果每小时加工80个,要几小时完成?
引导学生发现:较复杂的反比例应用题,其复杂性表现在两个方面。一是已知条件发生变化,引起未知数X对应值的复杂化。二是问题发生变化,引起未知数X的复杂化。但不管怎样,我们要紧扣反比例的意义,对应用题中两相关联的量进行正确的判断。
利用投影仪出示两组题型,引导学生比较理解较复杂的反比例应用题,其复杂性表现在两个方面。
拓展延伸
用正反两种比例解答
一辆汽车原计划每小时行80千米,从甲地到乙地要4.5小时。实际0.4小时行驶了36千米。照这样的速度,行完全程实际需要几小时?
引导学生获得知识经验:解答正反比例应用题,条件和问题不管多么复杂,我们要紧扣正反比例的意义,从题中的定量入手,对应用题中两种相关联的量进行正确的判断。定量等于两种相关联的量相除,则成正比例;定量等于两种相关联的量相乘,则成反比例。
全课小结
总结用正反两种比例解答问题的方法
总结用正反两种比例解答问题的方法
学生回顾本课所学。
