2020年苏科新版九年级数学下册《第6章 图形的相似》单元测试卷(解析版)
文档属性
| 名称 | 2020年苏科新版九年级数学下册《第6章 图形的相似》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 478.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 15:29:02 | ||
图片预览

文档简介
2020年苏科新版九年级数学下册《第6章 图形的相似》单元测试卷
一.选择题(共12小题)
1.已知=,则的值为( )
A. B. C. D.
2.下列各组中的四条线段成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、5cm、6cm、7cm
C.3cm、4cm、5cm、6cm D.6cm、3cm、8cm、4cm
3.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
4.已知线段a,b,c,求作线段x,使,下列作法中正确的是( )
A. B.
C. D.
5.下列说法正确的是( )
A.相似三角形一定全等
B.不相似的三角形不一定全等
C.全等三角形不一定是相似三角形
D.全等三角形一定是相似三角形
6.如果两个相似的三角形面积之比为4:9,那么它们对应的角平分线之比为( )
A.2:3 B.4:9 C.16:81 D.9:13
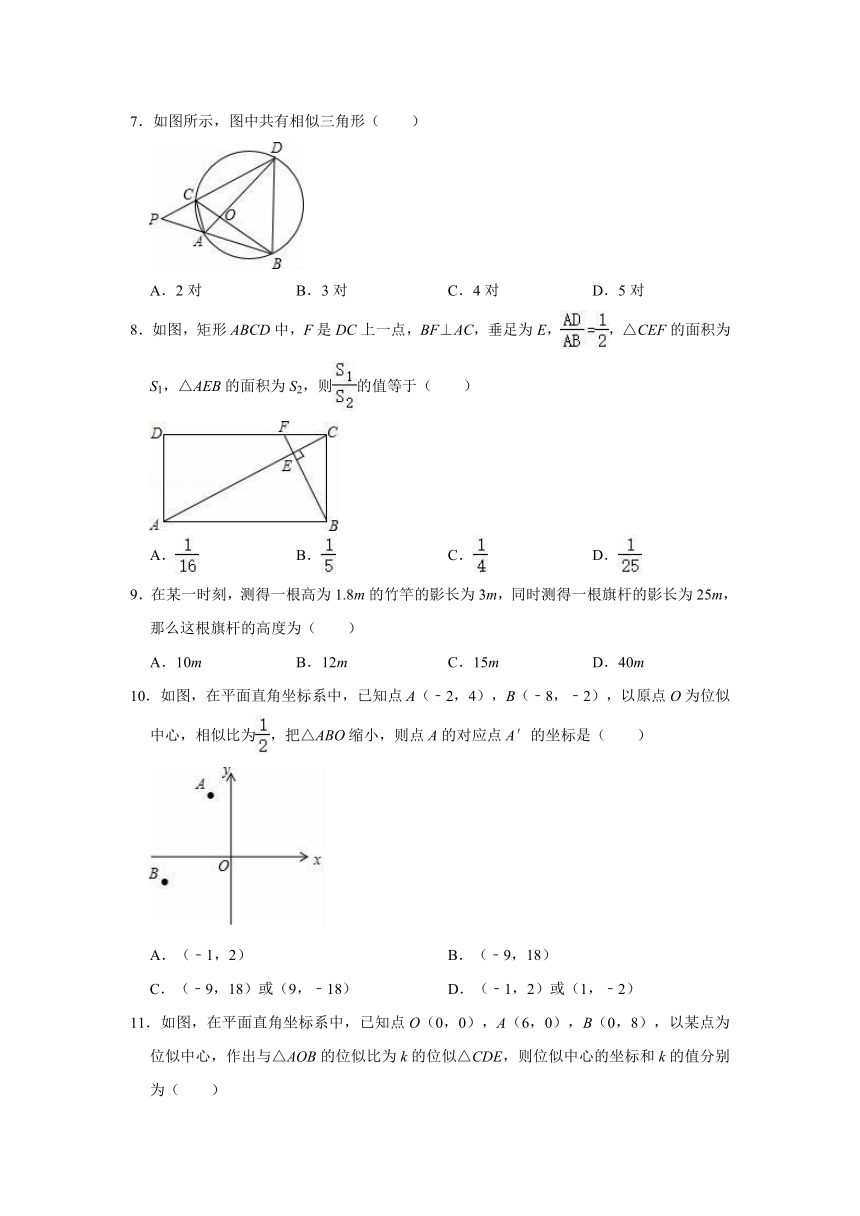
7.如图所示,图中共有相似三角形( )
A.2对 B.3对 C.4对 D.5对
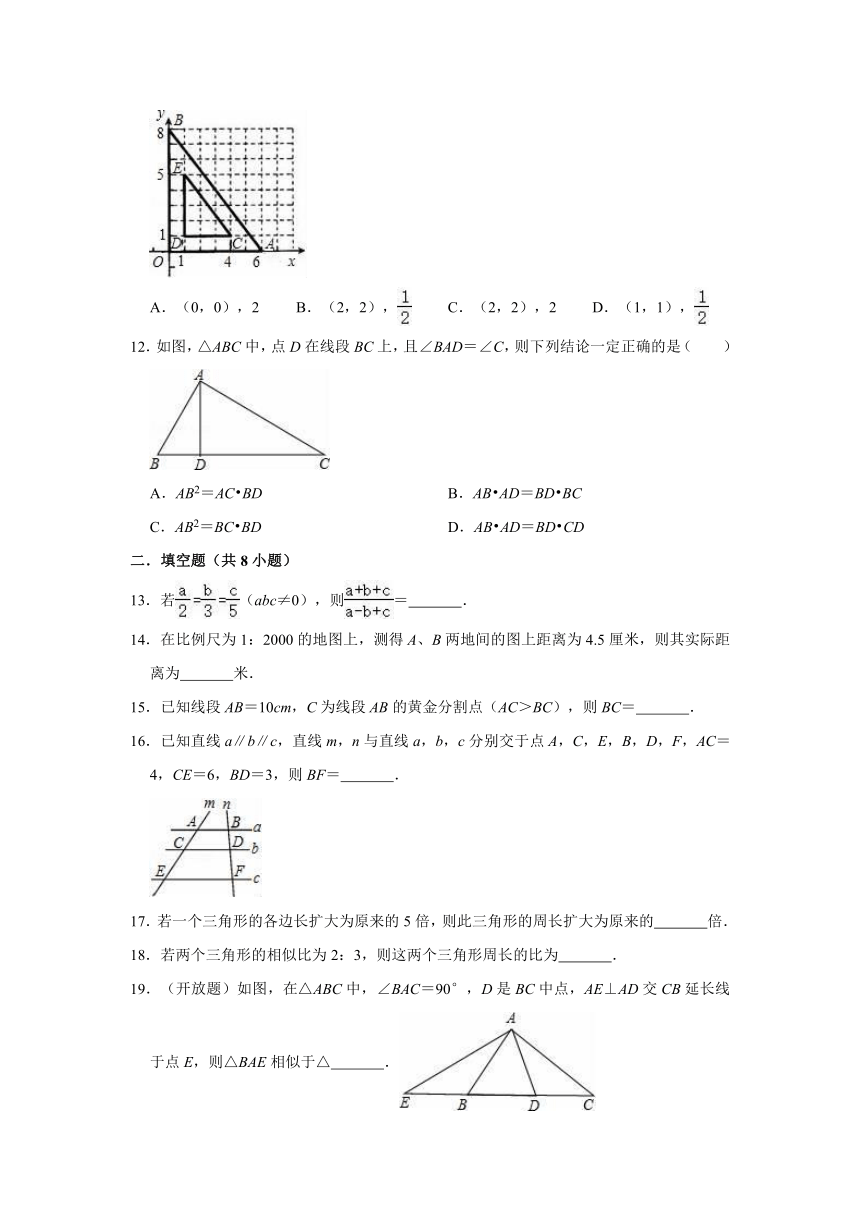
8.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,,△CEF的面积为S1,△AEB的面积为S2,则的值等于( )
A. B. C. D.
9.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.10m B.12m C.15m D.40m
10.如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
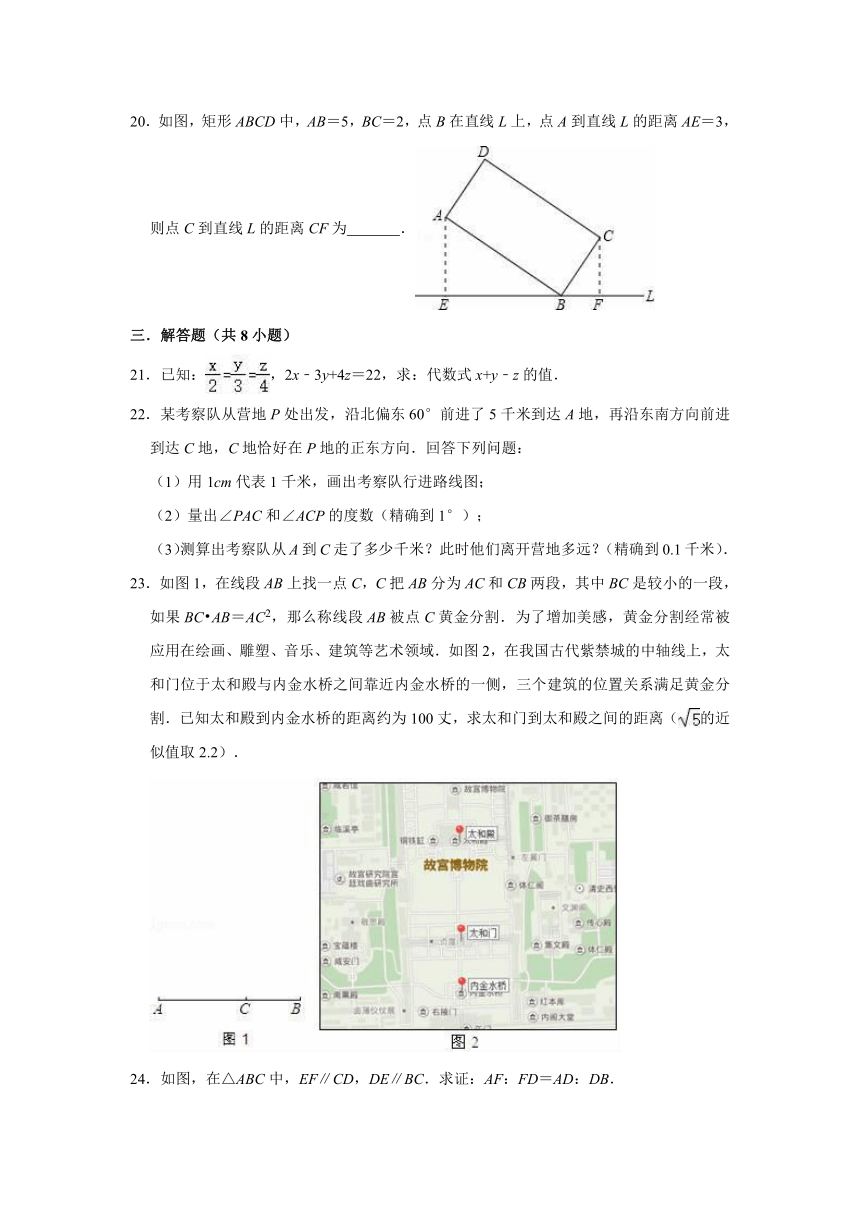
11.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(1,1),
12.如图,△ABC中,点D在线段BC上,且∠BAD=∠C,则下列结论一定正确的是( )
A.AB2=AC?BD B.AB?AD=BD?BC
C.AB2=BC?BD D.AB?AD=BD?CD
二.填空题(共8小题)
13.若(abc≠0),则= .
14.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为 米.
15.已知线段AB=10cm,C为线段AB的黄金分割点(AC>BC),则BC= .
16.已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF= .
17.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
18.若两个三角形的相似比为2:3,则这两个三角形周长的比为 .
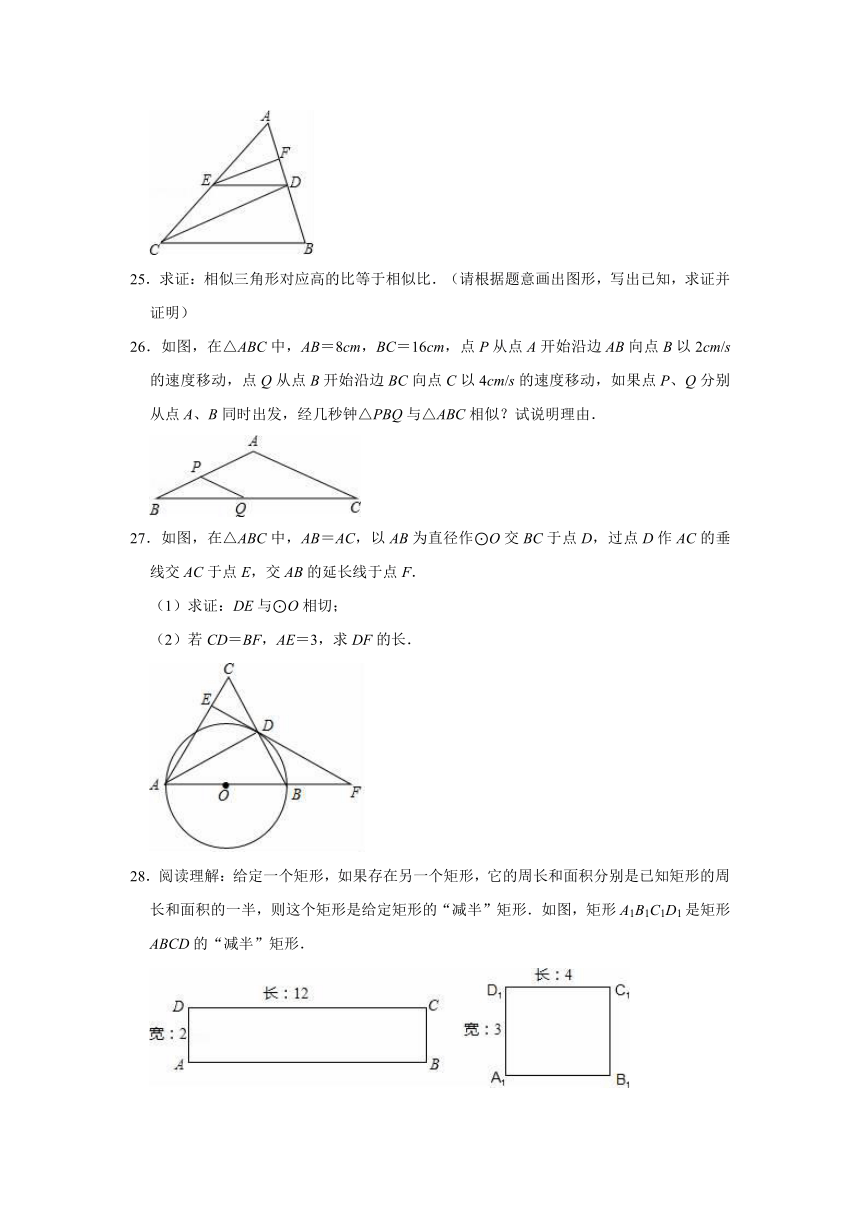
19.(开放题)如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于点E,则△BAE相似于△ .
20.如图,矩形ABCD中,AB=5,BC=2,点B在直线L上,点A到直线L的距离AE=3,则点C到直线L的距离CF为 .
三.解答题(共8小题)
21.已知:,2x﹣3y+4z=22,求:代数式x+y﹣z的值.
22.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
23.如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BC?AB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在我国古代紫禁城的中轴线上,太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,求太和门到太和殿之间的距离(的近似值取2.2).
24.如图,在△ABC中,EF∥CD,DE∥BC.求证:AF:FD=AD:DB.
25.求证:相似三角形对应高的比等于相似比.(请根据题意画出图形,写出已知,求证并证明)
26.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
27.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
28.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
2020年苏科新版九年级数学下册《第6章 图形的相似》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.已知=,则的值为( )
A. B. C. D.
【分析】设=k,则a=2k,b=5k,代入所求的式子求解即可.
【解答】解:设=k,则a=2k,b=5k.
则原式==.
故选:A.
【点评】本题考查比例的性质,正确进行设未知数是本题的关键.
2.下列各组中的四条线段成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、5cm、6cm、7cm
C.3cm、4cm、5cm、6cm D.6cm、3cm、8cm、4cm
【分析】根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案.
【解答】解:A.6×1≠2×4,故本选项错误;
B.4×7≠5×6,故本选项错误;
C.3×6≠4×5,故本选项错误;
D.6×4=3×8,故本选项正确;
故选:D.
【点评】此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
3.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
【分析】根据黄金分割的定义得到BC2=AC?AB,再利用正方形和矩形的面积公式有S1=BC2,S2=AC?AB,即可得到S1=S2.
【解答】解:∵C是线段AB的黄金分割点,且BC>AC,
∴BC2=AC?AB,
∵S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,
∴S1=BC2,S2=AC?AB,
∴S1=S2.
故选:B.
【点评】本题考查了黄金分割的定义:一个点把一条线段分成较长线段和较短线段,并且较长线段是较短线段和整个线段的比例中项,那么就说这个点把这条线段黄金分割,这个点叫这条线段的黄金分割点.
4.已知线段a,b,c,求作线段x,使,下列作法中正确的是( )
A. B.
C. D.
【分析】根据平行线的性质一一分析.
【解答】解:A、根据平行线的性质得,故x=,故此选项错误;
B、根据平行线的性质得,故x=,故此选项错误;
C、根据平行线的性质得,故x=,故此选项错误;
D、根据平行线的性质得故x=,故此选项正确.
故选:D.
【点评】本题主要考查了利用平行线的性质画图的方法.
5.下列说法正确的是( )
A.相似三角形一定全等
B.不相似的三角形不一定全等
C.全等三角形不一定是相似三角形
D.全等三角形一定是相似三角形
【分析】根据全等三角形是相似三角形的特殊情况,对各选项分析判断后利用排除法求解.
【解答】解:A、相似三角形大小不一定相等,所以不一定全等,故本选项错误;
B、不相似的三角形一定不全等,不是不一定全等,故本选项错误;
C、全等三角形一定是相似三角形,故本选项错误;
D、全等三角形是相似比为1的相似三角形,所以一定是相似三角形,正确.
故选:D.
【点评】本题考查了全等三角形与相似三角形的关系,熟记全等三角形是相似三角形的特殊情况是解题的关键.
6.如果两个相似的三角形面积之比为4:9,那么它们对应的角平分线之比为( )
A.2:3 B.4:9 C.16:81 D.9:13
【分析】如果两个相似的三角形面积之比为4:9,根据相似三角形的性质,则相似比是2:3,相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比,所以它们对应的角平分线之比为2:3.
【解答】解:两个相似的三角形面积之比为4:9,故它们的相似比为2:3,所以它们对应的角平分线之比为2:3.故选A.
【点评】相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
7.如图所示,图中共有相似三角形( )
A.2对 B.3对 C.4对 D.5对
【分析】可以运用相似三角形的判定方法进行验证.
【解答】解:共四对,分别是△PAC∽△PBD、△AOC∽△DOB、
△AOB∽△COD、△PAD∽△PCB.
故选:C.
【点评】主要考查相似三角形的判定方法的掌握情况.
8.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,,△CEF的面积为S1,△AEB的面积为S2,则的值等于( )
A. B. C. D.
【分析】根据已知条件设AD=BC=a,则AB=CD=2a,由勾股定理得到AC=a,根据相似三角形的性质得到BC2=CE?CA,AB2=AE?AC求得CE=,AE=,得到=,根据相似三角形的性质即可得到结论.
【解答】解:∵,
∴设AD=BC=a,则AB=CD=2a,
∴AC=a,
∵BF⊥AC,
∴△CBE∽△CAB,△AEB∽△ABC,
∴BC2=CE?CA,AB2=AE?AC
∴a2=CE?a,4a2=AE?a,
∴CE=,AE=,
∴=,
∵△CEF∽△AEB,
∴=()2=,
故选:A.
【点评】本题考查了矩形的性质及相似三角形的判定,能够牢记射影定理的内容对解决本题起到至关重要的作用,难度不大.
9.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.10m B.12m C.15m D.40m
【分析】根据同时同地物高与影长成正比列式计算即可得解.
【解答】解:设旗杆高度为x米,
由题意得,=,
解得:x=15.
故选:C.
【点评】本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比,需熟记.
10.如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
【分析】根据位似变换的性质计算即可.
【解答】解:点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,相似比为,把△ABO缩小,
则点A的对应点A′的坐标是(﹣2×,4×)或(﹣2×(﹣),4×(﹣)),即(﹣1,2)或(1,﹣2),
故选:D.
【点评】本题考查的是位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
11.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(1,1),
【分析】直接利用位似图形的性质分别得出位似中心和位似比.
【解答】解:如图所示:位似中心F的坐标为:(2,2),
k的值为:=.
故选:B.
【点评】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
12.如图,△ABC中,点D在线段BC上,且∠BAD=∠C,则下列结论一定正确的是( )
A.AB2=AC?BD B.AB?AD=BD?BC
C.AB2=BC?BD D.AB?AD=BD?CD
【分析】先证明△BAD∽△BCA,则利用相似的性质得AB:BC=BD:AB,然后根据比例性质得到AB2=BC?BD.
【解答】解:∵∠BAD=∠C,
而∠ABD=∠CBA,
∴△BAD∽△BCA,
∴AB:BC=BD:AB,
∴AB2=BC?BD.
故选:C.
【点评】本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.也考查了相似三角形的判定与性质.
二.填空题(共8小题)
13.若(abc≠0),则= .
【分析】先设=k,可得a=2k,b=3k,c=5k,再把a、b、c的值都代入所求式子计算即可.
【解答】解:设=k,那么a=2k,b=3k,c=5k,
∴==.
故答案是:.
【点评】本题考查了比例的性质.解题的关键是先假设=k,得出a=2k,b=3k,c=5k,降低计算难度.
14.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为 90 米.
【分析】根据比例尺=图上距离:实际距离,依题意列出比例式,即可求得实际距离.
【解答】解:设A,B两地的实际距离为xcm,则:
1:2000=4.5:x,
解得x=9000.
9000cm=90m.
故答案为:90.
【点评】本题考查了比例尺的定义.要求能够根据比例尺由图上距离正确计算实际距离,注意单位的换算.
15.已知线段AB=10cm,C为线段AB的黄金分割点(AC>BC),则BC= (15﹣5)cm .
【分析】根据黄金分割的定义得到AC=AB=AC=5﹣5,然后计算AB﹣AC即可得到BC.
【解答】解:∵C为线段AB的黄金分割点(AC>BC),
∴AC=AB=AC=×10=5﹣5,
∴BC=AB﹣AC=10﹣(5﹣5)=(15﹣5)cm.
故答案为(15﹣5)cm.
【点评】本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=AB≈0.618AB,并且线段AB的黄金分割点有两个.
16.已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF= 7.5 .
【分析】根据平行线分线段成比例定理得到比例式,求出DF,结合图形计算即可.
【解答】解:∵a∥b∥c,
∴=,即=,
解得DF=4.5,
∴BF=BD+DF=3+4.5=7.5,
故答案为:7.5.
【点评】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
17.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 5 倍.
【分析】由题意一个三角形的各边长扩大为原来的5倍,根据相似三角形的性质及对应边长成比例来求解.
【解答】解:∵一个三角形的各边长扩大为原来的5倍,
∴扩大后的三角形与原三角形相似,
∵相似三角形的周长的比等于相似比,
∴这个三角形的周长扩大为原来的5倍,
故答案为:5.
【点评】本题考查了相似三角形的性质:相似三角形的周长的比等于相似比.
18.若两个三角形的相似比为2:3,则这两个三角形周长的比为 2:3 .
【分析】根据相似三角形的性质:周长比等于相似比即可解得.
【解答】解:∵两个相似三角形的相似比为 2:3,
∴它们的周长比为:2:3.
故答案为:2:3.
【点评】此题主要考查相似三角形的性质:相似三角形的周长比等于相似比.
19.(开放题)如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于点E,则△BAE相似于△ ACE .
【分析】根据两组对应角相等的两三角形相似即可解答.
【解答】解:因为在△ABC中,∠BAC=90°,D是BC中点,所以AD=DC,即∠C=∠DAC.
又因为AE⊥AD,所以∠EAB=∠DAC=∠C,
因为∠E是公共角,所以△BAE∽△ACE.
【点评】此题主要考查学生对有两组角对应相等的两个三角形相似的运用.
20.如图,矩形ABCD中,AB=5,BC=2,点B在直线L上,点A到直线L的距离AE=3,则点C到直线L的距离CF为 1.6 .
【分析】易得△AEB和△BFC相似,那么利用相似三角形的对应边成比例可得BF长,进而利用勾股定理可得CF长.
【解答】解:由题意得:∠AEB=∠CFB=90°,
∴∠EAB+∠ABE=90°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
∴△AEB∽△BFC,
∴AE:BF=AB:BC,
∵AB=5,BC=2,AE=3,
∴BF=1.2,
∴CF=1.6.
【点评】用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例及勾股定理等知识.
三.解答题(共8小题)
21.已知:,2x﹣3y+4z=22,求:代数式x+y﹣z的值.
【分析】根据题意,设x=2k,y=3k,z=4k.又因为2x﹣3y+4z=22,则可得k的值,从而求得x、y、z的值,故x+y+z可求.
【解答】解:设,
则x=2k,y=3k,z=4k,
∵2x﹣3y+4z=22,
∴4k﹣9k+16k=22,
∴k=2,
∴x+y﹣z=2k+3k﹣4k=k=2.
【点评】本题考查了比例的性质和代数式求值.已知几个量的比值时,常用的解法是:设一个未知数,把题目中的几个量用所设的未知数表示出来,实现消元.
22.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
【分析】(1)先画出方向标,再确定方位角、比例尺作图;
(2)动手操作利用量角器测量即可;
(3)先利用刻度尺测量出图上距离,再根据比例尺换算成实际距离.
【解答】解:(1)路线图(6分)(P、A、C点各2分)
注意:起点是必须在所给的图形中画,否则即使画图正确扣;(2分)
(2)量得∠PAC≈105°,∠ACP≈45°;(9分)(只有1个正确得2分)
(3)量路线图得AC≈3.5厘米,PC≈6.8厘米.
∴AC≈3.5千米;PC≈6.8千米(13分)
【点评】主要考查了方位角的作图能力.要会根据比例尺准确的作图,并根据图例测算出实际距离.
23.如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BC?AB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在我国古代紫禁城的中轴线上,太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,求太和门到太和殿之间的距离(的近似值取2.2).
【分析】根据黄金分割的概念列出比例式,计算即可.
【解答】解:设太和门到太和殿的距离为x丈,
由题意可得,x2=100(100﹣x)
解得,,(舍去)
则x≈﹣50+50×2.2=60,
答:太和门到太和殿的距离为60丈.
【点评】本题开车的是黄金分割的概念和性质,把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,叫做把线段AB黄金分割.
24.如图,在△ABC中,EF∥CD,DE∥BC.求证:AF:FD=AD:DB.
【分析】根据平行线分线段成比例定理得出=,=,推出=即可.
【解答】解:∵EF∥CD,DE∥BC,
∴=,=,
∴=,
即AF:FD=AD:DB.
【点评】本题考查了平行线分线段成比例定理的应用,注意对应成比例.
25.求证:相似三角形对应高的比等于相似比.(请根据题意画出图形,写出已知,求证并证明)
【分析】先根据题意画出图形,写出已知,求证,再证明即可.
【解答】已知:△ABC∽△A′B′C′,相似比为k,AD是△ABC的高,A′D′是△A″B″C″的高,
求证:=k,
证明:
∵△ABC∽△A′B′C′,
∴∠B=∠B′,
∵AD是△ABC的高,A′D′是△A″B″C″的高,
∴∠ADB=∠A′D′B′=90°,
∴△ABD∽△A′B′D′,
∴==k.
【点评】本题考查了相似三角形的性质和判定,能熟练地运用定理进行推理是解此题的关键.
26.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
【分析】首先设经x秒钟△PBQ与△ABC相似,由题意可得AP=2xcm,BQ=4xcm,BP=AB﹣AP=(8﹣2x)cm,又由∠B是公共角,分别从=与=分析,即可求得答案.
【解答】解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB﹣AP=(8﹣2x)cm,
∵∠B是公共角,
∵①当=,即=时,△PBQ∽△ABC,
解得:x=2;
②当=,即=时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
【点评】此题考查了相似三角形的判定.此题难度适中,属于动点型题目,注意掌握数形结合思想、分类讨论思想与方程思想的应用.
27.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
【分析】(1)连接OD,求出AC∥OD,求出OD⊥DE,根据切线的判定得出即可;
(2)求出∠1=∠2=∠F=30°,求出AD=DF,解直角三角形求出AD,即可求出答案.
【解答】(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵AB=AC,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠ADO,
∴∠1=∠ADO,
∴OD∥AC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∴OD⊥ED,
∵OD过0,
∴DE与⊙O相切;
(2)解:∵AB=AC,AD⊥BC,
∴∠1=∠2,CD=BD,
∵CD=BF,
∴BF=BD,
∴∠3=∠F,
∴∠4=∠3+∠F=2∠3,
∵OB=OD,
∴∠ODB=∠4=2∠3,
∵∠ODF=90°,
∴∠3=∠F=30°,∠4=∠ODB=60°,
∵∠ADB=90°,
∴∠2=∠1=30°,
∴∠2=∠F,
∴DF=AD,
∵∠1=30°,∠AED=90°,
∴AD=2ED,
∵AE2+DE2=AD2,AE=3,
∴AD=2,
∴DF=2.
【点评】本题考查了等腰三角形的性质,三角形的外角性质,圆周角定理,切线的判定定理,解直角三角形等知识点,能综合运用定理进行推理是解此题的关键.
28.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
【分析】(1)假设存在,不妨设“减半”矩形的长和宽分别为x、y,根据如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,可列出方程组求解.
(2)正方形和其他的正方形是相似图形,周长比是2,面积比就应该是4,所以不存在“减半”正方形.
【解答】解:(1)不存在.(1分)
假设存在,不妨设“减半”矩形的长和宽分别为x、y,
则,(3分)
由①得:y=﹣x③,
把③代入②得:x2﹣x+1=0,
b2﹣4ac=﹣4<0,(5分)
所以不存在;
(2)不存在.(6分)
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.(10分)
【点评】本题考查反证法和相似图形的性质,关键知道相似图形的面积比,周长比的关系.
一.选择题(共12小题)
1.已知=,则的值为( )
A. B. C. D.
2.下列各组中的四条线段成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、5cm、6cm、7cm
C.3cm、4cm、5cm、6cm D.6cm、3cm、8cm、4cm
3.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
4.已知线段a,b,c,求作线段x,使,下列作法中正确的是( )
A. B.
C. D.
5.下列说法正确的是( )
A.相似三角形一定全等
B.不相似的三角形不一定全等
C.全等三角形不一定是相似三角形
D.全等三角形一定是相似三角形
6.如果两个相似的三角形面积之比为4:9,那么它们对应的角平分线之比为( )
A.2:3 B.4:9 C.16:81 D.9:13
7.如图所示,图中共有相似三角形( )
A.2对 B.3对 C.4对 D.5对
8.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,,△CEF的面积为S1,△AEB的面积为S2,则的值等于( )
A. B. C. D.
9.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.10m B.12m C.15m D.40m
10.如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
11.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(1,1),
12.如图,△ABC中,点D在线段BC上,且∠BAD=∠C,则下列结论一定正确的是( )
A.AB2=AC?BD B.AB?AD=BD?BC
C.AB2=BC?BD D.AB?AD=BD?CD
二.填空题(共8小题)
13.若(abc≠0),则= .
14.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为 米.
15.已知线段AB=10cm,C为线段AB的黄金分割点(AC>BC),则BC= .
16.已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF= .
17.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
18.若两个三角形的相似比为2:3,则这两个三角形周长的比为 .
19.(开放题)如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于点E,则△BAE相似于△ .
20.如图,矩形ABCD中,AB=5,BC=2,点B在直线L上,点A到直线L的距离AE=3,则点C到直线L的距离CF为 .
三.解答题(共8小题)
21.已知:,2x﹣3y+4z=22,求:代数式x+y﹣z的值.
22.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
23.如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BC?AB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在我国古代紫禁城的中轴线上,太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,求太和门到太和殿之间的距离(的近似值取2.2).
24.如图,在△ABC中,EF∥CD,DE∥BC.求证:AF:FD=AD:DB.
25.求证:相似三角形对应高的比等于相似比.(请根据题意画出图形,写出已知,求证并证明)
26.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
27.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
28.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
2020年苏科新版九年级数学下册《第6章 图形的相似》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.已知=,则的值为( )
A. B. C. D.
【分析】设=k,则a=2k,b=5k,代入所求的式子求解即可.
【解答】解:设=k,则a=2k,b=5k.
则原式==.
故选:A.
【点评】本题考查比例的性质,正确进行设未知数是本题的关键.
2.下列各组中的四条线段成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、5cm、6cm、7cm
C.3cm、4cm、5cm、6cm D.6cm、3cm、8cm、4cm
【分析】根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案.
【解答】解:A.6×1≠2×4,故本选项错误;
B.4×7≠5×6,故本选项错误;
C.3×6≠4×5,故本选项错误;
D.6×4=3×8,故本选项正确;
故选:D.
【点评】此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
3.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
【分析】根据黄金分割的定义得到BC2=AC?AB,再利用正方形和矩形的面积公式有S1=BC2,S2=AC?AB,即可得到S1=S2.
【解答】解:∵C是线段AB的黄金分割点,且BC>AC,
∴BC2=AC?AB,
∵S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,
∴S1=BC2,S2=AC?AB,
∴S1=S2.
故选:B.
【点评】本题考查了黄金分割的定义:一个点把一条线段分成较长线段和较短线段,并且较长线段是较短线段和整个线段的比例中项,那么就说这个点把这条线段黄金分割,这个点叫这条线段的黄金分割点.
4.已知线段a,b,c,求作线段x,使,下列作法中正确的是( )
A. B.
C. D.
【分析】根据平行线的性质一一分析.
【解答】解:A、根据平行线的性质得,故x=,故此选项错误;
B、根据平行线的性质得,故x=,故此选项错误;
C、根据平行线的性质得,故x=,故此选项错误;
D、根据平行线的性质得故x=,故此选项正确.
故选:D.
【点评】本题主要考查了利用平行线的性质画图的方法.
5.下列说法正确的是( )
A.相似三角形一定全等
B.不相似的三角形不一定全等
C.全等三角形不一定是相似三角形
D.全等三角形一定是相似三角形
【分析】根据全等三角形是相似三角形的特殊情况,对各选项分析判断后利用排除法求解.
【解答】解:A、相似三角形大小不一定相等,所以不一定全等,故本选项错误;
B、不相似的三角形一定不全等,不是不一定全等,故本选项错误;
C、全等三角形一定是相似三角形,故本选项错误;
D、全等三角形是相似比为1的相似三角形,所以一定是相似三角形,正确.
故选:D.
【点评】本题考查了全等三角形与相似三角形的关系,熟记全等三角形是相似三角形的特殊情况是解题的关键.
6.如果两个相似的三角形面积之比为4:9,那么它们对应的角平分线之比为( )
A.2:3 B.4:9 C.16:81 D.9:13
【分析】如果两个相似的三角形面积之比为4:9,根据相似三角形的性质,则相似比是2:3,相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比,所以它们对应的角平分线之比为2:3.
【解答】解:两个相似的三角形面积之比为4:9,故它们的相似比为2:3,所以它们对应的角平分线之比为2:3.故选A.
【点评】相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
7.如图所示,图中共有相似三角形( )
A.2对 B.3对 C.4对 D.5对
【分析】可以运用相似三角形的判定方法进行验证.
【解答】解:共四对,分别是△PAC∽△PBD、△AOC∽△DOB、
△AOB∽△COD、△PAD∽△PCB.
故选:C.
【点评】主要考查相似三角形的判定方法的掌握情况.
8.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,,△CEF的面积为S1,△AEB的面积为S2,则的值等于( )
A. B. C. D.
【分析】根据已知条件设AD=BC=a,则AB=CD=2a,由勾股定理得到AC=a,根据相似三角形的性质得到BC2=CE?CA,AB2=AE?AC求得CE=,AE=,得到=,根据相似三角形的性质即可得到结论.
【解答】解:∵,
∴设AD=BC=a,则AB=CD=2a,
∴AC=a,
∵BF⊥AC,
∴△CBE∽△CAB,△AEB∽△ABC,
∴BC2=CE?CA,AB2=AE?AC
∴a2=CE?a,4a2=AE?a,
∴CE=,AE=,
∴=,
∵△CEF∽△AEB,
∴=()2=,
故选:A.
【点评】本题考查了矩形的性质及相似三角形的判定,能够牢记射影定理的内容对解决本题起到至关重要的作用,难度不大.
9.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )
A.10m B.12m C.15m D.40m
【分析】根据同时同地物高与影长成正比列式计算即可得解.
【解答】解:设旗杆高度为x米,
由题意得,=,
解得:x=15.
故选:C.
【点评】本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比,需熟记.
10.如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
【分析】根据位似变换的性质计算即可.
【解答】解:点A(﹣2,4),B(﹣8,﹣2),以原点O为位似中心,相似比为,把△ABO缩小,
则点A的对应点A′的坐标是(﹣2×,4×)或(﹣2×(﹣),4×(﹣)),即(﹣1,2)或(1,﹣2),
故选:D.
【点评】本题考查的是位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
11.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(1,1),
【分析】直接利用位似图形的性质分别得出位似中心和位似比.
【解答】解:如图所示:位似中心F的坐标为:(2,2),
k的值为:=.
故选:B.
【点评】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
12.如图,△ABC中,点D在线段BC上,且∠BAD=∠C,则下列结论一定正确的是( )
A.AB2=AC?BD B.AB?AD=BD?BC
C.AB2=BC?BD D.AB?AD=BD?CD
【分析】先证明△BAD∽△BCA,则利用相似的性质得AB:BC=BD:AB,然后根据比例性质得到AB2=BC?BD.
【解答】解:∵∠BAD=∠C,
而∠ABD=∠CBA,
∴△BAD∽△BCA,
∴AB:BC=BD:AB,
∴AB2=BC?BD.
故选:C.
【点评】本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.也考查了相似三角形的判定与性质.
二.填空题(共8小题)
13.若(abc≠0),则= .
【分析】先设=k,可得a=2k,b=3k,c=5k,再把a、b、c的值都代入所求式子计算即可.
【解答】解:设=k,那么a=2k,b=3k,c=5k,
∴==.
故答案是:.
【点评】本题考查了比例的性质.解题的关键是先假设=k,得出a=2k,b=3k,c=5k,降低计算难度.
14.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为 90 米.
【分析】根据比例尺=图上距离:实际距离,依题意列出比例式,即可求得实际距离.
【解答】解:设A,B两地的实际距离为xcm,则:
1:2000=4.5:x,
解得x=9000.
9000cm=90m.
故答案为:90.
【点评】本题考查了比例尺的定义.要求能够根据比例尺由图上距离正确计算实际距离,注意单位的换算.
15.已知线段AB=10cm,C为线段AB的黄金分割点(AC>BC),则BC= (15﹣5)cm .
【分析】根据黄金分割的定义得到AC=AB=AC=5﹣5,然后计算AB﹣AC即可得到BC.
【解答】解:∵C为线段AB的黄金分割点(AC>BC),
∴AC=AB=AC=×10=5﹣5,
∴BC=AB﹣AC=10﹣(5﹣5)=(15﹣5)cm.
故答案为(15﹣5)cm.
【点评】本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=AB≈0.618AB,并且线段AB的黄金分割点有两个.
16.已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF= 7.5 .
【分析】根据平行线分线段成比例定理得到比例式,求出DF,结合图形计算即可.
【解答】解:∵a∥b∥c,
∴=,即=,
解得DF=4.5,
∴BF=BD+DF=3+4.5=7.5,
故答案为:7.5.
【点评】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
17.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 5 倍.
【分析】由题意一个三角形的各边长扩大为原来的5倍,根据相似三角形的性质及对应边长成比例来求解.
【解答】解:∵一个三角形的各边长扩大为原来的5倍,
∴扩大后的三角形与原三角形相似,
∵相似三角形的周长的比等于相似比,
∴这个三角形的周长扩大为原来的5倍,
故答案为:5.
【点评】本题考查了相似三角形的性质:相似三角形的周长的比等于相似比.
18.若两个三角形的相似比为2:3,则这两个三角形周长的比为 2:3 .
【分析】根据相似三角形的性质:周长比等于相似比即可解得.
【解答】解:∵两个相似三角形的相似比为 2:3,
∴它们的周长比为:2:3.
故答案为:2:3.
【点评】此题主要考查相似三角形的性质:相似三角形的周长比等于相似比.
19.(开放题)如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于点E,则△BAE相似于△ ACE .
【分析】根据两组对应角相等的两三角形相似即可解答.
【解答】解:因为在△ABC中,∠BAC=90°,D是BC中点,所以AD=DC,即∠C=∠DAC.
又因为AE⊥AD,所以∠EAB=∠DAC=∠C,
因为∠E是公共角,所以△BAE∽△ACE.
【点评】此题主要考查学生对有两组角对应相等的两个三角形相似的运用.
20.如图,矩形ABCD中,AB=5,BC=2,点B在直线L上,点A到直线L的距离AE=3,则点C到直线L的距离CF为 1.6 .
【分析】易得△AEB和△BFC相似,那么利用相似三角形的对应边成比例可得BF长,进而利用勾股定理可得CF长.
【解答】解:由题意得:∠AEB=∠CFB=90°,
∴∠EAB+∠ABE=90°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
∴△AEB∽△BFC,
∴AE:BF=AB:BC,
∵AB=5,BC=2,AE=3,
∴BF=1.2,
∴CF=1.6.
【点评】用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例及勾股定理等知识.
三.解答题(共8小题)
21.已知:,2x﹣3y+4z=22,求:代数式x+y﹣z的值.
【分析】根据题意,设x=2k,y=3k,z=4k.又因为2x﹣3y+4z=22,则可得k的值,从而求得x、y、z的值,故x+y+z可求.
【解答】解:设,
则x=2k,y=3k,z=4k,
∵2x﹣3y+4z=22,
∴4k﹣9k+16k=22,
∴k=2,
∴x+y﹣z=2k+3k﹣4k=k=2.
【点评】本题考查了比例的性质和代数式求值.已知几个量的比值时,常用的解法是:设一个未知数,把题目中的几个量用所设的未知数表示出来,实现消元.
22.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
【分析】(1)先画出方向标,再确定方位角、比例尺作图;
(2)动手操作利用量角器测量即可;
(3)先利用刻度尺测量出图上距离,再根据比例尺换算成实际距离.
【解答】解:(1)路线图(6分)(P、A、C点各2分)
注意:起点是必须在所给的图形中画,否则即使画图正确扣;(2分)
(2)量得∠PAC≈105°,∠ACP≈45°;(9分)(只有1个正确得2分)
(3)量路线图得AC≈3.5厘米,PC≈6.8厘米.
∴AC≈3.5千米;PC≈6.8千米(13分)
【点评】主要考查了方位角的作图能力.要会根据比例尺准确的作图,并根据图例测算出实际距离.
23.如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BC?AB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在我国古代紫禁城的中轴线上,太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,求太和门到太和殿之间的距离(的近似值取2.2).
【分析】根据黄金分割的概念列出比例式,计算即可.
【解答】解:设太和门到太和殿的距离为x丈,
由题意可得,x2=100(100﹣x)
解得,,(舍去)
则x≈﹣50+50×2.2=60,
答:太和门到太和殿的距离为60丈.
【点评】本题开车的是黄金分割的概念和性质,把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,叫做把线段AB黄金分割.
24.如图,在△ABC中,EF∥CD,DE∥BC.求证:AF:FD=AD:DB.
【分析】根据平行线分线段成比例定理得出=,=,推出=即可.
【解答】解:∵EF∥CD,DE∥BC,
∴=,=,
∴=,
即AF:FD=AD:DB.
【点评】本题考查了平行线分线段成比例定理的应用,注意对应成比例.
25.求证:相似三角形对应高的比等于相似比.(请根据题意画出图形,写出已知,求证并证明)
【分析】先根据题意画出图形,写出已知,求证,再证明即可.
【解答】已知:△ABC∽△A′B′C′,相似比为k,AD是△ABC的高,A′D′是△A″B″C″的高,
求证:=k,
证明:
∵△ABC∽△A′B′C′,
∴∠B=∠B′,
∵AD是△ABC的高,A′D′是△A″B″C″的高,
∴∠ADB=∠A′D′B′=90°,
∴△ABD∽△A′B′D′,
∴==k.
【点评】本题考查了相似三角形的性质和判定,能熟练地运用定理进行推理是解此题的关键.
26.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
【分析】首先设经x秒钟△PBQ与△ABC相似,由题意可得AP=2xcm,BQ=4xcm,BP=AB﹣AP=(8﹣2x)cm,又由∠B是公共角,分别从=与=分析,即可求得答案.
【解答】解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB﹣AP=(8﹣2x)cm,
∵∠B是公共角,
∵①当=,即=时,△PBQ∽△ABC,
解得:x=2;
②当=,即=时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
【点评】此题考查了相似三角形的判定.此题难度适中,属于动点型题目,注意掌握数形结合思想、分类讨论思想与方程思想的应用.
27.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.
(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
【分析】(1)连接OD,求出AC∥OD,求出OD⊥DE,根据切线的判定得出即可;
(2)求出∠1=∠2=∠F=30°,求出AD=DF,解直角三角形求出AD,即可求出答案.
【解答】(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵AB=AC,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠ADO,
∴∠1=∠ADO,
∴OD∥AC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∴OD⊥ED,
∵OD过0,
∴DE与⊙O相切;
(2)解:∵AB=AC,AD⊥BC,
∴∠1=∠2,CD=BD,
∵CD=BF,
∴BF=BD,
∴∠3=∠F,
∴∠4=∠3+∠F=2∠3,
∵OB=OD,
∴∠ODB=∠4=2∠3,
∵∠ODF=90°,
∴∠3=∠F=30°,∠4=∠ODB=60°,
∵∠ADB=90°,
∴∠2=∠1=30°,
∴∠2=∠F,
∴DF=AD,
∵∠1=30°,∠AED=90°,
∴AD=2ED,
∵AE2+DE2=AD2,AE=3,
∴AD=2,
∴DF=2.
【点评】本题考查了等腰三角形的性质,三角形的外角性质,圆周角定理,切线的判定定理,解直角三角形等知识点,能综合运用定理进行推理是解此题的关键.
28.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
【分析】(1)假设存在,不妨设“减半”矩形的长和宽分别为x、y,根据如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,可列出方程组求解.
(2)正方形和其他的正方形是相似图形,周长比是2,面积比就应该是4,所以不存在“减半”正方形.
【解答】解:(1)不存在.(1分)
假设存在,不妨设“减半”矩形的长和宽分别为x、y,
则,(3分)
由①得:y=﹣x③,
把③代入②得:x2﹣x+1=0,
b2﹣4ac=﹣4<0,(5分)
所以不存在;
(2)不存在.(6分)
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.(10分)
【点评】本题考查反证法和相似图形的性质,关键知道相似图形的面积比,周长比的关系.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
