北师大版七年级数学下册:2.3 平行线的性质 课件 (共15张PPT)
文档属性
| 名称 | 北师大版七年级数学下册:2.3 平行线的性质 课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 322.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-05 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
2.3 平行线的性质
创设情景 明确目标
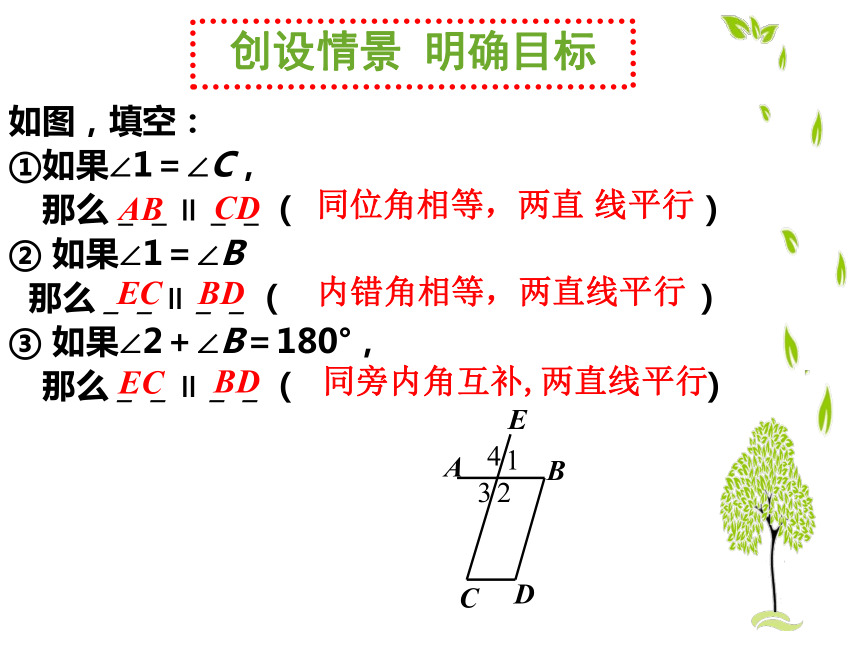
如图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( )
AB
CD
EC
BD
同位角相等,两直 线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
创设情景 明确目标
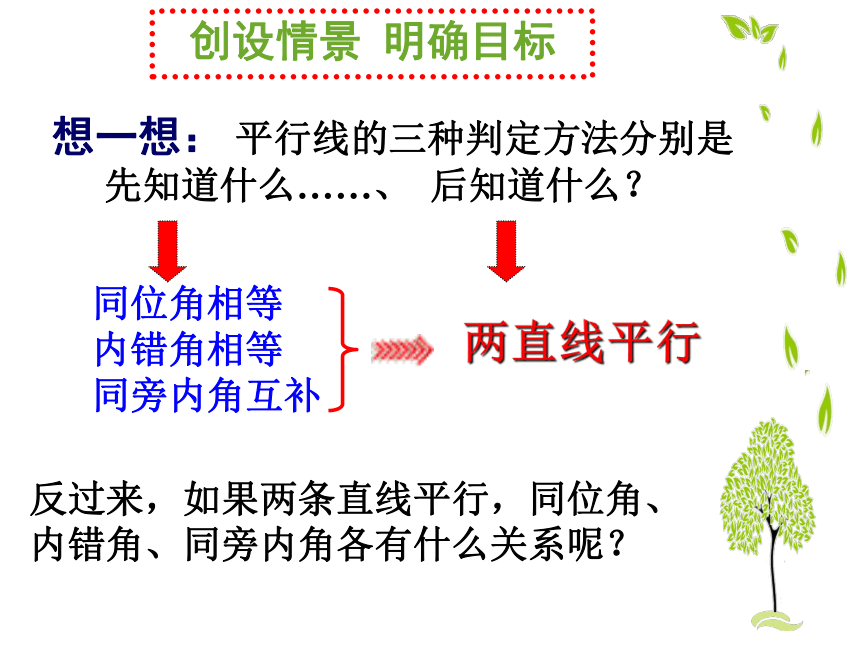
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
1
掌握平行线的性质并会熟练运用;
学 习 目 标
2
能够综合运用平行线的性质与判定进行推理。
合作探究 达成目标
探究点一:平行线的性质
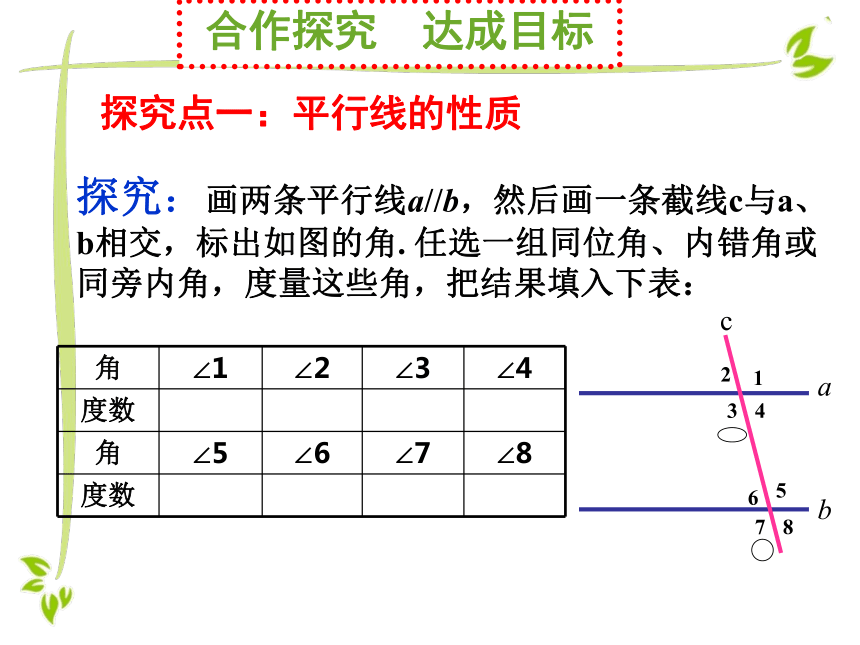
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
1
3
2
4
8
5
7
6
合作探究 达成目标
观察与猜想:
各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想:
猜想:
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____。
再任意画一条截线d,同样度量并计算各个角
的度数,你的猜想还成立吗?
相等
相等
互补
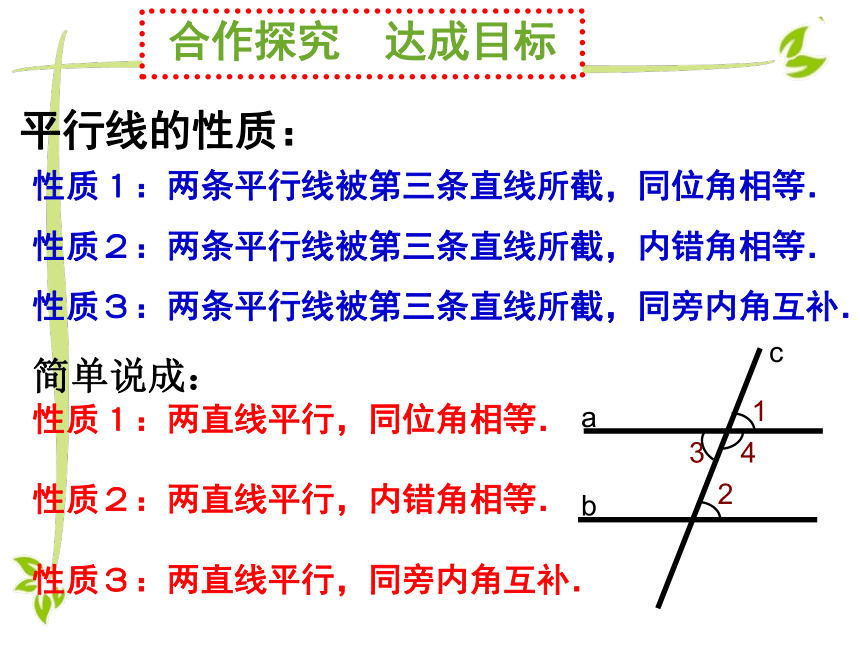
性质1:两条平行线被第三条直线所截,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
平行线的性质:
简单说成:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
a
b
c
1
2
3
4
合作探究 达成目标
合作探究 达成目标
探究点二:平行线的性质的应用
例 如图所示是一块梯形铁片的残余部分,量得∠A=100?, ∠B=115°,梯形另外两个角各是多少度?
D
A
C
B
解:∵梯形上下底互相平行
∴∠A与∠D互补,
∠B与∠C互补
∴∠C=180°-115°=65°
∴∠D=180°-100°=80°
总结梳理 内化目标
两直线平行
判定
性质
已知
得到
得到
已知
同位角相等
内错角相等
同旁内角互补
1.上交作业:教科书随堂练习;
2.课后作业: 见“学生用书”的当堂练习 .
课后作业
达标检测 反思目标
1.如图 (1)若AD∥BC,
则∠___=∠_____,
∠___=∠______,
∠ABC+∠_____=180°;
(2)若DC∥AB,则 ∠___=∠___,
∠___=∠___, ∠ABC+∠_____=180°.
5
1
8
4
BAD
3
7
2
6
BCD
达标检测 反思目标
2. 如图:AB∥CD ,∠ A=98°,∠C=75°,
则∠B=_____ 度,∠D=_____度
105
82
达标检测 反思目标
3.如图:AB∥CD,∠A=80°,∠B=60°,
则∠ACB=_____ 度.
40
达标检测 反思目标
4. 已知:如图.已知:AD∥BC,∠AEF=∠B
求证:AD∥EF.
证明:∵AD∥BC,(已知)
∴∠A+∠B=180°.
( )
∵∠AEF=∠B,(已知)
∴∠A+_______=180°,(等量代换)
∴ AD∥EF.
( )
两直线平行,同旁内角互补。
∠AEF
同旁内角互补,两直线平行。
1.上交作业:教材习题
2.课后作业:完成练习册
课后作业
2.3 平行线的性质
创设情景 明确目标
如图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( )
AB
CD
EC
BD
同位角相等,两直 线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
创设情景 明确目标
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
1
掌握平行线的性质并会熟练运用;
学 习 目 标
2
能够综合运用平行线的性质与判定进行推理。
合作探究 达成目标
探究点一:平行线的性质
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
1
3
2
4
8
5
7
6
合作探究 达成目标
观察与猜想:
各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想:
猜想:
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____。
再任意画一条截线d,同样度量并计算各个角
的度数,你的猜想还成立吗?
相等
相等
互补
性质1:两条平行线被第三条直线所截,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
平行线的性质:
简单说成:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
a
b
c
1
2
3
4
合作探究 达成目标
合作探究 达成目标
探究点二:平行线的性质的应用
例 如图所示是一块梯形铁片的残余部分,量得∠A=100?, ∠B=115°,梯形另外两个角各是多少度?
D
A
C
B
解:∵梯形上下底互相平行
∴∠A与∠D互补,
∠B与∠C互补
∴∠C=180°-115°=65°
∴∠D=180°-100°=80°
总结梳理 内化目标
两直线平行
判定
性质
已知
得到
得到
已知
同位角相等
内错角相等
同旁内角互补
1.上交作业:教科书随堂练习;
2.课后作业: 见“学生用书”的当堂练习 .
课后作业
达标检测 反思目标
1.如图 (1)若AD∥BC,
则∠___=∠_____,
∠___=∠______,
∠ABC+∠_____=180°;
(2)若DC∥AB,则 ∠___=∠___,
∠___=∠___, ∠ABC+∠_____=180°.
5
1
8
4
BAD
3
7
2
6
BCD
达标检测 反思目标
2. 如图:AB∥CD ,∠ A=98°,∠C=75°,
则∠B=_____ 度,∠D=_____度
105
82
达标检测 反思目标
3.如图:AB∥CD,∠A=80°,∠B=60°,
则∠ACB=_____ 度.
40
达标检测 反思目标
4. 已知:如图.已知:AD∥BC,∠AEF=∠B
求证:AD∥EF.
证明:∵AD∥BC,(已知)
∴∠A+∠B=180°.
( )
∵∠AEF=∠B,(已知)
∴∠A+_______=180°,(等量代换)
∴ AD∥EF.
( )
两直线平行,同旁内角互补。
∠AEF
同旁内角互补,两直线平行。
1.上交作业:教材习题
2.课后作业:完成练习册
课后作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
