人教版八年级数学上册:第十二章全等三角形精典专题——三角形辅助线总结
文档属性
| 名称 | 人教版八年级数学上册:第十二章全等三角形精典专题——三角形辅助线总结 |  | |
| 格式 | zip | ||
| 文件大小 | 73.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-06 00:16:07 | ||
图片预览

文档简介
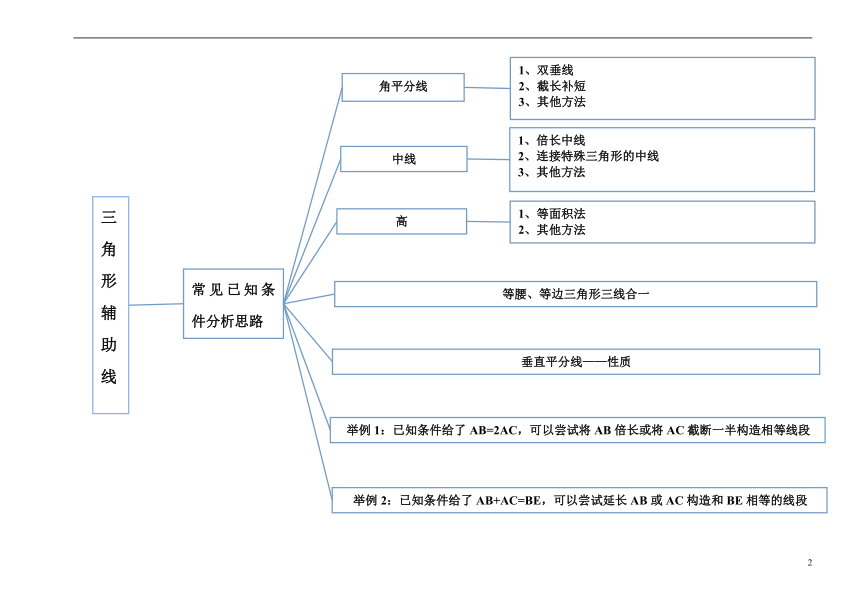
精典专题——三角形辅助线总结
精典例题分析示范
1、证明是等腰三角形
2、其他方法
在同一个三角形中
不在一个三角形中
证明角相等
三角形辅助线
1、证明是等腰三角形
2、其他方法
有公共顶点
无公共顶点
证明边相等
1、证明是等腰三角形
2、其他方法
1、全等
2、角平分线
3、八字形
4、同角的余角补角相等
5、利用平行
6、中垂线
7、其他方法
1、双垂线
2、截长补短
3、其他方法
角平分线
1、倍长中线
2、连接特殊三角形的中线
3、其他方法
中线
三角形辅助线
1、等面积法
2、其他方法
高
等腰、等边三角形三线合一
常见已知条件分析思路
垂直平分线——性质
举例1:已知条件给了AB=2AC,可以尝试将AB倍长或将AC截断一半构造相等线段
举例2:已知条件给了AB+AC=BE,可以尝试延长AB或AC构造和BE相等的线段
思路:可以考虑截长补短,利用三角形三边关系进行证明
证明:AB-AC>BD-DC
思路:可以截长补短或旋转构造相等线段
1、截长:在AF上截取与AD(或CF)相等的线段,利用全等证明剩下的线段与CF(或AD)相等
2、补短:通过旋转或延长AD(或CF)构造与AF相等得线段,证明延长的部分与CF(或AD)相等
3、
证明:AF=AD+CF
三角形辅助线
思路:
1、作∠CFD的角平分线,将∠CFD分成两个相等的角,证明其中一个与∠B相等
2、构造2倍∠CFD,证明其与∠B相等
常见证明结论思路
证明:∠CFD=∠B
思路:
1、找到DE中点,将DE分为两段相等的线段证明其一与AM相等
2、构造2倍AM证明其与DE相等(倍长中线)
证明:DE=2AM
思路:
利用截长在AD上截取一线段与OE相等
求AD-OE的值
例题分析1:如图,D为CE的中点,F为AD上一点,且EF=AC.求证:∠DFE=∠DAC.
思路1:(倍长FD),延长FD至FG,连接CG,证明△FDE≌△GDC,将∠DFE转移到∠DGC,利用EF=CG=AC证得∠DFE=∠DAC
思路2:(倍长AD),延长FD至FH,连接EH,证明△EHD≌△ADC,将∠DAC转移到∠EHD,利用AC=EH=EF证得∠DFE=∠DAC
思路3:过点E作EG⊥AD延长线于G,CF⊥AD于H,证明△ACH≌△GDE,再证明△HDC≌△FEG即可证得∠DFE=∠DAC
思路1:通过补短或倍长AE将AD+CF构造成一个线段GF
(本题中补短或倍长中线效果相同:有时不必刻意倍长,延长AE交BC于G点也是同样的效果,如果倍长AE于EG,还需要说明G在BC的延长线上):延长AE交BC于G点,证明△ADE≌△GCE,将AD转移至CG,将∠DAE转移至∠FGE,再利用∠DAE=
∠FAE=∠FGE证得AF=FG=AD+CF
思路2:由∠DAE=∠FAE可知AE平分∠DAF,利用角平分线的性质作垂线(类似于截长):过点E作EH⊥AF于点H,证明△ADE≌△AHE,再证明△EHF≌△ECF即可
例题分析2:如图所示,已知E为正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE.求证:AF=AD+CF.
