三年级上册数学奥数课件-第八讲 数阵图进阶 人教版(共13张PPT)
文档属性
| 名称 | 三年级上册数学奥数课件-第八讲 数阵图进阶 人教版(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-07 16:39:44 | ||
图片预览



文档简介
(共13张PPT)
第八讲
数 阵 图 进 阶
一、数阵图定义及分类:
定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.
数阵:是一种由幻方演变而来的数字图.
数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.
二、解题方法: 解决数阵类问题可以采取从局部到整体再到局部的方法入手:
第一步:区分数阵图中的普通点(或方格)和关键点(或方格);
第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系, 得到关键点上所填数的范围;
第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对 数学方法的综合运用.
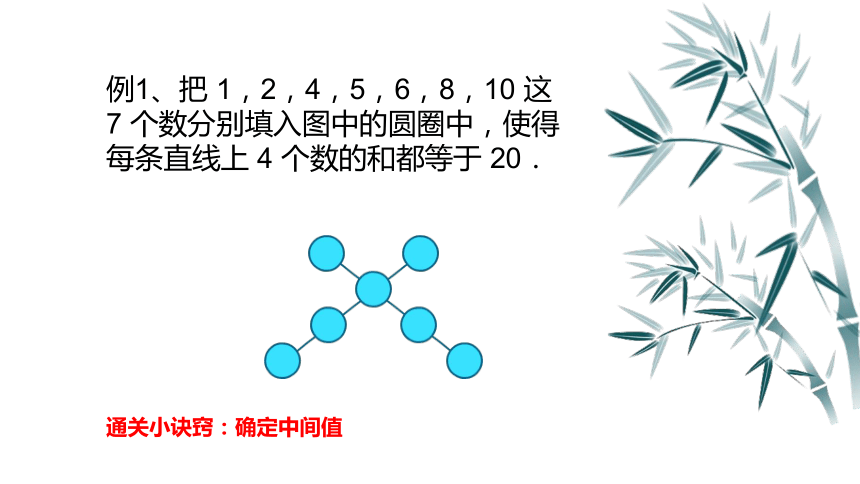
例1、把 1,2,4,5,6,8,10 这 7 个数分别填入图中的圆圈中,使得每条直线上 4 个数的和都等于 20.
通关小诀窍:确定中间值
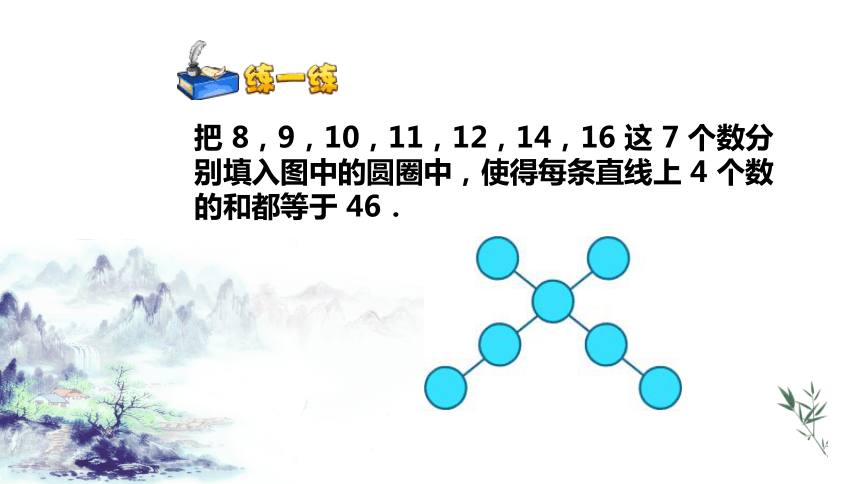
把 8,9,10,11,12,14,16 这 7 个数分别填入图中的圆圈中,使得每条直线上 4 个数的和都等于 46.
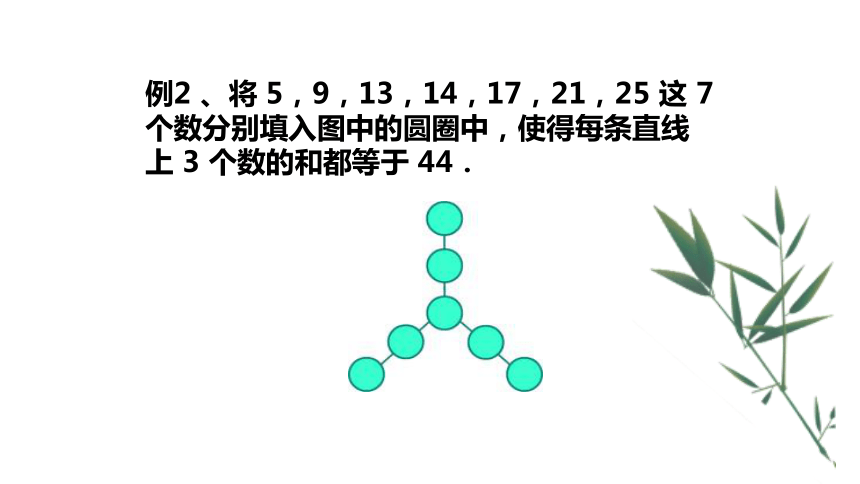
例2 、将 5,9,13,14,17,21,25 这 7 个数分别填入图中的圆圈中,使得每条直线上 3 个数的和都等于 44.
把1~11填入图中,使每条线上三个数的和相等.
例3、把 2,3,4,5,6,7,8 这七个数分别填入图中的圆圈中,使两个正方形中四个数之和都等于 19.
例4、 把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和是20。
将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
例5、把 1,5,9,10,16,21 这 6 个数分别填入图中的○里,使每一个大圆上的四个数之和都等于 36.
将 5,6,9,11,14,15 这 6 个数分别填入图中的圆圈里,使两个大圆上 4 个数的和都等于40.
把 1,3,4,5,6,8,11,15 这 8 个数分别填入图中的圆圈里,使得每个大圆上 5 个数的和都等于 33.
第八讲
数 阵 图 进 阶
一、数阵图定义及分类:
定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.
数阵:是一种由幻方演变而来的数字图.
数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.
二、解题方法: 解决数阵类问题可以采取从局部到整体再到局部的方法入手:
第一步:区分数阵图中的普通点(或方格)和关键点(或方格);
第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系, 得到关键点上所填数的范围;
第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对 数学方法的综合运用.
例1、把 1,2,4,5,6,8,10 这 7 个数分别填入图中的圆圈中,使得每条直线上 4 个数的和都等于 20.
通关小诀窍:确定中间值
把 8,9,10,11,12,14,16 这 7 个数分别填入图中的圆圈中,使得每条直线上 4 个数的和都等于 46.
例2 、将 5,9,13,14,17,21,25 这 7 个数分别填入图中的圆圈中,使得每条直线上 3 个数的和都等于 44.
把1~11填入图中,使每条线上三个数的和相等.
例3、把 2,3,4,5,6,7,8 这七个数分别填入图中的圆圈中,使两个正方形中四个数之和都等于 19.
例4、 把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和是20。
将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
例5、把 1,5,9,10,16,21 这 6 个数分别填入图中的○里,使每一个大圆上的四个数之和都等于 36.
将 5,6,9,11,14,15 这 6 个数分别填入图中的圆圈里,使两个大圆上 4 个数的和都等于40.
把 1,3,4,5,6,8,11,15 这 8 个数分别填入图中的圆圈里,使得每个大圆上 5 个数的和都等于 33.
